Verilen bir kesri sadeleştirmek basit bir işlem gibi görünür. Ancak özellikle ilköğretim düzeyindeki öğrencilerin sık yaptığı bir hata vardır. Bu hata, iki veya daha fazla basamaklı kesirlerin sadeleştirilmesi sırasında ortaya çıkar ve öğretmenlerin uyarısıyla sık sık düzeltilir. İlginç olan ise, bu yanlış yöntemin bazı örneklerde doğru sonuca ulaştırabilmesidir.
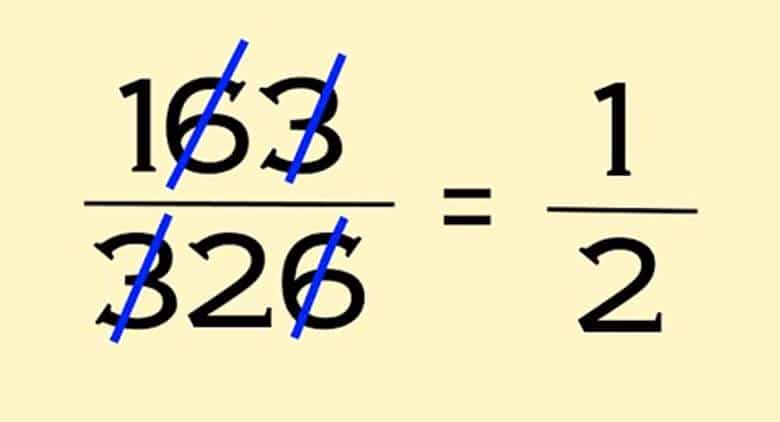
Örneğin 16/64 kesrini ele alalım. Matematik bilgisi sınırlı bir öğrenci, her iki taraftaki 6 rakamını sadeleştirerek 1/4 sonucunu bulabilir. Bu işlemin kurallara aykırı olduğunu biliyoruz. Ancak sonuç doğrudur. Bu, öğrenciye bir haklılık payı verir. Benzer durumlar 26/65 kesrinde 6’lar, 19/95 kesrinde 9’lar veya 49/98 kesrinde 9’lar için de geçerlidir.
Öğrenciler bu hatayı yapar ama bazen ulaştıkları doğru sonuç şans eseri değil, matematiksel bir gerçeklikten kaynaklanır. Yöntem hatalı da olsa belirli durumlarda doğru sonucu verir.
Ancak burada önemli bir nokta var. Hiçbir şekilde genelleme yapmamalıyız. Bazı örneklerde doğru sonuç vermesi, bu yöntemin her zaman geçerli olduğu anlamına gelmez. Eğer birkaç örneğe bakarak bunun genel bir kural olduğunu sanarsak önemli bir yanılgıya düşeriz. Şimdi, yukarıda aktardığımız hatalı yöntemle kesirleri sadeleştirirken sonucun neden bazen doğru çıktığını anlamaya çalışalım.
Kesirleri Yanlış Gidiş Yoluyla Doğru Biçimde Nasıl Sadeleştirdik?
Aslında iki basamaklı sayılarda bu durumun geçerli olduğu yalnızca dört örnek vardır. Bunlar, yukarıda da belirttiğimiz gibi 16/64, 26/65, 19/95 ve 49/98 biçimindedir. Şimdi bu durumu daha genel bir şekilde inceleyelim. Bu kesirler için elimizde xa ve ay biçiminde iki basamaklı sayılar varsa, şu eşitlik sağlanır:
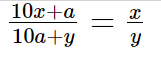
İçler dışlar çarpımı ve düzenleme ile yukarıdaki ifadeyi aşağıdaki biçimde de yazabiliriz.
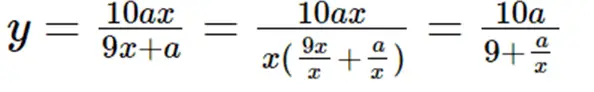
Bu noktada bu denklemi daha yakından inceleyeceğiz. Ele aldığımız kesrin payı ve paydası rakamlardan oluştuğu için x, y ve a’nın tamsayı değerler alması gerekiyor. Şimdi a/x oranını inceleyelim. Hangi sayıların bu koşulu sağladığını ve aynı şartı yerine getiren başka sayıların olup olmadığını anlamak için aşağıdaki tabloyu kullanarak durumu değerlendirelim.
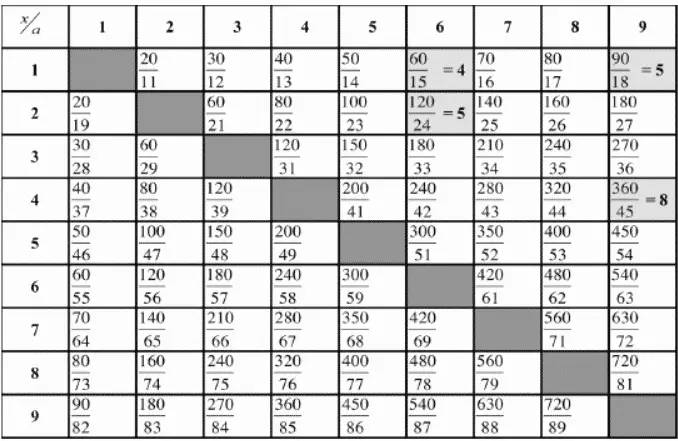
Yukarıdaki tabloda da görebileceğiniz gibi tüm x ve a sayıları yerlerine yerleştirildiğinde y’nin tamsayı olmasını sağlayan sadece 4 değer var. Bunlarda bizim en başta örnek olarak verdiğimiz sayılara denk geliyorlar.
Ancak bu nokta da aklınıza şu soru gelmelidir. İki basamaklı sayılar yerine daha fazla basamakla uğraşırsak acaba benzer kazara doğru sonuçlar bulabilir miyiz? Cevabımız bir kere daha evet. Hatalı da olsa doğru cevap veren bu sayıları aşağıda görebilirsiniz.
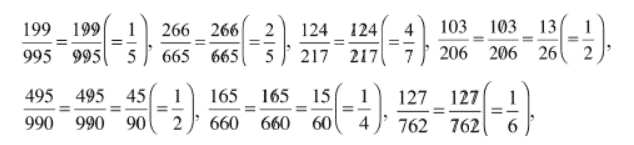
Ayrıca aşağıdaki kesirlerin de hepsi birbirine denktir ve başlangıçtaki kesir bizim iki basamaklı sadeleşen sayımız olduğu için bu sayılarda, tekrar eden rakamları silmeniz sonucunda sadeleşebilmekte ve yine doğru cevabı vermektedir.

Kesirleri Bu Biçimde Sadeleştirmeyi Lütfen Sadece Eğlence Amaçlı Kullanınız
Bir kere daha hatırlatalım. Aktardığımız bilgiler bir kural teşkil etmez. Sadece matematiğin ve sayıların eğlenceli yüzünü bizlere gösterir. Bu nedenle sınıflarda eğlenceli bir aktivite olarak kullanılmalı ve bunun bir hata olduğu vurgulanmalıdır. Bu tuhaf kesirlerden bir kaç örnek daha verelim sizlere. Hepsini sadeleştirmek için kullanılan gidiş yolu yanlış ancak yine de sonuçları doğrudur!

Matematik hataların içinde de keşfedilmeyi bekleyen hazineler mevcuttur. Bu hazineleri keşfetmek de eğlencelidir. Ayrıca göz atmak isterseniz: Ondalık Sayılar Neden Bazı Ülkelerde Nokta Bazılarında İse Virgül İle Gösterilir?
Kaynaklar ve ileri okumalar:
- Magnificent mistakes in mathematics / by Alfred S. Posamentier and Ingmar Lehmann,2013; Prometheus Books
- The Wrong Way To Reduce Fractions. But It Works Sometimes; Yayınlanma tarihi: 8 Aralık 2014; Bağlantı: https://www.youtube.com/watch?v=fQl040dANZw
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





