Hesaplamaları yaparken, bir problem çözerken hepimiz matematik hataları yaparız. Buna bir çözüm olarak da elektronik hesap makineleri hassastır ve asla hata yapmazlar diye düşünürüz. Ancak, aslında hesap makineleri de hata yapar.

Tarihteki meşhur matematik hatalarına göz atmadan önce bir hesap makinesinin nasıl hata yapabileceğini sizlere gösterelim. Bunun için bir hesap makinesine ihtiyacınız var. İki işlem kullanacaksınız. Kare alma ve kök alma.
Şimdi şu prosedürü izleyin: 10 rakamına, ardından karekök düğmesine ve ardından kare düğmesine basın. Bu iki işlem birbirinin tersi olduğu için ekranda 10 rakamının belirmesi fazla şaşırtıcı bir sonuç değil. Şimdi şunu deneyin: 10 rakamına basın, ardından karekök düğmesine 25 kez ve kare düğmesine 25 kez basın. Beklenen sonuç yine 10 olmalıdır, ancak ekran 9.9999997 gibi bir şey görüyor olmanız muhtemeldir.

Normalde, bu oldukça küçük bir sapma ama bir gariplik olduğunu fark etmeniz lazım. Eğer sıkılmadıysanız bu sefer 28 defa aynı şeyi deneyin. Gerçek sayı ile hesap makinesi tarafından hesaplanan sayı arasındaki farkın giderek büyüdüğünü fark edeceksiniz.

Her dijital hesap makinesinde şu ya da bu şekilde ortaya çıkan bu sonucun aslında fazla şaşırtıcı yanı yoktur. Sonuçta kullandığımız sayı irrasyonel bir sayıdır. Yani sayı sonsuz sayıda basamağa sahiptir. Ancak hesap makineleri yalnızca sınırlı sayıda sayıyı depolar. Sayısal değerler bilgisayarlar tarafından genelde 15 basamaktan sonra kesilir.
Bu nedenle, gerçek sayılar ile saklanan veya görüntülenen değerler arasında çok küçük hatalar vardır. Ancak bizler gündelik yaşantımızda ondalık sayıların genelde virgülden sonraki ilk iki basamağı ile idare edebildiğimiz için bu hatanın farkına varmayız. Bu ön bilginin devamında bazı sorun çıkaran matematik hatalarına göz atabiliriz.
Mars Climate Orbiter Yörünge Hatası
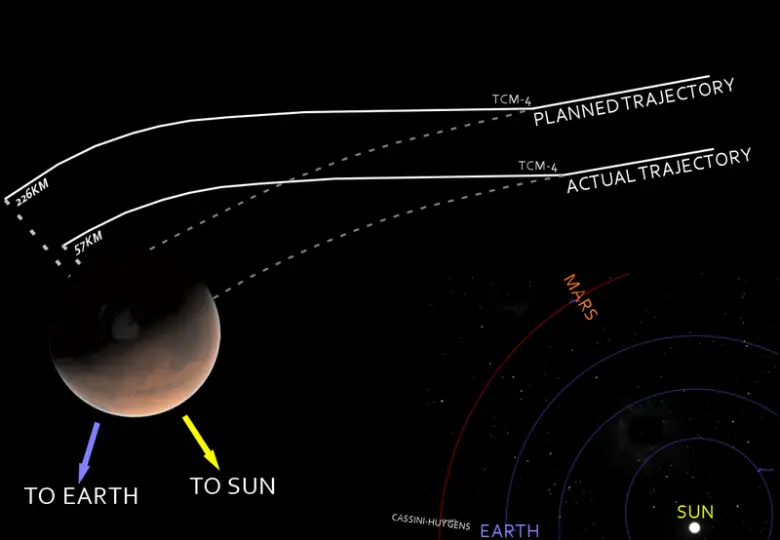
Amerikalıların ölçü birimlerini birbirine çevirirken yaptıkları hatalar ile ilgili bir çok örnek vardır. Bu konuya en güzel örnek Mars Climate Orbiter’da yaşandı. 11 Aralık 1998 tarihinde Mars Climate Orbiter Mars yolculuğuna çıktı. Bu uzay aracı kırmızı gezegenin keşfinde önemli bir rol oynayacaktı.
23 Eylül 1999’da uzay aracını yörüngeye yerleştirmek için son roket fırlatıldı. Ancak her roket fırlatılışında yapılan bir matematik hatası nedeniyle uzay aracı yörüngesinden şaştı. Bu araç, yaklaşık 10 aylık seyahatin ardından 669 milyon kilometre mesafe kat ederek Mars’a ulaşacak ve kırmızı gezegenin benzersiz iklimini gözlemleyecekti. Ancak mühendisler İngiliz ölçü birimlerini metrik ölçü birimlerine dönüştürürken bu hatayı yapmışlardı.
NASA’nın yazılımı libre (pound) cinsinden gelen sayıları Newton biriminde varsayarak işlem yaptı. Bu nedenle uydunun iticileri için gereken kuvvet değerleri yanlış hesaplandı. Bu hata Mars keşif aracımızın gezegenin atmosferine düşük bir irtifada girmesine ve sonrasında da büyük ihtimalle atmosfer sürtünmesinden dolayı yanarak parçalanmasına neden olmuştu.
Aracın geliştirilmesi, iniş aracı ve görev için gerekli insan kaynağının maliyeti 327,6 milyon dolardi. Bu, bilimsel açıdan hiç bir getirisi olmayan, ancak geliştirilen yazılımların denetlenmesinin önemine müthiş bir örnek olarak kayda geçen bir harcama oldu.
Amsterdam Belediye Meclisinin 188 Milyon Euro’luk Konut Yardımı Hatası

2014 yılında Amsterdam, euro yerine sent cinsinden programlanan yazılımı kullandığında, yoksul ailelere 1,8 milyon euro yerine 188 milyon euro gönderdi. Yani bir kişiye 155 euro vermeyi planlarken bunun yerine 15.500 euro gönderildi.
Hükümet daha sonra bir hesaplama hatası yaptığını fark etti ve fazladan yolladığı paranın iadesini istedi. İşin ilginç tarafı bir çok kişi kendisine ödenen fazla parayı da iade etti. Yanlış ödemelerden kaynaklanan 188 milyon Euro’nun 2,4 milyon Euro’su hariç tamamı geri alındı.
Laufenberg Köprüsü Sorunu

Almanya ve İsviçre şehirlerini birbirine bağlayacak Laufenburg isimli köprü, Ren Nehri üzerinde inşa edilmeye başlanmıştı. Anlaşma gereği iki ülke, nehrin kendi taraflarında kalan bölgeden inşaata başlayacak ve köprü ortada birleştirilecekti. 2003 yılında, köprünün bir yarısının diğerinden 54 santimetre daha yüksek olduğunu fark edildiğinde, köprü neredeyse bitmek üzereydi.
Hata, ülkelerin deniz seviyesi tanımının birbirinden farklı olmasından kaynaklanmıştı. Çoğu ülke, her yerde aynı olmadığını göz önünde bulundurarak deniz seviyesini belirlemek için farklı yöntemlere sahiptir. Almanya deniz seviyesini belirlemek için Kuzey Denizi’ni kullanırken, İsviçre Akdeniz’i tercih eder. Bu hespalama biçimleri de 27 cm lik bir farka denk gelir. Almanya ve İsviçre elbette başlangıçta bunu biliyorlardı ve bunu hesaplamalarına dahil etmişlerdi. Ancak hatayı düzeltmekle yükümlü olan kişi bu farkı silmek yerine ikiye katlamıştı. Köprünün tamamlanabilmesi için Almanya’ya ait kısmının alçaltılması gerekmişti. Sonuçta da görselde gördüğünüz köprü ortaya çıktı.
1628 Vasa Savaş Gemisinin Batışı

1628’de İsveçliler yeni bir savaş gemisi olan Vasa’nın ilk yolculuğunda kısa süre içinde batmasını ve içindeki 30 kişinin ölümüyle dehşet içinde izledi. 1626 yılında İsveç Kralı II. Gustavus Adolphus’un emriyle inşa edilmeye başlanan gemi, Kuzey Avrupa’da güçlü bir deniz gücü oluşturma çabasının bir parçasıydı. Vasa’nın tasarımı oldukça iddialıydı, zengin süslemelerle bezenmişti ve oldukça yüksek bir silah gücüne sahipti.
64 bronz topla donanmış olan bu gemi, bazıları tarafından dünyanın en güçlü savaş gemisi olarak görülüyordu. Ancak, Vasa’nın inşası sırasında yaşanan bazı tasarım ve mühendislik hataları, geminin dengesiz olmasına neden oldu.
Geminin kalıntılarını inceleyen uzmanlar, geminin asimetrik olduğunu, iskele tarafının sancak tarafına göre daha kalın olduğunu söylüyor. Bunun nedeninin işçilerin farklı ölçüm sistemleri kullanıyor olması olduğu tahmin ediliyor. Arkeologlar gemiyi inşa eden işçilerin kullandığı dört cetvel buldular. Bunlardan ikisi 12 inçlik İsveç ayağıyla kalibre edilirken, diğer ikisi 11 inçlik Amsterdam ayağıyla ölçülmüştü.
İspanya’nın S-80 Denizaltı Programı

İspanya, 2003 yılında İspanya donanması için dört dizel denizaltı inşa etmek üzere 2.7 milyar dolarlık S-80 denizaltı programını başlattı. İspanya, denizaltılardan birini 2013 yılında tamamladı, ancak ortada çok büyük bir sorun vardı. Tamamlanan denizaltı, olması gerekenden 70 ton daha ağırdı. İspanya donanması, bu denizaltının denize daldığında asla su yüzüne çıkamayacağını açıkladı.
Denizaltı projesinde çalışan bir mühendis, hesaplamalar esnasında bir sayının basamaklarından sonra koyması gereken virgülü, bir basamak kaydırmıştı. Ancak daha komik olan ise, ilk denizaltı tamamlanana kadar kimse bu hatayı fark etmemişti.
Hatanın keşfedildiği sırada, diğer 3 denizaltı da yapım aşamasındaydı. S-80 denizaltılarının 2015 yılında hizmete girmesi planlanıyordu. Ancak bu hata 7 yıllık gecikmeye neden olacaktı. Sorunu düzeltmek için yaklaşık 2 milyar Euro harcandı. Bu da tarihteki en pahalı matematik hatalarından biri olarak akıllarda kaldı.
Bazı Matematik Hataları Sürpriz Sonuçlara Sebep Oldu

Bununla birlikte, matematik hataları önemli bir keşfe yol açtı. 1960’larda bir gün, Massachusetts Teknoloji Enstitüsü’nde bir meteorolog olan Edward Lorenz, bilgisayarında hava simülasyonlarını gözlemlemekle meşguldü. Bir süre sonra ara vermeye karar verdi. Lorenz programı çalıştırmayı bıraktı ve ara sonuçları not etti.
Kahvesini bitirdikten sonra Lorenz masasına döndü, sonuçları bilgisayara geri verdi ve simülasyonu çalıştırdı. Ancak bilgisayarındaki hava durumu, önceki simülasyonlarda gözlemlediğinden farklı sonuçlar veriyordu.
Kahve almaya gitmeden önce ekranında gördüğü sayıları kopyalamıştı. Bu sayılar, virgülden sonraki üç basamağı gösteriyordu. Ancak bilgisayarın içinde sayılar sekiz ondalık basamağa kadar saklanıyordu. Lorenz son üç sayıyı bilgisayara girdiğinde sistem başka bir biçimde çalışmaya başlamıştı.
Hava simülasyonu hesaplaması, doğrusal olmayan işlemler içerdiğinden, şaşırtıcı farkın ortaya çıkması normaldi. Doğrusal olmayan ifadeler – yani kare alma veya karekök alma gibi ifadeler – çok hızlı bir şekilde küçük hataları bile büyütme gibi can sıkıcı özelliklere sahiptir. Edward Lorenz’in keşfi, kaos teorisinin temelini oluşturdu.
Kaynaklar ve ileri okumalar
- George G. Szpiro; The Secret Life of Numbers: 50 Easy Pieces on How Mathematicians Work and Think; ISBN: 0-309-65958-2
- 10 Simple But Costly Math Errors In History. Yayınlanma tarihi: 30 Ağustos 2019. Bağlantı: https://listverse.com/
- Mars Probe Lost Due to Simple Math Error; Yayınlanma tarihi: 1 Ekim 1999. Bağlantı: https://www.latimes.com/
- Clyde Tombaugh: Astronomer Who Discovered Pluto; https://www.space.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










