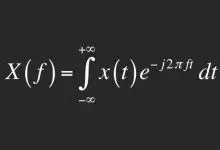Yanlış bilgi söz konusu olduğunda, “viral olmak” basit bir slogan olmaktan daha fazlası gibi görünüyor. Bilim insanları yanlış bilginin yayılması ile virüslerin yayılması arasında yakın bir benzerlik buldular.

Yanlış bilginin yayılımını, patojenlerin yayılmasını simüle etmek için tasarlanmış matematiksel modeller yardımı ile açıklamak mümkündür. Epidemiyolojide (hastalıkların toplumda nasıl ve neden ortaya çıktığının incelenmesi) kullanılan matematiksel modeller, virüslerin yayılmasını incelemek için geliştirilmiştir. Ancak sosyal ağlarda yanlış bilginin yayılmasını incelemek için de kullanılması mümkündür.
Hastalığın yayılmasının matematiksel modellemesinin en eski hesabı 1760 yılında Daniel Bernoulli tarafından yapılmıştır. Daha yakın zamanlarda ise Kermack–McKendrick salgın modeli (1927) ve Reed–Frost salgın modeli (1928), gibi modeller ortaya atılmıştır. Bunlardan birisi de SIR (Susceptible-Infected-Recovered) modelidir.
SIR Modeli Nedir?
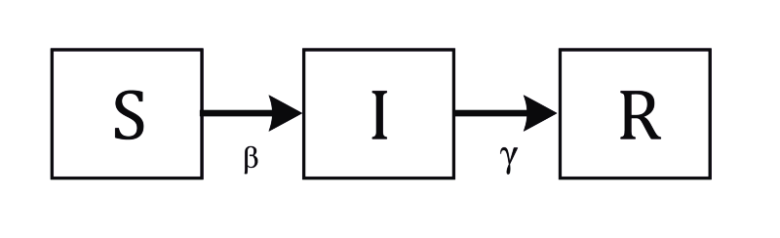
- S (Susceptible): Hastalığa karşı duyarlı, yani enfekte olmamış ancak enfekte olma riski olan bireyler.
- I (Infected): Hastalığa yakalanmış ve bulaştırıcı durumda olan bireyler.
- R (Recovered): Hastalığı geçirip iyileşmiş, artık bağışıklık kazanmış ve tekrar bulaşıcı olamayan bireyler (veya ölüm durumunda artık bulaştırıcı olmayanlar).
SIR modeli, bireylerin bu üç grup arasında nasıl hareket ettiğini modelleyerek hastalığın yayılımını simüle eder. Duyarlı bireyler (S) enfekte bireylerle (I) temas ettikçe hastalığa yakalanma riski taşır. Enfekte bireyler (I) bir süre sonra iyileşerek ya da bağışıklık kazanarak (R) grubuna geçiş yapar.
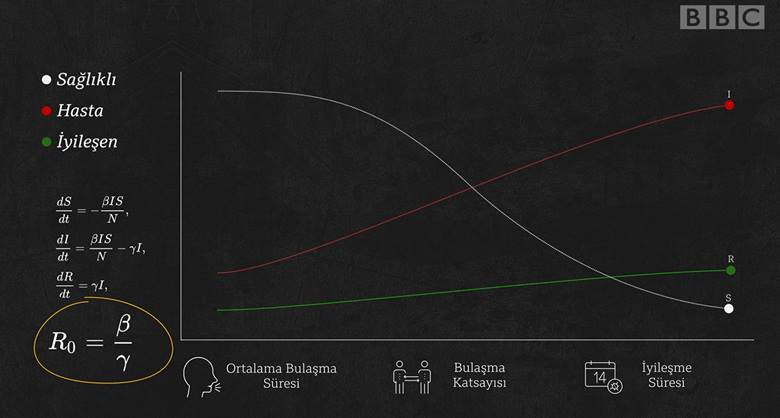
Bu modelde β (beta) bulaşma hızı ve γ (gamma) iyileşme hızı olmak üzere iki parametre vardır.
- Bulaşma hızı (β), bir enfekte bireyin duyarlı bir bireye hastalığı bulaştırma olasılığını belirler.
- İyileşme hızı (γ), enfekte bireylerin iyileşip bağışıklık kazanarak iyileşmiş grubuna geçiş hızıdır. Bu model, diferansiyel denklemler aracılığıyla aşağıdaki gibi ifade edecektir.
Sosyal medyada yanlış bilgi, hastalıklar gibi, bireyden bireye yayılacaktır. Bunun sonucunda bazıları enfekte olur, bazıları bağışıklık kazanır. Bazıları da sadece hastalık taşıyıcıları olarak hizmet eder, bilmeden veya bundan olumsuz etkilenmeden yanlış bilgi yayarlar. Örneğin, büyük takipçi kitlesine sahip önde gelen sosyal medya figürleri süper yayıcılar ” haline gelebilir ve potansiyel olarak yüz milyonlarca insana yalnlış bilgi yayarlar.
Yanlış Bilgiyi Önceden Tespit Etmek Psikolojik Aşılamaya Benzer
Yanlış bilginin yayılmasını virüs yayılımına benzetmek, bilim insanlarının bu yayılımı önlemenin yollarını simüle etmesine olanak sağlar. Bu müdahaleler arasında “psikolojik aşı” adı verilen bir yaklaşım bulunur.
Bu yöntemde araştırmacılar, insanların yanlış bilgiye karşı bağışıklık kazanmasını sağlamak için, yanlış bir bilgiyi önceden sunar ve sonra bunu çürütürler. Bu, insanlara virüsün zayıflatılmış bir dozunun verildiği ve bağışıklık sisteminin sonraki karşılaşmalara hazırlanmasını sağlayan aşılamaya benzer bir süreçtir.
Aşağıdaki grafikte, eğer önceden çürütme uygulanmazsa, insanların yanlış bilgiye karşı bağışıklık kazanmasının çok daha uzun sürdüğünü görebilirsiniz (sol panel, turuncu çizgi). Sağ panel, önceden çürütmenin büyük ölçekte uygulanması durumunda, yanlış bilgilendirilen insanların sayısını nasıl sınırlayabileceğini göstermektedir (turuncu çizgi).
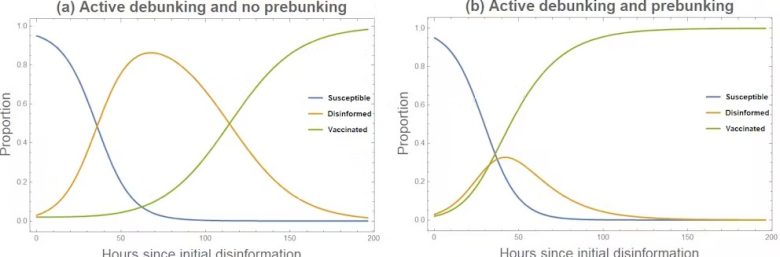
Bu modellerin amacı, sorunun korkutucu görünmesini sağlamak veya insanların her şeye inanan birer taşıyıcı olduklarını ima etmek değildir. Ancak bazı sahte haberlerin, kullanıcıları anında “bulaştırarak” basit bir salgın gibi yayıldığına dair net kanıtlar vardır. Bu arada, bazı yanlış bilgi türleri ise daha karmaşık bir salgın gibi davranır; burada insanların “enfekte” olmadan önce yanıltıcı kaynaklarla tekrar tekrar karşılaşmaları gerekir.
Sonuç Olarak
SIR modeli, bir popülasyondaki salgın hastalıkların yayılımını tahmin etmekte yararlıdır. Ancak, model bazı varsayımlara dayanır. Örneğin herkesin hastalığa eşit derecede duyarlı olduğu kabul edilmektedir. Ayrıca popülasyonun toplam sayısının sabit olduğunu (doğum, ölüm, göç olmadığını) varsayar. Bu basitleştirmeler nedeniyle SIR modeli gerçek dünyadaki bazı durumlardan sapacaktır. Ancak yine de çoğu durumda doğru yaklaşımlar geliştirilmesini sağlar.
Sahte haberlerin incelenmesine epidemiyolojik bir yaklaşım benimsemek, yayılmasını tahmin etmemize ve önceden çürütme gibi müdahalelerin etkinliğini modellememize olanak tanır. Modeller asla mükemmel değildir. Ancak yanlış bilginin yayılmasını durdurmak istiyorsak, toplumsal zararlarına etkili bir şekilde karşı koymak için onu anlamamız gerekir.
Kaynaklar ve ileri okumalar
- Misinformation really does spread like a virus, suggest mathematical models drawn from epidemiology. Yayınlanma tarihi: 5 Kasım 2024. Kaynak site: Conversation. Bağlantı: Misinformation really does spread like a virus, suggest mathematical models drawn from epidemiology
- Bak-Coleman JB, Kennedy I, Wack M, Beers A. Schafer JS, Spiro ES, Starbird K, West JD. Combining interventions to reduce the spread of viral misinformation. Nat Hum Behav. 2022 Oct;6(10):1372-1380. doi: 10.1038/s41562-022-01388-6. Epub 2022 Jun 23. PMID: 35739250; PMCID: PMC9584817.
- Tolles J, Luong T. Modeling Epidemics With Compartmental Models. JAMA. 2020 Jun 23;323(24):2515-2516. doi: 10.1001/jama.2020.8420. PMID: 32459319.
- New mathematical models may help us predict the spread of future epidemics. Yayınlanma tarihi: 12 Nisan 2020. Bağlantı: New mathematical models may help us predict the spread of future epidemics/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel