Bizi ve dünyayı birbirine bağlayan, dünyayı bambaşka görmemizi sağlayan bazı matematiksel bağlantılar vardır. Bunlardan bir tanesi de Benford yasasıdır.

Şimdi hemen etrafınıza bakın ve üzerinde bol miktarda sayı bulunan bir şey bulmaya çalışın. Bu bir gazete, gelir giderlerinizi yazdığınız defteriniz, kısacası bolca sayı içeren herhangi bir şey olur. Şimdi de bulduğunuz sayıları incelemeye başlayın.
Yapmanız gereken sadece sayının başlangıç basamağına bakmak. Sıfır ile başlayanları hesaba katmayın. Şimdi kaçının 1 sayısı ile kaçının 2 sayısı ile, kaçının 3 sayısı ile vb. başladığını sayın. Bulduğunuz sonuçları bir yere yazın. Ne fark ettiniz?
Normal koşullarda her rakamın görülme ihtimalinin diğerleri ile aynı olduğunu düşünebilirsiniz. Başka bir deyişle, bir gazeteden rastgele alınan bir sayının 9’la olduğu kadar 1 ile başlamasının eş olasılıkta olmasını bekleyebilirsiniz. Ne var ki çoğu veri türü için bu düşüncenin aslında yanlış olduğunu biliyoruz. Aslında, sayıların neredeyse yarısı 1 veya 2 ile başlayacaktır. Sonrasında da rakam 9’a doğru gittikçe görülme olasılığı azalacaktır.
Benford Yasası Nedir?
Bu durum size basit bir gözlem gibi görünebilir, ancak Benford yasası, insanları parmaklıklar ardına koymak ve büyük dolandırıcılık operasyonlarını tespit etmek için kullanılmıştır.

Rakamların dağılımının eşit olmaması ile ilgili bu durumu 1881 yılında ilk fark eden kişi, bir matematikçi ve astronom olan Simon Newcomb’du. Newcomb bazı hesaplamalar için bir logaritma kitabı kullanıyordu. Ancak kitabın ilk sayfalarının daha fazla yıpranmış olduğunu gözlemledi. Bazı nedenlerden dolayı, insanlar sürekli olarak belirli sayıları diğerlerinden daha sık arıyor gibiydi.
Muhtemelen Newcomb da az evvel sizin yaptığınız gibi oturup saymıştı. Sonrasında yaptığı çalışmalar sonucunda bir formüle ulaştı. N rakamı ile başlayan sayıların yüzdesinin log (N + 1) – log (N) kadar olduğunu ileri sürdü. Ancak Newcomb, bulgusu için herhangi bir açıklama yapmadı. Bunun sonucunda da bu açıklaması elbette unutuldu gitti.
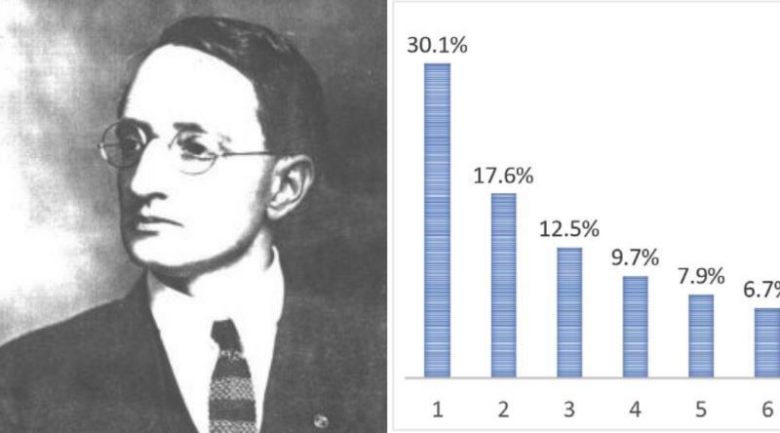
Yaklaşık 50 yıl bu gözlemle ilgili pek bir çalışma yapılmadı. Daha sonra 1939 yılında General Electric’de bir mühendis olan Frank Benford, ilginç bir gözlem yaptı. Şehirlerin nüfus istatistiklerine bakarken, sayıların çok daha fazlasının “1” ile başladığını fark etti.
Bu keşiften büyülenen Benford, gerçek dünyadaki sayıların buna ne kadar uygun olduğunu görmek için yola çıktı. Hisse senedi fiyatlarına, nehir uzunluklarına, spor istatistiklerine ve daha bir çok sayı koleksiyonuna baktığında aynı şaşırtıcı sonuç ile karşılaştı.
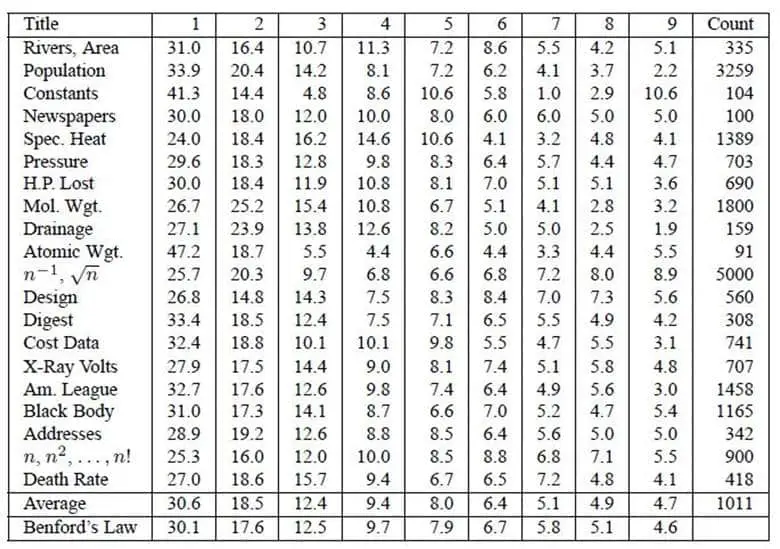
Sonucunda ilk rakamın belirli bir değeri alma olasılığının 1’den 9’a doğru rakam arttıkça azaldığını ortaya koydu. Benford bulduğu formüle Anormal Sayılar Kanunu adını verdi. Ancak bugünlerde adı Benford Yasası olarak bilinmektedir. Analizi, yasanın varlığının kanıtıydı, ancak Benford da bunun neden böyle olması gerektiğini tam olarak açıklayamadı.
Neden Benford Yasası Her Yerde Karşımıza Çıkıyor?
Aslında bu sorunun cevabını vermek kolay değil. Bu ilginç ilişkiyi açıklamaya yönelik ilk adım, 1961’de New Jersey’li bir matematikçi olan Roger Pinkham’dan geldi. Bu yasanın evrensel olup olmadığını anlamak o da çeşitli sayı kümeleri ile çalışmalar yaptı. Sonucunda nehir uzunluklarından tutun da, galaksilerin uzaklıklarına kadar çok çeşitli veri kümelerinin hepsinde yasanın geçerli olduğunu gösterdi.
Fenomen 1995 yılında, Theodore P. Hill tarafından tekrar incelendi. Benford Yasasını izleyen veri serilerindeki sayıların aslında “ikinci nesil” dağıtımlar olduğu, yani diğer dağıtımların kombinasyonları olduğu ortaya konuldu.
Sayılar Yardımı İle Dolandırıcılık Tespiti
Mali verilerin de Benford Yasasına uyduğunu anladığımız zaman bu sayı dizilimine olan ilgi daha da artacaktı. önemi büyüktür. Bu da yine bir tesadüf sonucunda olacaktı.

Muhasebe alanında öğretim görevlisi olan Mark Nigrini, öğrencilerinden, ilk rakamların tahmin edilebilir dağılımını kendilerine göstermek için bildikleri bir işletmenin hesaplarına bakmalarını istedi. Bir öğrenci, bir nalbur dükkanı işleten kayınbiraderinin hesaplarına bakmaya karar verdi. Şaşırtıcı bir şekilde, sayılar Benford dağılımına hiç benzemiyordu. Tutarsızlık o kadar büyüktü ki, rakamlar bir şeylerin yanlış olması gerektiğini gösteriyordu. Bu öğrenci farkında olmadan bir sahtekarlığı açığa çıkarmıştı.
Sonuçta bir kişi vergi beyannamelerini tahrif etmeye çalışırsa, o zaman bazı verileri değiştirmek ve yenilerini eklemek zorunda kalacaktır. Bu yasanın doğal biçimde ortaya çıkan dağılımlarda geçerli olduğunu hatırlatalım. Bu nedenle bir düzenbazın aynı doğallıkta sayı eklemesi mümkün olamaz.
Bu küçük başlangıçlardan itibaren, Benford Yasası, birçok muhasebecinin dolandırıcılığı tespit etmek için kullandığı resmi araçlardan biri haline geldi. Örneğin yasa, 2001 yılında Yunanistan’ın ekonomik verilerini incelemek için kullanıldı. Sonrasında ülkenin Avrupa Birliği’ne katılmak için sayıları manipüle ettiği anlaşıldı. Günümüzde bu yasa sahte haber ve görüntüleri tespit etmek için de kullanılmaktadır.
Dijital fotoğraflar da temelde sayılardan oluşur. Bu görüntüleri kurcalarsanız bu sayılar Benford yasasına uygunluklarını yitirir. Aslında bunun arkasındaki mantık açıktır. Organik süreçler küçük rakamları tercih eden sayılar üretir. Ancak verileri tahrif etmeye yönelik yöntemler bunu yapmaz.
Benford Yasası Nasıl Çalışıyor?
Yazıyı bu noktaya kadar okuduysanız Benford Yasasının neden her yerde karşımıza çıkıyor olduğunu merak etmiş olmalısınız. Aslına bakarsanız her dağılım Benford yasasına uymaz ve bunun mantığı çok basittir. Örneğin ayakkabı numaralarını ele alalım. Türkiye’deki insanların ayakkabı numaralarını inceleyen bir istatistiği incelerseniz Benford yasasının uygun olmadığını görürsünüz. Yani sayılar ile ilgili her yerde karşımıza bu örüntü çıkar biçiminde bir iddia doğru değildir.
Bu yasanın nasıl çalıştığını anlamak için bir şapkadan rastgele bir sayı çekeceğiniz bir çekiliş hazırladığınızı hayal edin. Elinizde sadece 1, 2, 3, 4 numaralı dört çekiliş bileti olsun. Kazanan numaranın 1 ile başlama şansı nedir? Tabii ki 4’te 1 veya yüzde 25. Şimdi 5, 6, 7 gibi daha fazla çekiliş biletini dahil edelim. 9 bilet için her birinin çekilme olasılığı 9’da 1 yani % 11’e düşecektir.
Ancak, 10 numaralı bileti eklediğinizde işler değişir. On biletten artık ikisi 1 (yani 1 ve 10) ile başlıyor. Bu nedenle biletin ilk sayının 1 ile başlama olasılığı yüzde 20 çıktı. Sonucunda 11, 12, 13… 19’a kadar bilet sattıkça artmaya devam edecek ve ilk 20 bilette oran 11 ⁄ 19 veya yüzde 58’e ulaşacaktır. Ancak 20’ler, 30’lar ve üzerini ekledikçe, ilk sayının 1 olma şansı tekrar düşer.
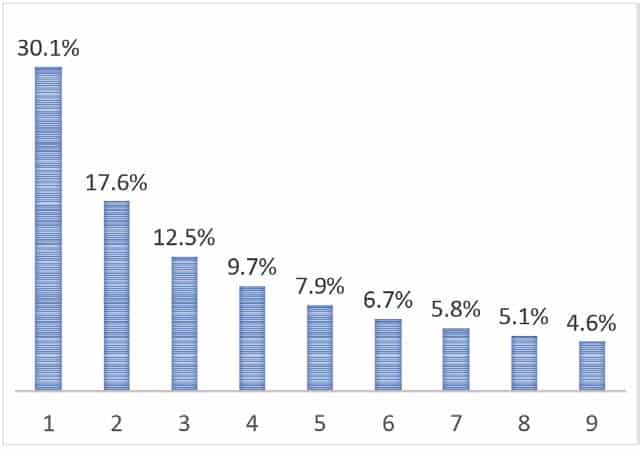
Aslında 1’den 99’a kadar sayılarda ilk sayının bir olma olasılığı 11 ⁄ 99 yani yaklaşık yüzde 11 kadardır. Peki ya 100’den fazla sayı koyarsanız? Şansınız bir kez daha artar. 199. çekiliş biletine ulaştığınızda, kazanan biletin ilk basamağının 1 olma şansı 111 ⁄ 199. Yani bir kez daha yüzde 50’nin üzerindedir.
Benford Yasasına Göre Sayıların Görülme Sıklıkları
İlginç bir şekilde, satılan bilet sayısı arttıkça şans yüzde 58 ile yüzde 11 arasında zikzaklar çizer. Sonunda kaç tane satılacağını bilemezsiniz. Ancak Benford Yasasının öngördüğü gibi, “ortalama” şansın bu ikisinin ortasında bir yerde olacağını görebilirsiniz. Bir sayının Benford Yasası tarafından öngörüldüğü gibi N rakamıyla başlama olasılığı başta da dediğimiz gibi log (N + 1) – log (N) kadardır. N = 1 için bu, log (2) – log (1) veya yüzde 30,1 olan 0.301’e denk gelir.
Günümüzden 150 yıl önce bir adamın bir kütüphane kitabında fark ettiği basit bir gözlem günümüzde hala matematikçileri şaşırtmaya devam ediyor. Yaşamlarımızdaki kaosta ve tesadüflerde kimi durumlarda matematiksel bir düzen var gibi gözüküyor. Ayrıca göz atmak isterseniz: Dünyanın En Basit Teoremi, Dünyada 8.000 Kişinin Kafasında Aynı Sayıda Saç Teli Olduğunu Gösteriyor
Kaynaklar ve ileri okumalar:
- How a simple observation from the 1800s about patterns in big data sets can fight fraud; Yayınlanma tarihi: 10 Kasım 2015; Kaynak site: Conversation. Bağlantı: How a simple observation from the 1800s about patterns in big data sets can fight fraud;/
- Looking out for number one; Yayınlanma tarihi: 1 Eylül 1999; Bağlantı: https://plus.maths.org/content/looking-out-number-one
- Cerasa A. Testing for Benford’s Law in very small samples: Simulation study and a new test proposal. PLoS One. 2022 Jul 22;17(7):e0271969. doi: 10.1371/journal.pone.0271969. PMID: 35867697; PMCID: PMC9307211.
- What Is Benford’s Law? Why This Unexpected Pattern of Numbers Is Everywhere. Yayınlanma tarihi: 8 Mayıs 2023. Kaynak site: Scientific American. Bağlantı: What Is Benford’s Law? Why This Unexpected Pattern of Numbers Is Everywhere
Matematiksel











Makaleleri severek okuyorum, emeğinize sağlık.
sizi canı gönülden kutluyorum. Çığır açmışsınız ardı gelir inşallah kardeşim