
Matematikte ilginç isimli teoremler sıklıkla karşımıza çıkar. Bunlardan bir tanesi de Pizza teoremidir. Pizza teoremi hakkında bilgi vermeden önce süreci aklınızda canlandırmaya çalışalım.
Diyelim ki, arkadaşınız ile birlikteyken evde yemek olmadığını fark ettiniz ve bir pizza sipariş ettiniz. Ancak arkadaşınızın pizzayı geleneksel dilimleme biçiminin dışına çıkarak, ortasından geçmeyen iki dikey kesim ile dilimledi. Sonra da dilimlerden büyük olanı yemek istedi. Size de bu durumda küçük dilimlerden birisi kalacak gibi gözüküyor.
Öfkeyle bıçağı elinize aldınız ve mevcut iki dilimin kesişim noktasından geçen iki kesik daha attınız. Şimdi aşağıdaki şekilde de görebileceğiniz gibi hepsi de 45 derecelik açıya sahip 8 diliminiz var. Bu son durumun ardından arkadaşınıza bir öneride bulunuyorsunuz.
Büyük dilimi önce siz alırsınız. Sonrasında ikiniz de saat yönünde ilerleyerek bir sonraki dilimi yemeye devam edersiniz. Ya da tam tersi büyük dilimi önce arkadaşınız alır ve süreç aynı biçimde devam eder. Sizce bu durumda pizzadan kim daha çok yiyecektir?
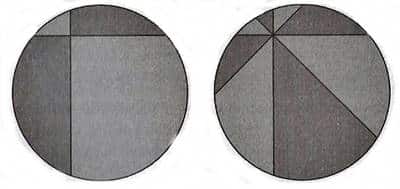
Pizza Teoremi
Bu problem ilk kez 1968’de “Mathematics Magazine” dergisinde yer aldı. Yayınlanan çözüm analitik olarak çeşitli alanları hesaplarken bir gerçeği açığa çıkardı. Her iki durumda da aslında bir fark yoktu. Yemeğe kim önce başlarsa başlasın sonuçta herkes eşit miktarda pizza yemiş oluyordu.
İnsanların büyük çoğunluğu için hikâye burada biter. Ortada bir sorun vardır ve çözülmüştür. Ama matematikçiler için durum farklı elbette. 1994’te Larry Carter ve Stan Wagon yine “Mathematics Magazine” sayfalarında yeni bir eşitlik gösterdiler.
Hatta aksine pizzanın uyumlu kısımlardan oluştuğu için tamamen aynı toplam alana sahip dört dilimlik iki grubun yer aldığı ek bir alt bölünmenin farklı bir çizimini göstererek bunu kanıtladılar.
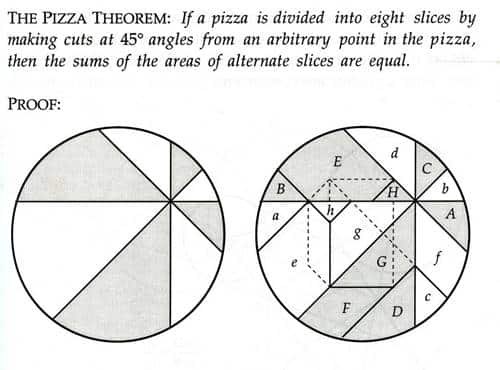
Şimdi sıra genellemede. Pizzanın içinde herhangi bir nokta alalım, pizzayı aynı açı ile 2n dilime bölen noktadan geçen 2n kesim yapalım ve dilimleri en başta açıklandığı gibi iki gruba ayıralım. Eğer pizza 4n parçaya bölünürse kişi sayısı n olduğu sürece eşit miktarda bir bölünme sağlanabilir. Bu durumda eğer üç kişi varsa pizza on iki dilime bölünür ve herkes memnun olacağı eşit miktarda dilime sahip olur.
Ayrıca pizza yani aslında bir daire rastgele bir noktadan eşit açılarla kesilerek 8, 12, 16… bölümlere ayrılırsa birer atlayarak hesapladığınız zaman dilimlerin alanlarının toplamı eşit olacaktır. Bu nedenle siz ve arkadaşınız birer birer pizza dilimlerini yediğiniz sürece bu koşulları sağlayan bir pizzadan her daim eşit miktarda yemiş olabilirsiniz.
Teoremin farklı kanıtlarını incelemek içinde bu siteyi kullanabilirsiniz. Ancak pizza hakkında daha anlatacaklarımız bitmedi.
Matematik Bilen Biri Paradan Tasarruf İçin Hangi Boy Pizzayı Tercih Etmelidir?
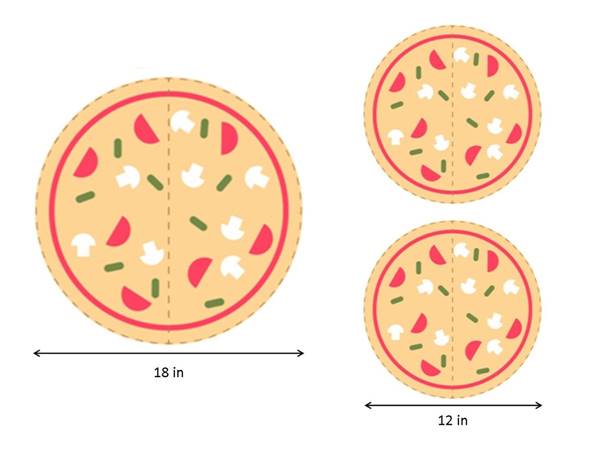
Madem pizza ile başladık, yine pizza ile devam edelim. Diyelim ki bu sefer karnınız acıktı ve eve pizza siparişi vermeye karar verdiniz. Bu esnada büyük bir ihtimalle aklınıza şu soru gelmiş olabilir. Büyük boy mu yesem yoksa orta boy mu? İki orta boy pizzamı yersem daha çok doyarım yoksa bir büyük boy mu?
Her ne kadar sezgileriniz size iki orta boy pizzanın daha çok olduğunu söylese de siz yine de sezgilerinize değil matematiğe güvenin. Daha küçük boy bir pizza sipariş etmek daha ucuz olsa da, muhtemelen en uygun maliyetli seçenek değildir. Sipariş verirken büyük boy pizza isteyin. Neden derseniz kısaca açıklayalım.
Bildiğiniz gibi pizzalar daire biçimindedir. Diyelim ki pizzalardan bir tanesinin çapı 18 cm diğerinin de 36 cm olsun. Bu durumda birinin yarıçapı 9, diğerinin ise 18 cm olacaktır. Bize alan hesabı gerekiyor. Karmaşık hesaplamalardan arınmak için hadi pi sayısını da 3 olarak alalım.
Bu durumda orta boy pizzanın alanı 3.92 = 243 cm2 olur. Ancak büyük boy pizzanın alnı 3. 182=972 cm2 olacaktır. 972/243=4 sonucunu elde edersiniz. Yani aslında alan büyük boyda 4 katına çıkmıştır. işte bu nedenle de büyük boy pizza yemek daha avantajlıdır.
Ancak siz yine de sipariş vermeden önce boyutunu isteyip hesap yapmayı unutmayınız. Ayrıca pizza hakkında okumaya devam etmek isterseniz: Gauss İle Bir Dilim Pizzanın İlgisi Nedir? Cevap Gauss Eğrileri
Kaynaklar ve ileri okumalar:
- Math and Pizza Unite: The Pizza Theorem; Bağlantı: https://www.mathcon.org
- Pizza math: For the best price, you should always order the biggest pie; yayınlanma tarihi: 20 Ocak 2022; Bağlantı: https://bigthink.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










