
Ondalık sistem, on parmağımızın olması gibi basit bir nedenden dolayı yaygın olarak tercih edilen sayma sistemimizdir. Ancak bilindiği gibi günümüzde kullandığımız onluk sayma sistemi sadece bir kabuldür. Tarihe göz attığımızda, Maya medeniyetinin 20’lik, Babil medeniyetinin de 60 lık sayı sistemi kullandığını biliyoruz. Bilgisayar dünyasına giriş yaptığımızda 2, 8 ve 16 sık olarak kullanılan başka sayı sistemleri ile karşılaşıyoruz.
Ayrıca Mısırlıların aslında on parmaklarıyla değil, parmakları arasındaki on iki eklem ile sayıları saydığını da biliyoruz. Bu noktada da kimilerinin aklına şu soru geliyor. Acaba kullandığımız onluk sayı sistemi bizim matematik becerilerimizi sınırlandırıyor mu? Günümüzde bir çok kişi bu sorunun cevabını evet olarak vermekte. Bu kişiler bizlere bir alternatif olarak on ikili sayı sistemini öneriyorlar.
On İkili Sayı Sistemi Yani Düzine Sistemi Nedir?
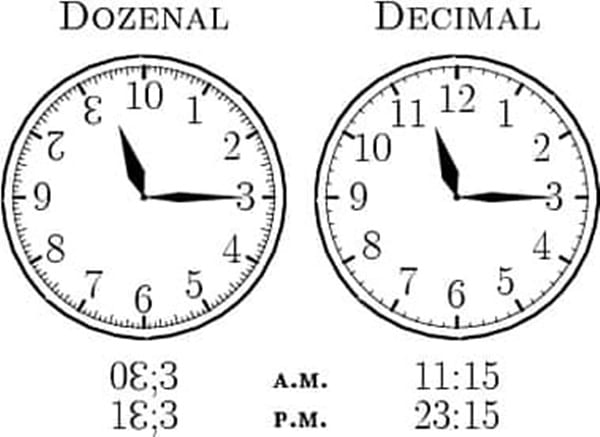
On ikili sayı sisteminde on iki rakam vardır. 0’dan 9’a kadar olan sayılar ve on bir( X) ve on iki için(E) ekstra yeni rakamlar yani toplamda 0,1,2,3,4,5,6,7,8,9,X,E,10. (Görselde gördüğünüz gibi, X bir baş aşağı 2 ve E bir baş aşağı olarak 3 olarak yazılıyor. Biz font yetersizliğinden yazamadık.)
Sistemdeki 10 sayısı 12 olur ve “doh” biçiminde okunmaktadır. . Sonraki on iki sayı bu şekilde ‘doh’ ön ekiyle listelenecektir. Yani doh-1 (11), doh-2 (12), doh-3 (13) gibi. 20 sayısı 2-doh olarak adlandırılır ve sonraki sayılar 2-doh ön ekiyle listelenir. Örneğin 21 sayısı 2-doh-1 olarak okunur. 12’lik sayma sisteminin, onluk sisteme göre daha iyi olarak kabul edilmesinin sebebi de bölen sayısının daha fazla olması nedeniyle uygulama kolaylığıdır.
12 sayısı 2, 3, 4 ve 6’ya bölünebilirken 10 sadece 2 ve 5 ile bölünmekte. Gündelik yaşamımızda 5 yerine 3 ya da 4 ile bölmeyi daha çok tercih ederiz. Eğer 12 elmanız varsa ikişer olarak 6 torbaya, üçerli olarak 4 torbaya, dörderli olarak 3 torbaya ve altışarlı olarak iki torbaya ayırabilirsiniz.
Oysa on elmayı ikişerli olarak 5 ve beşerli olarak 2 torbaya bölebilirsiniz. Elbette, sistem ilk bakışta şaşırtıcı görünüyor. Ancak ondalık sistem ya da alfabe, onunla ilk kez karşılaşan bir çocuk için de öyledir. Ancak sisteme alıştıktan sonra, faydalarının zahmete değer olduğunu anlamaya başlarız.
12’lik Sayı Sistemi Savunucuları
Bunun ilk savunuculardan birisi Duodecimal Arithmetick adlı kitabıyla fikri ortaya atan Joshua Jordaine’dir. 12’likler ile saymak kadar doğal ve eşsiz bir şey olmadığını ileri sürmektedir. On sekizinci yüzyılda, on ikilik sayı sistemin iyi tanınan takipçilerinin arasında, icat ettiği ve dünyaya yayılan stenografı sistemiyle büyük bir üne kavuşan Isaac Pitman bulunmaktadır.. Ayrıca Viktorya dönemi sosyal teorisyenlerinden olan Herbert Spencer da bu sistemi destekler.
Bu sistemi yakın zaman taşıyan ise F. Emerson Andrews tarafından yazılan ve The Atlantic Monthly’nin Ekim 1934 sayısında yayınlanan Duodecimal Society of America, ya da DSA’nın oluşumuna yol açan bir makaledir. Devamında kardeş bir topluluk olan Dozenal Society of Great Britain 1959 yılında kuruldu. Hala iki topluluk da, onluk sistemle olan savaşlarını sürdürmekteler. Bu sistemin savunucularının temel argümanı, 12 lik sayı sistemin özellikle çocuklar ve öğrenciler için matematiği kavramlaştırmayı ve anlamayı kolaylaştırmasıdır.
Haklı olabilirler mi?
Bölünebilirlik çarpım tablolarıyla da ilişkilidir. Herhangi bir tabanda öğrenilmesi en kolay olan sayılar tabanı bölen sayılardır. Bu yüzden onluk tabanda, 2 ve 5’in çarpım tablosunu ezberlemek kolaydır. Çünkü basit bir örüntü içerir. Aynı biçimde 12’lik sistemde en basit çarpım tabloları 2, 3, 4 ve 6’ya bölünenlerdir.
Eğer her bir satırın son iki basamağına bakarsanız, 2, 3, 4 ve 6’nın bir şablonla ilerlediğini görürsünüz. Bu nedenle birçok kişi için sıkıntı olan çarpım tablosunu ezberlemek daha kolaydır. 12’lik sayı sisteminin çarpım tablosunu öğrenmede kolaylık sağlaması bir yana, en büyük avantajı kesirleri ortadan kaldırması.
Onluk tabanda bölme yapmak istediğinizde genellikle sorun çıkartır. Örneğin 10 ‘un üçte biri 3,33 … ,’tür ve üçler sonsuza kadar devam eder. Dörde bölümü 2,5 tir ve yine ondalık bir anlayış gerektirir. Oysa ki 12 tabanında 10’un üçte biri 4’tür dörtte biri ise 3’tür. Yüzdelik olarak ifade edersek üçte biri yüzde kırk, dörtte biri yüzde otuzdur. Karmaşık kesirlerden kurtulmak işlerin daha kolay yürümesini sağlayabilir gerçekten…
Dünyanın 12’lik sayma sistemine geçmesi mümkün mü?

Hepimizin bildiği gibi bu değişim hem karmaşık hem de çok pahalı olacaktır. Saatlerimiz, ölçü birimlerimiz, paramız her şeyin değişmesinden bahsediyoruz. Ayrıca günümüz teknolojisi ile artık bir çoğumuz zihnimizden işlem yapmak yerine daha pratik cihazlar kullanıyoruz. Ancak, sistemin savunucularına göre bu mümkün.
Onlara göre işe önce paradan başlamalı, sonra da eğitim sisteminde yapılacak değişiklikler ile desteklenmelidir. Söylediklerine göre devamında, bir zaman içinde her şey yerli yerine oturacak ve kimse eski sayı sistemini kullanmak istemeyecektir. Ne dersiniz, düzineler ile düşünmenin zamanı gelmiş olabilir mi? Ayrıca benzer bir konuya daha göz atmak isterseniz: Bir Gün Neden 24 Saat, Bir Saat Neden 60 Dakika?
Kaynaklar ve İleri Okumalar
- Dozenalists of the world unite! Rise up against the tyranny of ten!; yayınlanma tarihi: 12 Aralık 20ı2; Bağlantı: https://www.theguardian.com/
- Why We Should Switch To A Base-12 Counting System; https://io9.gizmodo.com/
- The Curious Case For Base 12 (Why Dozens Are Easier For Everyday Maths Than Tens); https://steemit.com/
Matematiksel

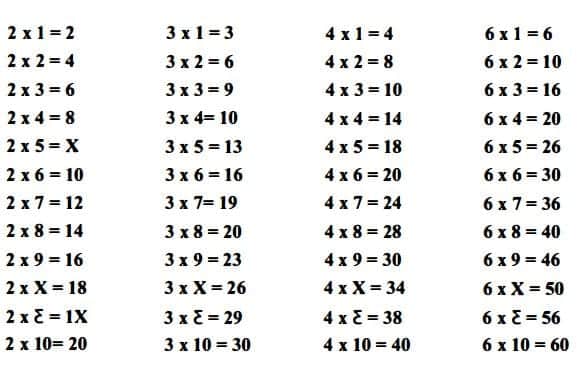










Dünyayı iyilik güzellik
ve matematik kurtaracak.