Matematik ve bilgisayar bilimi, genellikle sıradan insanların aklını zorlayan teoriler ve formüllerle doludur. Ancak bazı formüller, yalnızca karmaşık olmaktan öteye geçip hayal gücümüzü zorlayan sonuçlar da doğurabilir. Tupper’ın Kendini Çizen Formülü, buna bir örnektir.
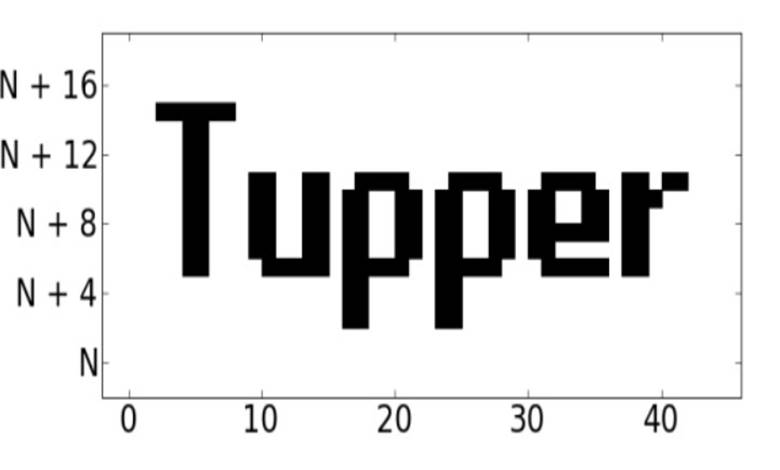
Tupper Formülü, ilk kez Kanadalı matematikçi Jeff Tupper tarafından 2001 yılında tanıtılmıştır. Bu formül, belirli bir matematiksel sistemi kullanarak bir görselin oluşturulmasını sağlar. Bu formüle baktığınızda kaotik ve karmaşık bir matematiksel yapı görünebilir. Ancak asıl ilginç olan, formülün görselleştirilmesi sonucunda ortaya çıkan şeydir: formül kendi grafiğini çizer!
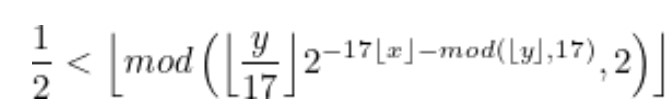
Bu formülde:
- x ve y: Görselin piksel koordinatlarını temsil eder.
- n: Formülün çıktısını değiştiren sabit bir büyük sayıdır.
- mod: Modüler aritmetik işlemi, yani bir sayının bir başka sayıya bölümünden kalanını verir.
- Üst kısmı olmayan parantez ise, matematikte taban fonksiyonu temsil eder. Yani içine yazılmış olan sayıyı aşağı yuvarlar.
Tupper Formülü Nasıl Çalışıyor?
Tupper Formülü, aslında bir bit haritası olarak çalışan bir sistemdir. Yani, ikili sayılar üzerinden pikselleri temsil eder. Formül, (x, y) koordinat düzlemindeki noktaların değerlerine göre bir doğruluk veya yanlışlık durumu üretir ve bu sonuç, piksellerin siyah mı yoksa beyaz mı olacağını belirler. Eğer (x,y) koordinatındaki pikseller “doğru” bir sonuç üretirse siyah (dolgu) olur. Aksi takdirde beyaz (boş) kalır.
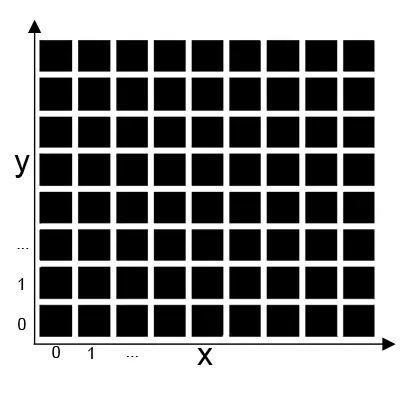
Formülün anahtarı olan n, istenen şeklin matematiksel bir temsilidir ve (110101001…) gibi uzun bir ikili sayı dizisidir. Bu ikili dizideki her bir bit, bir pikselin siyah mı yoksa beyaz mı olduğunu belirler. Formül, n’nin bitlerini 17 birim yüksekliğinde bir matris içinde çözümler.
Y ekseni, 17 birimlik bölümlere ayrılır ve her bölüm n’nin bir parçasına karşılık gelir. X ekseni boyunca ilerleyerek de her sütunda piksel renkleri belirlenir. Sonuç, bir doğruluk testi (0.5<mod) ile piksellerin siyah mı beyaz mı olacağını belirler.
N sayısını Değiştirerek İstediğiniz Her Şeyi Çizmeniz Mümkündür
Evet, Tupper Formülü teorik olarak her şeyi çizebilir! Çünkü her olası şekil, yeterince uzun bir n sayısı ile temsil edilebilir. Sonucunda, her görsel, belirli bir bit haritası kombinasyonudur. Tüm kombinasyonlar, bir sayı ile ifade edilebilir. Doğru n sayısını kullanarak bu kombinasyonu formülde oluşturabilirsiniz.
Örneğin, bir kalp şekli için, şeklin öncelikle ikili bit dizisini hesaplayın. Sonrasında, bu diziye karşılık gelen n’yi bulun. Devamında da formülü çalıştırarak görseli oluşturun. Bunu denemeniz için hazırlanmış bazı araçlar da mevcuttur. Tupper’s Self-Referential Formula Playground bunlardan birisi.
Sonuç Olarak
Herhangi bir görselin, matematiksel bir sayıya indirgenebileceği fikri, hem estetik hem de felsefi bir perspektif sunar. Formül, bize şunu hatırlatıyor: Matematik, yalnızca bir bilim değil, aynı zamanda her şeyin temelinde yatan bir sanat!
Kaynaklar ve ileri okumalar:
- The formula that plots (almost) everything. Yayınlanma tarihi: 3 Ağustos 2017; Kaynak site: Plus math. Bağlantı: The formula that plots (almost) everything
- The ‘Everything’ Formula – Numberphile. Yayınlanma tarihi: 15 Nisan 2015; Bağlantı: https://www.youtube.com/
- Tupper, Jeff. (2001). Reliable two-dimensional graphing methods for mathematical formulae with two free variables. Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 2001. 77-86. 10.1145/383259.383267.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





