Bir çok kişiye matematik soğuk, soyut bir konu gibi görünür. Oysa ki bu tutkulu ve hayat dolu Evariste Galois bize başka bir matematikçi modeli sunar.

Herhangi bir alanda önemli bir katkı hakkında konuştuğumuzda, bunu her zaman “devrimci” olarak tanımlarız. Belki de bu terimi o kadar çok kullanıyoruz ki, sonunda anlamından bir kısmını yitirir. Ancak Évariste Galois iki alanda gerçek devrimciydi.
20 yaşında trajik bir şekilde öldü, ancak bu siyaset veya matematik yüzünden değil, romantik bir deha efsanesini oluşturan bir sebepten dolayı olacaktı.
Evariste Galois Ne Yaptı?
İkinci dereceden denklemlerin çözümü için genel formül, dokuzuncu yüzyıl civarında biliniyordu. Üçüncü ve dördüncü dereceden denklemlerin çözümü için kullanılan formüller ise on altıncı yüzyılın ilk yarısında keşfedildi. Doğal olarak sıradaki hedef, beşinci dereceden denklemlerdi.
Galois’ dan önce, 300 yıl boyunca birçok matematikçi umutsuz bir biçimde çözümü verecek formülleri bulmaya çalıştı ama bir işe yaramadı. Peki 5 sayısını özel şey yapan şey nedir? Bu soru Evariste Galois’i de rahatsız ediyordu. Sonunda Galois teorisi ile soyut cebirin iki alt alanını birbirine bağlayacaktı. Bu iki alan grup teorisi ve cisimler idi.

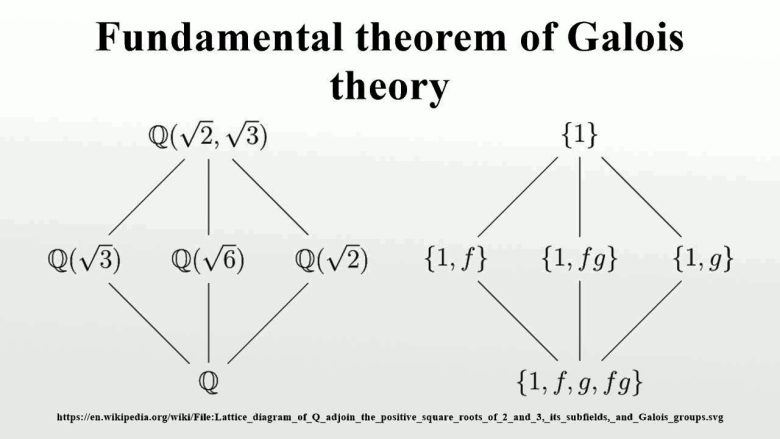
Özetle 2. ve 3. dereceden genişlemeler sonucu permütasyon gruplarında bir takım özel değişimlerin olduğunu fakat derecesi 4 ve üzerinde olan denklemlerin oluşturduğu genişlemelerle bağlantılı olan permütasyon gruplarında düzenli bir şekilde değil anlamsız bir şekilde ortaya çıktığını ve genel bir çözüm ortaya konamayacağını ispatladı. Aramanın da boş anlamsız bir çaba olduğunu ortaya koydu.
Galois teoremlerinin önemli bir kısmının lisans düzeyinde bir matematikçinin karşısına asla çıkmayacağını belirtmeliyim. Mazisi bin yılı aşan bir probleme verdiği anti-cevap hiç şüphesiz büyük bir işti. Bu işi yapan ise nihayetinde 21 yaşında bir genç adamdı. Bu sarsıcı çalışmasını bir gece sabaha kadar çalışarak yazmıştı. Peki yine de aşk bunun neresinde? Sanırız hikayeyi baştan anlatmalıyız.
Kısaca Evariste Galois Kimdir?
Evariste 1811 yılında Büyük Fransız İhtilali’nin, Napolyon’a yenik düşüp boyun eğdiği yıllarda dünyaya geldi. Ailesi varlıklı ve nüfuzluydu. Siyaset ailesinden geliyordu. Babası Nicolas-Gabriel Galois, Paris yakınlarındaki Bourg-la-Reine kasabasının belediye başkanıydı.
Klasik eğitimden gelen annesi Adelaide-Marie Demante, erken çocukluğunda Évariste’i evde eğitmeye başladı. Çocuk on iki yaşında okula gitmeye başladığında, devrimci doğası, büyük siyasi gerginliklerle çalkalanan bir Fransa’da yüzeye çıkmaya başladı.
Henüz 14 yaşındayken Legendre’nin Elements de Geometrie eserini bir roman okur gibi okuyup kısa sürede bu alanda uzmanlaştığı söylenir. Ve aynı yıl kendi başına pek çok büyük matematiksel çalışmayı okur ve bitirir.
Ardından Fransa’nın en yetkin eğitim kurumu Ecole Polytechnique’in sınavına hiçbir hazırlık yapmaksızın girer. Fakat hâlâ anlaşılamayan bir şekilde sınavda başarılı olamaz. Vazgeçmez, cebirsel yapılar hakkında iki önemli makalesini dönemin büyük matematikçilerinden Cauchy’ye gönderir. Beklentisi Cauchy’nin kendisine referans olarak Polytechniqe’e girmesine yardımcı olmasıdır.
Fakat bu olmaz. Zira Cauchy ona çalışmalarını kaybettiğini onları bulmasının mümkün olmadığını söyleyecektir. Sonucunda referansı olmadığı için tekrar sınava girer. Ancak sınavdan birkaç gün önce babası cumhuriyetçiliğinin bedelini ödeyecektir. Kendisine yönelik ithamları gururuna yediremez ve oğlunun çalışma odasının üst katında oğlu çalışmaya devam ederken kendisini asar.
Bu Evariste için hiç kapanmayacak ağır bir yara olur. Seviyesine göre oldukça düşük bir okul olan Ecole de Normal’e başlar. Burada cebir üzerine ciddi çalışmalar yapma fırsatı bulur ve bu çalışmalarını derleyerek bir yarışma için Fransız Bilimler Akademisi sekreteri, matematikçi Fourier’e yollar.
Eğer gerçekten Galois’nın hayatını anlamak istiyorsak onun hayatının temel özetinin şanssızlık olduğunu anlamalıyız. Zira Fourier onun çalışmasını okuyamadan hayatını kaybeder. Ve o kargaşada Galois’nın çalışması ortadan kaybolur ve değerlendirilmeye alınmaz. Vazgeçmez, aynı yıl cebir ve sayı kuramı üzerinde üç önemli makalesini yayımlar. Ve bu çalışmalarda grup, normal alt grup kavramlarını oluşturur. Henüz 19 yaşındadır.
Evariste Galois romantik bir devrimci idi
Devrim sokaklarda alevlenirken, Galois ve okulun diğer öğrencileri duvarların ardında kilit altında tutuluyordu ve basına yazdığı bir mektupta bununla ilgili şikayette bulunması, okuldan atılmasına yol açtı. Okuldan atıldıktan sonra, Ulusal Muhafızların Topçu Birliği’ne katılarak devrim için çalışmaya başladı ancak kısa süre sonra tutuklanacaktı.
Talihsizlik onun kaderiydi. Ve o bu kadere meydan okuyordu. Belki bu kaderi seviyordu ve bu kaderi elleriyle yaratıyordu. Hapisten kısa süre sonra çıktı. 14 Temmuz 1831’de Bastille protestolarına kapatılan birliğinin üniforması ve tüfeğiyle katıldı. Bu kez yasadışı üniforma giymek suçundan tutuklandı ve 6 ay hapis yattı.
6 ayın sonunda hapisten hasta ve yorgun bir halde çıktı. Kaderindeki son halkada aşk vardı. Hapisten sonra tedavi gördüğü merkezdeki hekimin kızı Stephanie aşık olacağı kızdı. İnanılmaz güzellikte bir kızdı ve kahretsin ki nişanlıydı. Galois bunu umursamadı, kıza aşkını ilân etti…

Onun ölümünün yüzyıllar sonrasında muhtemelen onun hakkında hiçbir şey bilmeyen bir Türk şairin, Turgut Uyar’ın dizeleri ona sesleniyor gibidir. Yüzyıllar sonra yaşayan Türk şair haklıdır. Kızın nişanlısı öfkelenir ve Galois’yı düelloya davet eder.
üç kere üç dokuz eder bilirsin
Turgut Uyar -Sibernetik
birin karesi birdir karekökü de bilirsin
mutlu aşk yoktur bilirsin..
Evariste Galois’in Son Gecesi
Evariste Galois gerçekten şanssızdır, nitekim hasmı onun dahil olduğu birlikteki subaylardan biridir ve gerçekten iyi bir nişancıdır. Galois’nın elleri ise bir matematikçinin elleridir. Galois kazanması mümkün olmayan bu düello davetini reddedemeyecek kadar da cesurdu. Düello davetini kabul eder. 21 yaşındadır ve şimdi acelesi vardır. 29 Mayıs gecesi yani düellodan bir gece önce tüm çalışmalarını birleştirip derli toplu bir hale getirmeye çalıştı.

Çalışmasının kenarına şu notları yazdı. “Vakit yok”, “güneş neredeyse doğacak”, “keşke biraz daha zamanım olsaydı” Notlarının sonunda dostu Chavalier’e şu notu yazdı: “Jacobi ya da Gauss’a açıkça bu teoremler hakkında doğru olup olmaları konusunda değil, önemleri hakkında fikirlerini sor. Daha sonra, umarım, bu karmaşayı çözmenin kendi yararlarına olacağını anlayacak bazı kişiler olacaktır.” Mektubu tamamlayıp Chavalier’e teslim etmesi için kardeşi Alfred’e verdi.
30 Mayıs 1833 sabahının erken saatlerinde düelloda yere düşen Evariste Galois olur. Doktora zamanında yetiştirilemez. 21 yaşındaki genç adam matematikte bir devrim yaptığı gecenin sabahında ölür. Kardeşi mektubu Chavalier’e ulaştırır.
Galois’nın ölümünden 10 yıl sonra Akademi Galois’nın çalışmasını onaylar. Ve genç adam makus talihine karşı verdiği amansız savaşta yüreğindeki tüm aşkı; bilme aşkını, sevme aşkını, devrim aşkını birbiriyle çarpar ve sonsuzluğa, kendi sonsuzluğuna ulaşır. Yüzyıllar sonra yaşayan Türk şair yine haklı çıkacaktır.
“…
Turgut Uyar -Sibernetik
ama baharda ya da dışarda
sonsuz göğün altında
aşkın aşkla çarpımı,
her zaman sonsuzluktur.
ve karekökü de yoktur.
Kaynaklar ve ileri okumalar için:
- Évariste Galois, the Teenager Who Revolutionized Mathematics. Yayınlanma tarihi: 31 Mayıs 2016. Kaynak site: BBVA Mind. Bağlantı: Évariste Galois, the Teenager Who Revolutionized Mathematics
- Genius, stupidity and genius again; Yayınlanma tarihi: 1 Mayıs 2005. Kaynak site: Plus Math. Bağlantı: Genius, stupidity and genius again
Matematiksel





