Milenyum Soruları, 2000 yılında Clay Matematik Enstitüsü tarafından belirlenen ve çözülmeleriyle matematiğin sınırlarını genişleteceğine inanılan yedi temel matematik problemidir

Her birine titiz bir çözüm sunabilenlere 1 milyon dolarlık ödül vaat edilmektedir. Ancak bu soruların zorluğu, onları yalnızca azimli matematikçilerin üzerine düşünebileceği karmaşık birer entelektüel meydan okuma yapmaktadır.
Rus matematikçi Grigori Perelman, bu sorulardan biri olan Poincaré Varsayımı için bir çözüm sunmuş, ancak ödülü reddetmiştir. Diğer altı soru hâlâ çözülmeyi beklemektedir.

Milenyum Soruları Nelerdir?
- 1- Yang-mills ve Kütle Aralığı: Çözülmedi
- 2- Riemann Hipotezi: Çözülmedi
- 3- P NP’ye karşı Problemi: Çözülmedi
- 4- Navier–Stokes Denklemleri: Çözülmedi
- 5- Hodge Kestirimi: Çözülmedi
- 6- Poincare Kestirimi: Çözüldü
- 7- Birch ve Swinnerton-Dyer Kestirimi: Çözülmedi
Riemann Hipotezi

Matematik tarihinde çözülmesi en zor ve en önemli problemlerden biri olan Riemann Hipotezi, 1859 yılında Bernhard Riemann tarafından ortaya atılmıştır. Asal sayıların sayı doğrusu üzerindeki dağılımıyla ilgilenen bu hipotez, matematiğin hem temel yapı taşlarını hem de modern uygulamalarını derinden etkiler.
Riemann Hipotezi, “Riemann zeta fonksiyonu” adı verilen karmaşık bir matematiksel yapıya dayanır. Bu fonksiyon, asal sayıların dağılımını anlamada kilit bir rol oynar. Hipotezin özü, Riemann zeta fonksiyonunun sıfır yapan değerlerinin belirli bir düzlemde nasıl düzenlendiğiyle ilgilidir.
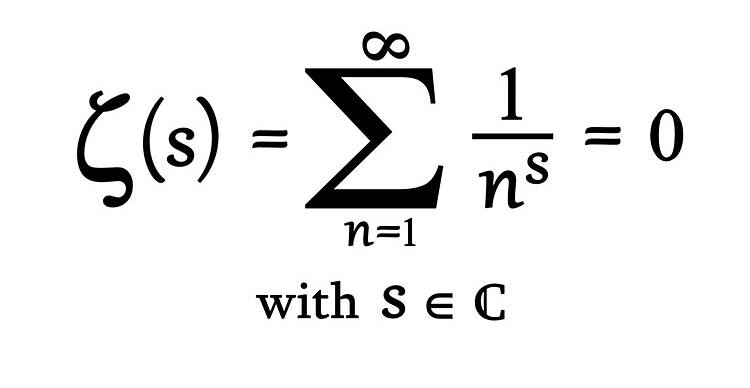
Riemann zeta fonksiyonu, karmaşık sayılar düzleminde tanımlıdır ve belirli bir sayıya kadar kaç asal bulunduğunu tahmin etmek için kullanılır. Hipotez, zeta fonksiyonunun x = 0 ile x = 1 arasındaki kritik bölgede sonsuz sayıda sıfır yapan değerinin tümünün x = 1/2 doğrusu üzerinde olduğunu öne sürer.
Riemann Hipotezi’nin çözümü için ortaya atılan sayısız varsayım ve yöntem bulunmakla birlikte, bu yöntemlerin hepsi büyük matematiksel zorluklar barındırır. Hipotezin basitçe bir “evet” veya “hayır” cevabı gerektirmesine rağmen, bu cevaba ulaşmak için kullanılan araçlar son derece karmaşıktır.
Bu milenyum problemi, asal sayılar dışında görünüşte ilgisiz alanlarda ortaya çok sık olarak çıkar. Bu nedenle, kanıtlamanın (veya çürütmenin) önemi, sayı teorisinin veya bir bütün olarak matematiğin sınırlarının çok ötesine geçer. Riemann hipotezi kanıtlanabilirse kuantum dünyasında bir çok hesaplanamayan fenomen için bize bazı yöntemler gösterecektir.
Yang – Mills Hipotezi

Kuantum fiziğinin temel prensiplerinden biri olan dalga-parçacık ikiliği, parçacıkların bazen bir dalga gibi, bazen ise bir nokta parçacık gibi davranabileceğini ifade eder. Bu özellik, kuantum dünyasının temel taşlarından biridir. Ayrıca, modern teknolojilerin—elektronik cihazlar, nano malzemeler ve kuantum bilgisayarlar gibi—temelini oluşturur.
Yang-Mills teorisi, bu davranışı ve temel parçacıkların etkileşimlerini açıklamak için geliştirilmiş matematiksel bir çerçevedir. Teori, parçacıkların boşlukta tanımlanan pozitif bir kütle boşluğuna sahip olduğunu ve bu nedenle sıfır kütleli olmalarının mümkün olmadığını öne sürer. Bu, nükleer kuvvetlerin doğasının anlaşılmasında kritik bir adımdır.
Yang-Mills teorisi, doğadaki temel kuvvetlerin açıklanmasında kritik bir rol oynar. Özellikle, bu parçacıkların neden sıfır kütleli olmadığını açıklar. Ayrıca, protonlar ve nötronlar gibi çekirdek parçacıkları bir arada tutan güçlü nükleer kuvvetlerin doğasını matematiksel olarak anlamak için temel bir yapı sunar. Ancak ispatlanması, karmaşık matematiksel teknikler gerektirir.
P – NP Problemi

Eğer matematikçiler bilgisayar biliminin “P’ye karşı NP” sorusunu doğru şekilde çözebilirse, çözümün karşılığında elde edeceklere ödül 1 milyon dolardan çok daha fazlası olacaktır.
P Sınıfı; Bilgisayarların polinom zamanda çözülebileceğik problemleri ifade eder. Bu, bir algoritmanın, belirli bir girdi boyutuna bağlı olarak, makul bir süre içinde çözüm bulması anlamına gelir. Buna bir örnek sayıların çarpımı olacaktır. NP Sınıfı ise bilgisayarların bir çözümü hızlı bir şekilde (polinom zamanda) doğrulayabildiği problemleri ifade eder.
P = NP ifadesi, P sınıfındaki problemlerin, NP sınıfındaki problemlere eşit olup olmadığını sorar. Eğer P = NP ise, zor gibi görünen tüm NP problemleri, aslında kolayca çözülür hale gelir. Ancak, eğer P ≠ NP ise; NP sınıfındaki birçok problem için hızlı bir çözüm üretmek mümkün olmayacaktır.
P ve NP probleminin çözümü, yalnızca matematiksel bilgi gerektirmekle kalmaz. Aynı zamanda derin bir teorik kavrayış ve yaratıcı yaklaşım gerektirmektedir. Bu sorunun cevabı, yalnızca matematiği değil, teknoloji, ekonomi ve toplumun işleyişini de kökten değiştirecektir.
Navier-Stokes Denklemleri

Navier-Stokes denklemleri, sıvıların ve gazların hareketini modellemek için kullanılan matematiğin temel araçlarından biridir. Bu denklemler, akışkanların davranışını ve hareketini anlamak için geliştirilmiş kısmi diferansiyel denklemler kümesidir.
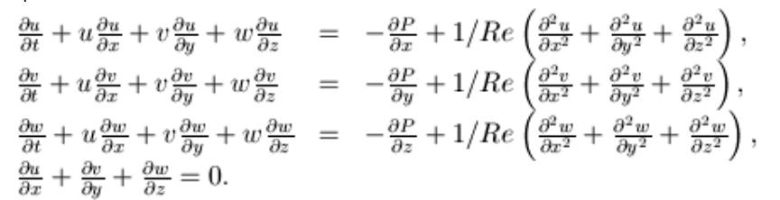
Milenyum sorusu, Navier-Stokes denklemleri ile ilgili şu iki temel soruyu sorar:
- Çözümlerin Varoluşu: Denklemler her durumda geçerli bir çözüm sunar mı?
- Sınırlılık: Bu çözümler her zaman sonlu kalır mı? Yoksa belirli koşullarda sonsuz büyüklükler (örneğin, türbülans) mi üretir?
Navier-Stokes denklemlerinin çözümleri, fiziksel dünyayı daha derinlemesine anlamamızı sağlayacaktır. Bu, yalnızca matematikte değil, aynı zamanda teknoloji, mühendislik ve çevre bilimlerinde de devrim yaratacaktır.
Hodge Varsayımı

Hodge Varsayımı, Milenyum Problemleri arasında en soyut ve en karmaşık olanlardan biridir. Problem, cebirsel geometri ve topolojinin kesişim noktasında yer alır ve karmaşık matematiksel şekillerin basit yapı taşlarından oluşturulup oluşturulamayacağını sorgular. Matematikçiler, bu soruyu yanıtlamak için soyut matematiksel yapıları ve simetrileri anlamaya çalışıyor.
En basit haliyle, bir şeklin, daha temel matematiksel yapı taşlarından inşa edilip edilemeyeceğini inceler. Bu, karmaşık şekillerin daha anlaşılır parçalara ayrılıp ayrılamayacağını anlamaya çalışmak gibidir. Bu yapı taşlarına Hodge çemberleri denir, ancak bunların cebirsel çemberlerden türetilip türetilemeyeceği hala bir muammadır.
Hodge varsayımı, matematiğin soyut güzelliğinin bir simgesidir. Problem, yalnızca karmaşık şekillerin anlamını değil, aynı zamanda matematiğin bir bütün olarak doğasını da sorgular. Çözümü, matematik dünyasına hem derin bir anlayış hem de ilham verecek bir dönüm noktası olacaktır
Birch ve Swinnerton-Dyer Varsayımı

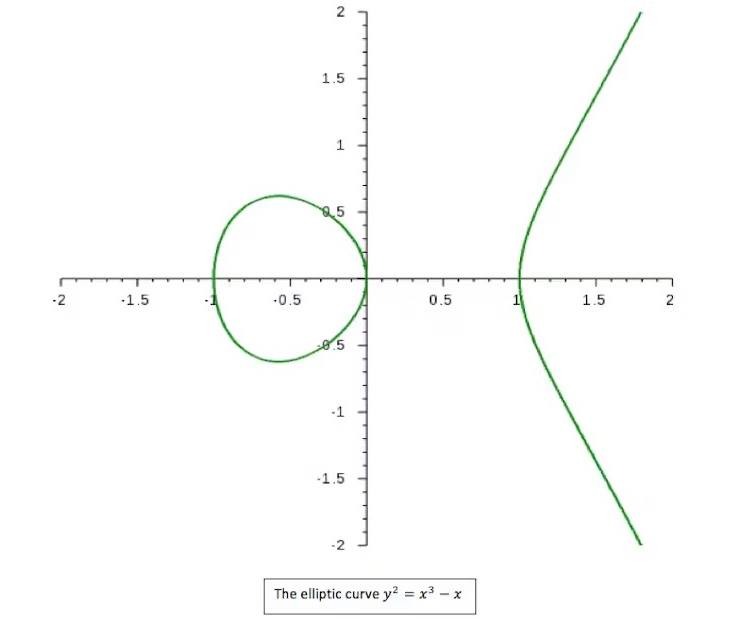
Eliptik eğriler y 2 = x 3 + a x + b biçiminde ifade edilmektedir. Bir eliptik eğri üzerinde kaç tane rasyonel çözüm (kesirli sayılarla ifade edilebilen noktalar) vardır? Bu soru, Birch ve Swinnerton-Dyer Varsayımı olarak isimlendirilir.
Bu eğri üzerindeki çözümler, x ve y’nin rasyonel sayılar olduğu noktalardır. Varsayım şunu söyler. L-fonksiyonu adı verilen bir matematiksel yapı, bu eğri üzerindeki rasyonel çözümler hakkında bilgi verir. Eğer L-fonksiyonu sıfırsa, sonsuz sayıda rasyonel çözüm vardır. Eğer L-fonksiyonu sıfır değilse, sınırlı sayıda rasyonel çözüm vardır.
Varsayım, asal sayılar ve rasyonel sayılarla ilgili daha derin anlayış sağlar. Fermat’nın Son Teoremi gibi önemli problemlerin çözümünde kullanılan yöntemlerle ilişkilidir. Ayrıca, kriptografide kullanılan eliptik eğri şifreleme sistemleri bu tür matematiksel yapıların anlaşılmasına dayanır.
Kaynaklar ve ileri okumalar:
- An eminent mathematician claims to have solved one of math’s greatest mysteries. And it’s one of 6 problems with a $1 million prize. Yayınlanma tarihi: 25 Temmuz 2018. Kaynak site: Business Insider. Bağlantı: An eminent mathematician claims to have solved one of math’s greatest mysteries. And it’s one of 6 problems with a $1 million prize.
- How Numbers Work; Discover the strange and beautiful world of mathematics; New Scientist Books
Matematiksel