Sevin ya da nefret edin, Rubik Küpü ya da ülkemizde kullanılan adıyla zeka küpü, dünyanın en popüler bulmacalarından biridir. İlk olarak 1974 yılında, Macar heykeltıraş ve mimar Ernö Rubik tarafından “Sihirli Küp” adıyla geliştirilen bu oyuncak, 80’li ve 90’lı yılların başında dünya genelinde milyonların ilgisini çekmeyi başarmıştır.

Bir Rubik Küpünü çözmekte zorlanıyorsanız üzülmeyin, çünkü yalnız değilsiniz. Aslında Ernö Rubik‘in bile kendi icadını çözmeyi öğrenmesi bir ayını almıştı. Bunun nedenini anlamak oldukça basittir. Sonuçta, standart bir 3×3 Rubik Küpü, 43 kentilyondan fazla olası kombinasyona sahiptir. Ancak bu devasa sayı içindeki kombinasyonlardan yalnızca tek bir doğru çözüm bulunur.
Bu nedenle, bir Rubik Küpünü yalnızca kaba kuvvetle, yani deneme-yanılma yöntemiyle çözmeye çalışmak çok uzun zaman alır. Süreci hızlandırmak ve etkili bir şekilde çözmek için bazı stratejiler öğrenmeniz gerekir. Bu stratejileri öğrendikten sonra, Rubik Küpünü çözmek çok daha kolay ve keyifli hale gelecektir.

Rubik Küpü En Hızlı Çözme Rekoru Kime Aittir?
Rubik Küpü’nü en hızlı çözme rekoru, sürekli olarak gelişen bir alandır ve “Speedcubing” adı verilen bu spor dalı, dünya genelinde binlerce kişiyi bir araya getirir. Şu anda 3×3 Rubik Küpü çözme dünya rekoru, Yusheng Du adlı Çinli bir oyuncuya aittir. Yusheng Du, bu rekoru 3.47 saniyede çözerek 2018 yılında kırmıştır.
Bu başarı, modern çözüm teknikleri, hızlı eller ve Rubik Küpü algoritmalarını ezberleme becerisinin bir kombinasyonudur. Yusheng Du’nun kullandığı algoritma, Dr. Jessica Fridrich tarafından geliştirilmiştir. Bu yöntem, özellikle “Speedcubing” turnuvalarında başarıya ulaşmak isteyenler için en etkili çözüm tekniklerinden biri olarak kabul edilir.

Rubik Küpü’nü Tanıyalım
Rubik Küpü’nü çözmeye başlamadan önce, onu tanımak önemlidir. Bir Rubik Küpü, her biri büyük küpün üçte biri boyutunda olan 27 küçük küpten oluşur. Bu küçük küpler, küpün altı farklı renkten oluşan yüzeylerini oluşturur.
Rubik Küpü’nün her yüzünde bir merkez parça bulunur ve bu merkezler, küpü bir arada tutan çekirdek iskeleye bağlıdır. Merkez parçalar sabittir ve her yüzün ana rengini belirler. Küpü ambalajından çıkardığınızda, her yüz aynı renkte düzenlenmiştir. Göreviniz ise küpü olası milyonlarca kombinasyondan birine karıştırmak ve ardından orijinal düzenine geri döndürmektir.

Rubik Küpü’nün hareketli parçaları iki ana gruba ayrılır: köşe küpleri ve kenar küpleri. Bu parçaların işlevlerini ve yerlerini anlamak, küpü çözmek için önemli bir adımdır.
Rubik Küpü’nde 12 adet kenar küpü bulunmaktadır. Bu küpler, her bir kenarda yer alır ve iki farklı renkten oluşur. Kenar küplerini doğru hizalamak, Rubik Küpü’nün tamamlanması için gereklidir. Rubik Küpü’nün merkezinde yer alan sabit küpler, her yüzün ana rengini belirler ve tek yüzlüdür. Standart bir küpte beyaz sarının karşısında, kırmızı turuncunun karşısında ve mavi yeşilin karşısındadır.
Rubik Küpü Matematik Açısından Neden Önemlidir?

Rubik Küpü, matematiğin soyut dünyasından somut sonuçlar çıkartmayı mümkün kılan eğlenceli bir bulmacadır. Onu bu kadar ilginç ve karmaşık kılan şey, üç boyutta da döndürülebilmesidir. Bu özelliği sayesinde, standart bir 3x3x3 Rubik Küpü, tam olarak 43.252.003.274.489.856.000 farklı kombinasyona sahiptir. Bu sayı (3 8 x 8!)(2 12 x 12!)/12 biçimindedir.
Rubik Küpü’nde toplamda 8 köşe küpü vardır. Bu küpler, 8! farklı şekilde düzenlenir. Ayrıca her köşe küpü, birbirinden bağımsız olarak 3 farklı yönde döner. Bu da köşe küpleri için toplam 3⁸ x 8! yol olduğunu gösterir. Bu da bize birinci parantezimizi açıklar.
Küpte toplamda 12 kenar küpü vardır ve bunlar 12! farklı şekilde düzenlenir. Ayrıca her kenar küpü, 2 farklı yönde döner. Bu nedenle kenar küpleri için toplam 2¹² x 12! yol vardır. Bu da ikinci parantezimizi açıklar.
Bu iki değeri çarptığımızda şu sonucu elde ederiz: (3⁸ x 8!) (2¹² x 12!) = 519.024.039.293.878.272.000 Ancak bu kombinasyonların çoğu, Rubik Küpü’nün fiziksel olarak mümkün olan hareketleriyle elde edilemez. Matematikçiler, yalnızca 12’de biri kadar kombinasyonun geçerli olduğunu belirlemiştir. Bu da bize 43.252.003.274.489.856.000 sayısını verir.
3×3’lük Bir Rubik Küp Nasıl Çözülür?
Bir Rubik Küpü’nü çözmek için belirli bir yöntem veya algoritmayı takip etmek gerekir. Farklı çözüm teknikleri olsa da, burada temel ve öğretici bir yaklaşımı ele alıyoruz. Bu yöntem, özellikle yeni başlayanlar için etkili bir rehberdir.
1- Yüz ve Renk Seçimi
Çözüm sürecine başlamak için bir yüz ve bir renk seçmelisiniz. Seçtiğiniz renk, o yüzün merkez karesinde bulunan renk olmalıdır. Unutmayın, merkez küpler sabittir ve her yüzün ana rengini temsil eder. Çalışmalarınız boyunca bu yüzü üst yüz olarak kabul edin ve işlemlere buradan başlayın.
2- Beyaz Artıyı Oluşturma
Seçimimizi beyaz renkten yana yapalım. İlk hedefiniz, beyaz bir artı oluşturmaktır. Bunun için küp üzerindeki beyaz içeren kenar küplerine odaklanmanız gerekir. Bu kenar küplerinin, yan yüzlerdeki merkez parçalarla uyumlu olması şarttır. Örneğin: beyaz/mavi kenar parçası, beyaz merkezle mavi merkezin arasında hizalanmalıdır.
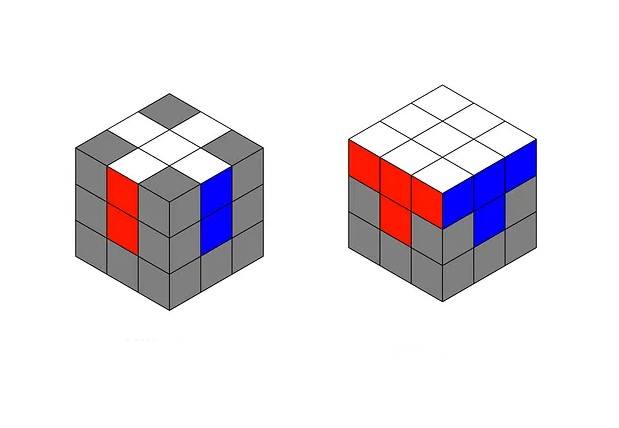
Bu şekilde, toplamda dört kenar parçasını doğru bir şekilde yerleştirerek beyaz artıyı tamamlamalısınız. Aynı zamanda her kenar parçasının ikinci rengi, ilgili yan yüzdeki merkezle de eşleşmelidir.
Beyaz artıyı oluşturduktan sonra, sıradaki adım köşe küplerini doğru bir şekilde yerleştirmektir. Köşe küplerini yerleştirirken, her köşedeki renklerin, yan yüzlerdeki merkez parçalarla hizalanarak küpün üst katmanında bir renk bandı oluşturması gerekir.
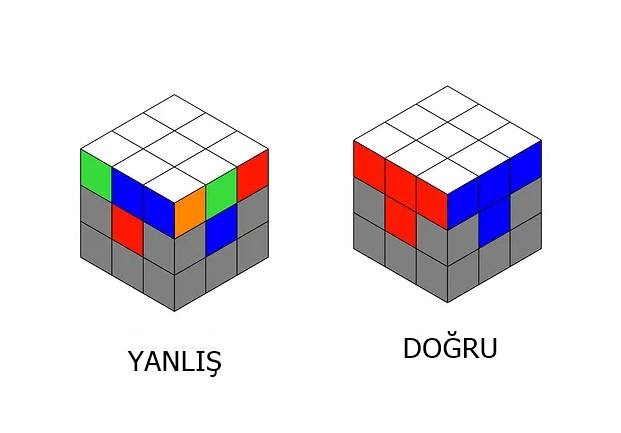
Bu adımda birçok kişi hata yapar ve köşe küpleri yanlış yerlere yerleştirir. Bu durum, küpün geri kalanını çözmeyi imkânsız hale getirir. Köşe küpleri doğru pozisyona oturtmadan ilerlemek mümkün olmadığından, bu adım oldukça kritik bir öneme sahiptir.
Rubik Küpü: Orta Katman Çözümü
Rubik Küpü’nün bir sonraki adımı, küpü ters çevirerek beyaz yüzü alt tarafa yerleştirmekle başlar. Bundan sonra, orta katmanı çözmek için çalışmanız gerekir. Bu adım, küpün kalan sekiz kenar parçasından dördünü doğru konumlarına yerleştirerek orta katmanı tamamlamayı hedefler. Bu işlem, Rubik Küpü’nün üçte ikisini tamamlamış olmanızı sağlar.

Küpü inceleyerek, orta katman kenar küplerinde beyaz olmayan renkleri bulun. Bu kenar küpler, yerleştirilmek üzere doğru yüzlere taşınacaktır. Örneğin, kırmızı/mavi kenar küpü, kırmızı ve mavi merkez karelerin bulunduğu yüze yerleştirilmelidir.
Kenar küpünü doğru pozisyona taşımak için, kenar küpünü uygun merkeze hizalayın. Örneğin, kırmızı/mavi kenar küpü, kırmızı merkezin altına hizalanmalı ve mavi yüze bakmalıdır. Daha sonra, aşağıdaki iki algoritmadan birini kullanabilirsiniz. Bu algoritmalar, kenar küplerini orta katmanda doğru pozisyona taşır.
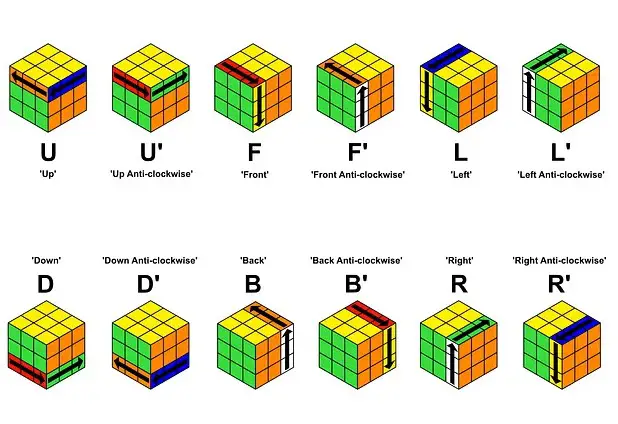
- Sağa Taşıma Algoritması:
Eğer kenar küpü sağdaki yüzeyde olması gerekiyorsa:
U R U’ R’ U’ F’ U F - Sola Taşıma Algoritması:
Eğer kenar küpü soldaki yüzeyde olması gerekiyorsa:
U’ L’ U L U F U’ F’
Sarı Artı ve Sarı Yüzün Çözümü
Rubik Küpü’nün üçüncü adımı, sarı yüzü çözmektir. Bu aşamada, küpün sarı yüzünde bir artı oluşturup ardından köşe küplerini doğru pozisyonlarına döndürerek sarı yüzü tamamlamayı hedefliyoruz. Sarı yüzü çözmeye başlamak için ilk hedefiniz sarı artıyı oluşturmaktır. Sarı yüzün başlangıçta üç farklı durumu olabilir:
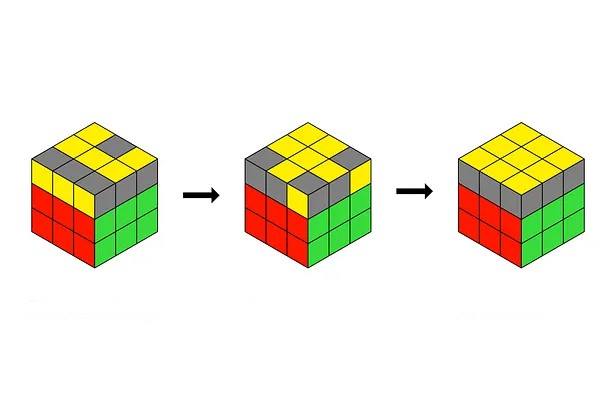
- Bir L şekli oluşmuş (Bir köşe ve ona bitişik kenar sarı).
- Hiç sarı kenar parçası yok (Sadece ortada sarı merkez vardır).
- Bir çizgi oluşmuş (Yatay veya dikey).
Küpü elinize alın ve sarı merkezi yukarı bakacak şekilde yerleştirin. Sonrasında da F R U R’ U’ F’ algoritmasını uygulayın. Bu algoritmayı bir veya iki kez tekrarladığınızda sarı yüzde bir artı şekli oluşacaktır.
Sarı artıyı oluşturduktan sonra, artıyı oluşturan sarı kenar küplerin yan renklerini kontrol edin. Bu renkler, yan yüzlerdeki merkez renklerle eşleşmelidir. Yan renkler doğru değilse, küpü uygun şekilde döndürerek bu eşleşmeyi sağlamanız gerekir.
Sarı artıyı tamamladıktan sonra, sıradaki adım sarı köşe küplerini doğru pozisyona yerleştirmektir. Sarı köşe küplerin doğru yerlerde olup olmadığını kontrol edin (diğer renkleri ilgili yan yüzlerle uyumlu olmalı). Eğer köşe küpler yanlış yerlerdeyse, U R U’ L’ U R’ U’ L algoritmasını uygulayın.
Bu adımların sonunda sarı yüz tamamen çözülmüş olacaktır. Bu işlem sırasında sabırlı olun ve her adımı dikkatlice takip edin. Sarı yüzü tamamladığınızda, küpün son aşamasına geçebilirsiniz: kenar parçalarını hizalayarak çözümü tamamlamak.
Rubik Küpü ve “Tanrı’nın Sayısı”

Matematikçiler, 3×3’lük standart bir Rubik Küpü için her karıştırılmış durumda en fazla 20 hamlede çözümün mümkün olduğunu kanıtlamıştır. Bu, küpün karıştırılma şekli ne kadar karmaşık olursa olsun, doğru algoritmalar kullanıldığında en fazla 20 hamle ile çözülebileceği anlamına gelir.
Bu minimum hamle sayısına ulaşmak için kullanılan algoritmalara Tanrı’nın algoritması denir. 20 sayısı ise Tanrı’nın sayısı olarak adlandırılır. İnsanlar tarafından kullanılan bilinen tüm çözüm yöntemleri, genellikle bu optimal değerden çok daha fazla hamle gerektirir.
Yani bir Rubik Küpü, ne kadar karmaşık görünürse görünsün, çözüm her zaman en fazla 20 hamle uzaklıktadır. Ancak burada dikkat çeken bir sorun var: 43.252.003.274.489.856.000 farklı kombinasyondan kaç tanesinin bu maksimum 20 hamleye ihtiyaç duyduğunu hala tam olarak bilmiyoruz. Bu yüzden, eğer küpü çözmek için daha fazla hamle harcıyorsanız, endişelenmenize gerek yok—bu tamamen normal!
Kaynaklar ve ileri okumalar için:
- The Amazing Math Inside the Rubik’s Cube; Yayınlanma tarihi: 4 Ekim 2022; Kaynak site: Popular Mechanics. Bağlantı: The Amazing Math Inside the Rubik’s Cube
- How hard is the Rubik’s cube? Yayınlanma tarihi: 4 Temmuz 2011; Kaynak site: Plus Maths. Bağlantı: How hard is the Rubik’s cube?
Matematiksel