Dünyanın birçok yerinde matematikçiler yıllardır üç kulübe problemi, elektrik-su-doğal gaz problemi ya da üç ev üç kuyu problemi adıyla bilinen bu basit görünümlü matematik sorusunun cevabını arıyor.
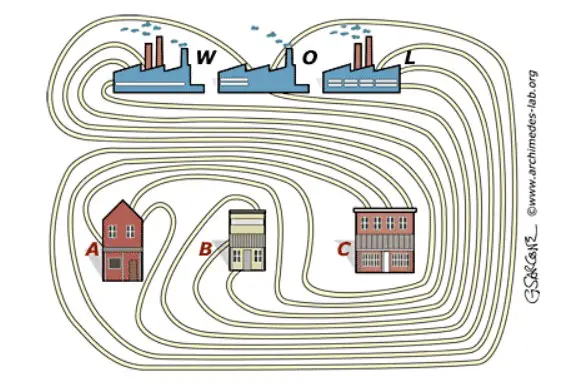
Bu sorunun ilk kez kimin tarafından ortaya atıldığına dair kesin bir bilgi yok. Ünlü bulmaca yazarı Sam Loyd, problemi 1903 yılında yayımlamıştı. Ancak bu bulmacanın ondan çok daha önce var olduğuna ve Loyd’un yalnızca farklı bir versiyonunu paylaştığına inanılıyor. Günümüzde de problemin çeşitli versiyonları internette dolaşıyor. Eğer henüz karşılaşmadıysanız kısaca açıklayalım.
Üç Ev Üç Kuyu Problemi Nedir?
Aslında problem oldukça basit görünüyor. Üç eviniz ve üç kuyunuz var. Her evden her kuyuya birer boru döşemek istiyorsunuz. Ancak şart şu: borular birbirinin üzerinden ya da altından geçmemeli. Yani her evi her hizmete bir çizgiyle bağlarken, bu çizgilerin kesişmemesi gerekir.
Problemin diğer bir versiyonu ise şöyle: üç ev var ve her birine elektrik, su ve doğalgaz bağlamak gerekiyor. Burada da aynı kural geçerli. Tüm bağlantıları yaparken hatların birbirini kesmemesi mümkün mü? Konuyu daha iyi anlamak için verilen çizime göz atabilirsiniz.
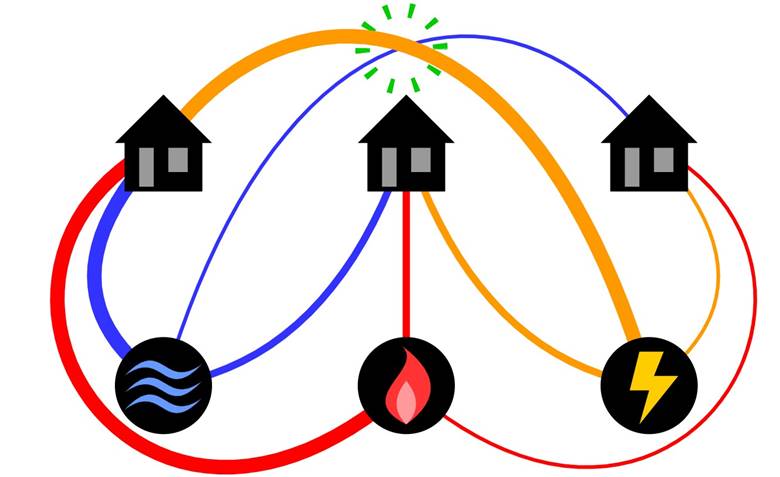
Görselde de görebileceğiniz gibi, üç ev problemi bu çizimde çözülememiştir. Aslında işin gerçeğini baştan söyleyelim ki yıllarınızı harcamayın: Bu sorunun bir kağıt üzerinde, yani iki boyutta çözümü imkansızdır. Ne yaparsanız yapın, borulardan en sonuncusu daha önce çizdiğiniz bir bağlantıyla mutlaka kesişir.
Bu problemin çözümü ancak torus (bir tür halka şeklindeki yüzey) ya da Möbius şeridi gibi farklı topolojik yüzeylerde mümkündür.
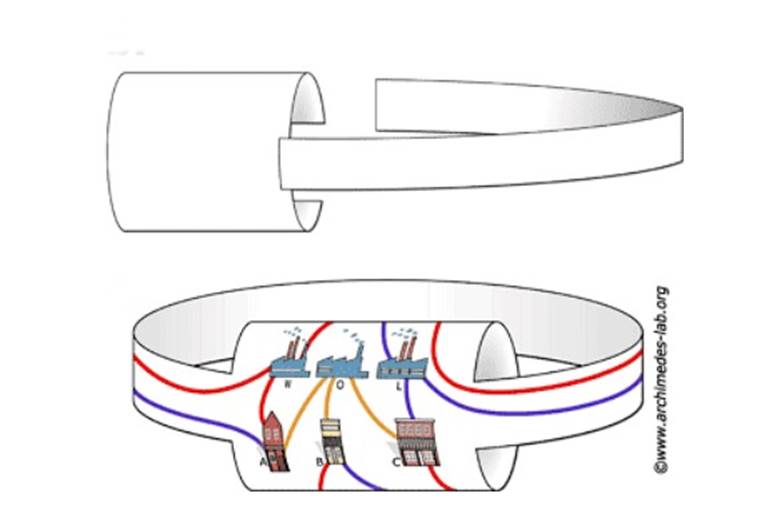
Örneğin, aşağıdaki şekilde bunun nasıl çözülebileceğine dair bir örnek görebilirsiniz. Önce bulmacayı düz bir kağıda çizin. Sonra kağıdı bir silindir haline getirin. Ardından şekilde gösterildiği gibi bir kağıt şerit daha ekleyin. Böylece üç ev ile üç kuyu arasında gerekli tüm bağlantıları kesişmeden kurabilirsiniz.
Üç Ev Üç Kuyu Problemini Çözmek Neden İmkansızdır?
Bu problemin matematikteki karşılığı 3’e 3 tam iki parçalı graf olarak bilinir. İki parçalı (bipartite) ifadesi, grafın noktalarının iki ayrı kümeye ayrılabildiğini ve tüm bağlantıların bu iki farklı kümedeki noktalar arasında kurulduğunu anlatır. Üç hizmet probleminde bu kümelerden biri evleri, diğeri ise su, elektrik ve doğalgaz gibi hizmetleri temsil eder.
Tam (complete) ifadesi ise her evin tüm hizmetlerle bağlantılı olduğunu gösterir. Yani farklı kümelerdeki her nokta çifti bir hat ile birbirine bağlanır.
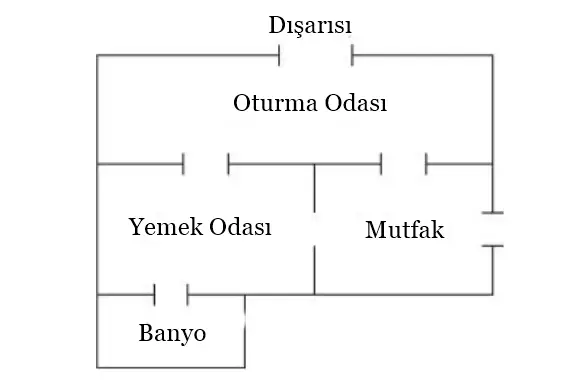
Bir grafikte, kenarlar köşeleri birbirine bağlar. Bu yüzden kat planını incelerken hangi nesnelerin birbirini bağladığını düşünmemiz gerekir. Şimdi odaları köşeler olarak ele alalım. Odaları birbirine bağlayan kapıları ise bu köşeleri birleştiren kenarlar şeklinde çizelim.
Örneğin, oturma odası, mutfak ve yemek odasının her birinde üç kapı bulunur. Dışarıya yalnızca oturma odası ve mutfaktan çıkış vardır. Banyo ise sadece yemek odasına bağlıdır. Bu kurallara göre oluşturduğumuz grafik aşağıdaki gibi görünecektir.
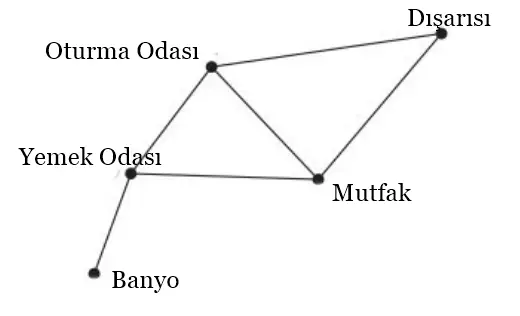
Gördüğünüz gibi bu matematiksel yapıda kenarlar ( E: edge) ve köşeler ( V: vertex) önemlidir. Ancak kenar, köşe ve Euler adı geçtiği anda bilmeniz gereken bir başka matematiksel kuram daha vardır. Buna Euler karakteristiği denir. Aynı zamanda Euler’in Çokyüzlü Formülü olarak da bilinmektedir.
Euler’in formülü bize örneğin, tam olarak yedi kenarı olan bir basit çokyüzlünün var olamayacağını söyler. Bunu anlamak için karton, makas ve yapıştırıcıyla model yapmaya gerek yoktur. Aynı şekilde, on yüzü ve on yedi köşesi olan bir basit çokyüzlünün de olamayacağını bu formülü kullanarak gösterebiliriz.
Euler’in formülü bize şu temel ilişkiyi verir: V – E + F = 2. Yani, köşe sayısı eksi kenar sayısı artı yüz sayısı her zaman ikiye eşittir. Bu formüldeki 2 sayısı, iki boyutlu bir düzlemi temsil eder.
Burada V, grafikteki köşe yani nokta sayısını gösterir. E, kenar sayısını ifade eder; her kenar iki köşeyi birbirine bağlar. F ise grafikteki yüz sayısıdır. Yüz, kenarlarla çevrelenmiş kapalı bir bölgeyi tanımlar.
Gördüğünüz gibi, bu yaklaşım matematikçilere genelleme yapma ve karmaşık soruları daha kolay çözme imkânı sunar. Aynı mantık, bizim problemimizi analiz ederken de işimize yarar ve çözüm bulmamıza yardımcı olur.
Tüm Bunların Üç Kulübe Problemi İle İlgisi Nedir?
Şimdi kulübeleri ve kuyuları köşe (V) olarak kabul edelim. Bu iki kümede toplamda 6 nokta bulunuyor, yani V = 6. Bunları birleştirecek borular ise kenar (E) olacak ve bunların sayısı 9, yani E = 9.
Euler’in formülünü hatırlayalım: V – E + F = 2. Sayıları yerine koyalım: 6 – 9 + F = 2. Bu denklemi çözersek:
F = 2 + 9 – 6; F = 5 olur. Sonuç olarak, bu bağlantıların iki boyutlu bir düzlemde kesişmeden çizilebilmesi için gerekli yüz sayısının (F) 5 olması gerekir.
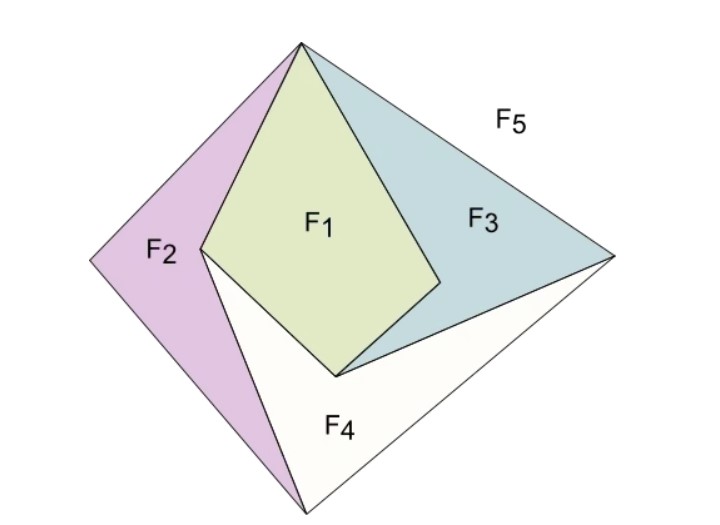
Bu beş yüzü yukarıdaki görselde çizmeye çalıştığınızda, her yüzün mutlaka 4 kenar ile sınırlanması gerektiğini görürsünüz. Ayrıca her kenar iki köşe arasında yer almalıdır.
Elimizde 5 yüz varsa, toplamda 4 × 5 = 20 kenar olması gerekir. Her kenarın iki köşeyi bağladığını düşünürsek, bu kadar kenarı yerleştirebilmek için en az 10 köşe gerekir. Oysa başta elimizde yalnızca 9 köşe olduğunu biliyoruz. Bu çelişki gösteriyor ki, üç kulübe probleminin iki boyutlu bir düzlemde kesişmesiz şekilde çözülmesi mümkün değildir.
Kaynaklar ve ileri okumalar
- The Three Utilities Problem. yayınlanma tarihi: 19 Nisan 2019; bağlantı: The Three Utilities Problem
- The Water-Gas-and-Electricity Puzzle. Bağlantı: The Water-Gas-and-Electricity Puzzle
Matematiksel