Kalıplar, düşünme sürecinizi basitleştirmeye yarayan zihinsel kısayollardır. Ancak kimi zamanlarda bu kısa yollar sonucunda hatalı kararlar da alırız. Buna bir örnek bağlaç yanılgısı (conjunction fallacy) denilen durumdur.

Konu hakkında daha fazla bir bilgi vermeden bir soru soralım. Diyelim ki arkadaşınız Aysel ile bir konsere gitmeye karar verdiniz. Ancak Aysel konsere gelirken yanında daha önce hiç tanışmadığınız iki arkadaşını daha getireceğini söyledi. Bu kişilerden birisinin matematikçi, diğerinin ise müzisyen olduğunu da söyledi.
Konser zamanı gelip Aysel’in arkadaşları Begüm ve Ahmet ile tanıştığınız zaman, Begüm’ün gözlük taktığını ve biraz utangaç olduğunu, Ahmet’in ise daha dışa dönük olduğunu, ayrıca salaş bir tişört ve kot pantolon ile konsere geldiğini gördüğünüzü düşünelim.

Geçinmek için ne iş yaptıklarını sormadan, Begüm’ün bir matematikçi ve Ahmet’in ise müzisyen olması gerektiğini varsayabilirsiniz. Ancak belki de yanılıyorsunuzdur. Çünkü Ahmet matematikçidir ve Begüm ise müzik ile uğraşıyordur.
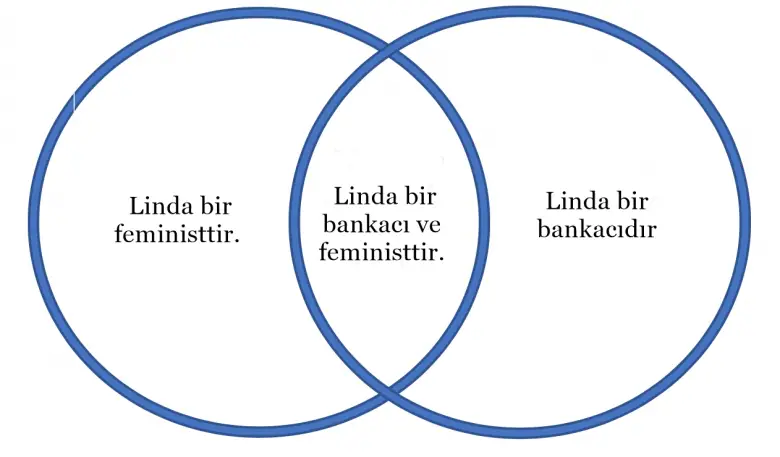
Bağlaç yanılgısı, insanların iki olayın birlikte meydana gelme olasılığının, her iki olayın tek başına meydana gelme olasılığından daha yüksek olduğuna inanma eğiliminde olduğu bir olgudur. Bağlaç yanılgısının klasik örneği de aslında yukarıda aktardığımız benzer bir hikayenin etrafında şekillenmektedir. Hikayemizin kahramanı Linda adında bir kız olduğu için de aynı zamanda Linda problemi adı ile bilinmektedir.
Bu problem bilişsel yanılgılarla ilgili yazılarda karşımıza sıklıkla çıkan ve davranışsal iktisadın en etkili isimlerinden ikisi olan Daniel Kahneman ve Amos Tversky tarafından ortaya atılmıştı. Her şey 1970’lerde, ikilinin etkili bir dizi deney rehberliğinde hepimize, zeki insanların aslında irrasyonelliğe yatkın olduğunu göstermesiyle başladı. Geniş yelpazedeki senaryolar çevresinde yapılan deneyler gösterdi ki; insanlar mantık yerine sezgilerine dayalı kararlar verme eğilimindeydi.
Linda Problemi Nedir?
“Linda 31 yaşında, bekar, açık sözlü ve çok zeki bir genç kadın. Lisede felsefe ile ilgilenmeye başlamıştı. Devamında üniversiteye gitti. Bir üniversite öğrencisi olarak, ayrımcılık ve sosyal adalet meselelerine ilgi duyuyordu. Her zaman vatandaşların eşitlik haklarını savunurdu. Ayrıca nükleer karşıtı gösterilere de katılırdı.”
Şimdi bu bilgi göz önüne alındığında, iki ifadeden hangisinin daha fazla doğru olma ihtimali var mı? (A) Linda bir banka memurudur. (B) Linda bir banka memurudur ve feminist hareket içinde aktif biçimde rol almaktadır. Çoğu insan gibi düşünüyorsanız, B diyeceksinizdir. Zaten araştırmaya katılanların yüzde seksen beşi de B’yi seçmişti. Ancak ne yazık ki bu yanlış cevap. Cümleler birbirinden bağımsız iki olayı tanımlıyor. İkinci cümlede ve kelimesi ise her şeyi değiştirir.
Sorunun tam olarak ne olduğunu anlamak için biraz olasılık konusunu hatırlayalım. İki bağımsız olayın meydana gelme olasılığı, meydana gelen her olayın olasılıkları çarpılarak bulunur. Bu çarpma sonucunda elde edeceğimiz olasılık da her zaman bağımsız olayların olasılıklarından daha küçük olacaktır. Diğer bir deyişle iki olayın eşzamanlı olarak meydana gelme olasılığı, her iki olayın da tek başına meydana gelme olasılığından her zaman daha az veya ona eşittir.
Linda Problemi İle İlgili Sorun Nedir? Neden Bağlaç Yanılgısına Düşüyoruz?
Linda problemini şu şekilde düşündüğümüz zaman yaptığımız hatayı anlamamız daha kolay olur. Şu cümlelerden hangisi daha olasıdır: (1) yarın sabah lastiğiniz patlayacak veya (2) yarın lastiğiniz patlayacak ve siyah arabalı bir adam yardım etmek için duracak. Bu durumda, (2)’nin en olası sonuç olmadığı açık olmalıdır. Muhtemel bu nedenle de 1 nolu cevabı tercih etmiş olmalısınız.

Linda’nın banka memuru olma olasılığının yüzde 0,9 olduğunu düşünelim. Linda’nın feminist harekette aktif olma olasılığı da yüzde 0,05 olsun. Dolayısıyla, Linda’nın bir banka memuru olma ve feminist harekette aktif olma olasılığı 0,9 ile 0,05 çarpımı kadardır. Sonuç yüzde 0,045’tir. Bu yüzde 0,05’ten azdır. Bu durumda mantık çerçevesinde seçilmesi gereken doğru cevap aslında A’dır. Yanlışlık, Linda’nın yaşam şekliyle bir feministin yaşam tarzını temsil ettiği ve tipik banka memurunu temsil etmediği için ortaya çıkmaktadır.
Bağlaç yanılgısı hayatın birçok alanında günlük olarak ortaya çıkar. Yanlışlık, modern toplumda o kadar yaygındır ki, her gün sayısız insan bu düşünceye kapılır. Linda problemi en iyi bilinen örnek olsa da, araştırmacılar bağlaç yanılgısını güvenilir bir şekilde ortaya çıkaran düzinelerce problem geliştirdiler.
Neden olasılıkları hep ihmal ediyoruz?
Olasılık kavramlarının öğrenilememe nedenlerinden biri de bu yazıda ele aldığımız türdeki kavram yanılgılarıdır. Benzer şeyleri bir arada gruplandırmak, dünyayı anlamlandırma şeklimizin önemli bir parçasıdır. Aslında kategorize etmeyi tamamen olumsuz bir şey değildir.

İnsanlarla, nesnelerle veya hayvanlarla her etkileşim kurduğumuzda, ne yapacağımızı bilebilmek için kategorileri hakkında öğrendiğimiz bilgileri kullanırız. Alışılmadık şeyler veya insanlar hakkında karar vermeye çalışırken, tüm kategoriyi temsil eden bir örnek olarak bu ortalamaya -prototipe- başvururuz. Prototipler, yukarıdaki örneklerde de olduğu gibi, olasılık hakkındaki tahminlerimize rehberlik eder.
Ancak kategorilere olan güvenimiz, farkında olmasak bile kolayca önyargıya dönüşebilir. Bu önyargılardan kaçınmak zordur. Bununla birlikte, bunun farkında olmak iyi bir başlangıçtır. Araştırmalar, insanların bu tip yanılgılarının farkına vardıklarında, genellikle yargılarını düzelttiklerini göstermiştir. Bu nedenle de konu hakkında bilgilenmemiz ve de bilgilendirmemiz önemlidir.
Kaynaklar ve ileri okumalar:
- Why do we use similarity to gauge statistical probability? Bağlantı: https://thedecisionlab.com/biases/representativeness-heuristic
- Can you outsmart this logical fallacy? – Alex Gendler; yayınlanma tarihi: 25 Kasım 2019; Bağlantı: https://www.youtube.com/
- ‘Linda the Bank Teller’ Case Revisited; yayınlanma tarihi: 22 Kasım 2016; Bağlantı: https://www.psychologytoday.com/
- Wojciechowski BW, Pothos EM. Is There a Conjunction Fallacy in Legal Probabilistic Decision Making? Front Psychol. 2018 Apr 5;9:391. doi: 10.3389/fpsyg.2018.00391. Erratum in: Front Psychol. 2018 Nov 27;9:2281. PMID: 29674983; PMCID: PMC5895783.
- Lu Y. The Conjunction and Disjunction Fallacies: Explanations of the Linda Problem by the Equate-to-Differentiate Model. Integr Psychol Behav Sci. 2016 Sep;50(3):507-31. doi: 10.1007/s12124-015-9314-6. PMID: 26077336; PMCID: PMC4967104.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










Süper bir yazı tesekkurler