Regiomontanus Problemi Nedir? En İyi Görüntüleme Açısı Nasıl Bulunur?

Regiomontanus, astronomi tarihinde çığır açan bir isimdi. Hazırladığı astronomik tablolar, o güne dek ulaşılamamış bir doğruluk seviyesine sahipti. Antik Yunan matematiğinin yeniden keşfinde önemli rol oynadı, küresel trigonometri alanında ise yalnızca eskileri derlemekle kalmadı, kendi katkılarıyla bu alana yenilik getirdi.

Adını hiç duymamış olabilirsiniz, ama ortaya koyduğu problemle muhtemelen hayatınızda birden çok kez karşılaştınız. Sinema salonunda en iyi koltuğu seçmeye çalışırken ya da bir fotoğraf çekerken doğru açıyı bulmaya uğraşırken aslında farkında olmadan Regiomontanus’un sorusuna yanıt arıyorsunuz.

Regiomontanus Kimdir?

Regiomontanus (Johann Müller, 1436–1476), 15. yüzyılın en etkili bilim insanlarından biridir. Genç yaşta Viyana Üniversitesi’nde astronom Georg von Peuerbach’ın öğrencisi oldu. Antik kaynakları inceleyip düzeltmekle kalmadı, gözleme dayalı çalışmalarıyla modern astronominin temellerini attı.

Peuerbach’ın ölümü üzerine Batlamyus’un Almagest adlı eserinin çeviri ve yorum işini devraldı. Kardinal Bessarion’un desteğiyle Roma’ya gitti, burada bilimsel çalışmalarını sürdürdü. Trigonometri üzerine yazdığı De triangulis omnimodis, alanın en erken ve sistematik kaynaklarından biridir.

1471’de Nürnberg’e yerleşti, bir gözlemevi ve matbaa kurdu. Gözlem araçları geliştirdi, yıldız tabloları ve takvimler yayımladı. Ephemerides adlı eseri, Kolomb ve Vespucci gibi kâşifler tarafından kullanıldı. 1476’da, Papa’nın takvim reformu için Roma’ya çağrıldı, ancak aynı yıl büyük ihtimalle veba nedeniyle hayatını kaybetti.

Regiomontanus, antik bilgiyi yeniden canlandıran, gözleme dayalı bilim anlayışını benimseyen ve bilimsel yayımcılığı başlatan öncü bir figürdür. Çalışmaları Kopernik’e ve modern bilime giden yolu açmıştır.

Yüzyıllar boyunca bir çok matematikçi Euclid’in elemanlar eserini okuyarak geometri ve matematik öğrendiler. Birçok fizikçi ve astronom ise bu kitabın metodolojisini örnek alarak alanlarıyla ilgili kitaplar yazdılar.

Regiomontanus Problemi Nedir?

1471 yılında Alman matematikçi Johann Müller Regiomontanus bir arkadaşına şöyle bir soru yönelttiği bir mektup yazdı: “Yere dik duran bir çubuk, yerin hangi noktasından bakıldığında en büyük görünür?”

Bugün bu tür bir problem cebirsel yöntemlerle kolayca çözülebilir. Ancak Regiomontanus’un zamanında modern cebir henüz yoktu; cebirin gelişmesi için yaklaşık iki yüzyıl daha geçmesi gerekecekti. Bu yüzden çözüm, tamamen geometrik yöntemlerle bulunmak zorundaydı. Üstelik, böyle bir yaklaşım sadece zarif değil, aynı zamanda oldukça sezgiseldi.

Zamanla bu temel sorunun farklı versiyonları ortaya çıktı. “Heykel problemi” ve “Ragbi problemi” gibi örnekler, Regiomontanus’un sorduğu sorunun çeşitli uyarlamalarıdır. Hepsinde temel fikir aynıdır. Bir nesnenin görüş alanındaki büyüklüğü, yani görünür açısı, nereden bakıldığında en fazla olur? Şimdi bu iki örnek üzerinden, Regiomontanus’un bu klasik problemini daha yakından inceleyelim.

Bir heykel hangi noktadan en net görünür?

Şimdi kendimizi A noktasındaki bir seyircinin yerine koyalım. Heykele oldukça yakınız, bu yüzden başımızı yukarı kaldırmak zorunda kalırız — bu hem konforsuzdur hem de görüş açımız çok dardır. Yani heykelin yalnızca küçük bir kısmını görebiliriz.

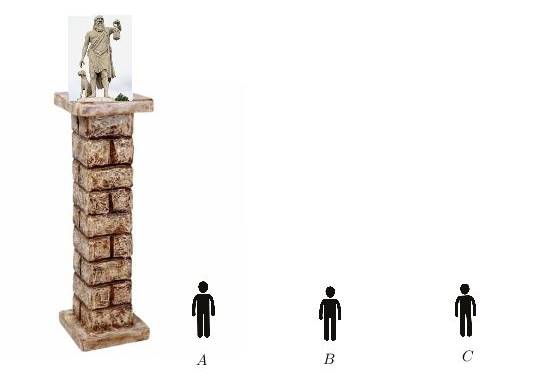
C noktasındaki bir seyirciye geçelim. Bu kez uzaklık artar, başımızı yukarı kaldırmamız gerekmez. Ancak bu sefer de heykel çok küçük görünür. Görsel detayları seçmek zorlaşır ve görüş netliği azalır.

Açıkça görüldüğü gibi, A noktası gibi çok yakın ya da C noktası gibi çok uzak olmak, heykelin ideal şekilde görünmesini engeller. En uygun nokta, bu ikisinin arasında bir yerde — yani B noktasıdır. Bu noktadan heykelin tamamını en geniş açıyla görebiliriz.

Peki bu “en iyi bakış noktası”nı yalnızca sezgilerle değil, geometriyle de bulabilir miyiz? Evet, kesinlikle.

Bu özel nokta, heykelin tepe ve taban noktalarından geçen ve görüş açısının en büyük olduğu noktayı içeren bir çember üzerindedir. Yani, bakış noktasının heykelin uç noktalarını görecek şekilde yer aldığı yer, bu iki noktayı gören en büyük çevresel açıyı sağlar. Bu ilke, Öklid’in Elementler adlı eserinin üçüncü kitabında, çemberler üzerine kurduğu temel sonuçlardan biriyle doğrudan ilişkilidir.

Bu problem, matematik tarihinde karşımıza çıkan ilk optimizasyon problemlerinden biridir. Büyük olasılıkla, Rönesans döneminin sanatçılarını meşgul eden perspektif sorularından esinlenmiştir.

Modern matematik ders kitaplarında bu problem genellikle şöyle formüle edilir. Bir tablo, bir duvara düz şekilde asılmıştır. Bu tabloyu en geniş görüş açısıyla görmek için duvardan ne kadar uzakta durmak gerekir?

Problemin başka bir versiyonu da şudur. Yere dik duran sabit bir nesne (örneğin bir çubuk, heykel ya da pano) belirli bir yükseklikte bulunur. Göz hizası sabit olan bir gözlemci bu nesneyi hangi noktadan izlerse, görüş açısı maksimum olur? Sorunun bir başka versiyonu ise aşağıdaki gibidir.

Ragbi oyuncusunun sayı yapmak için karşı kaleye en uygun mesafesi neresidir?

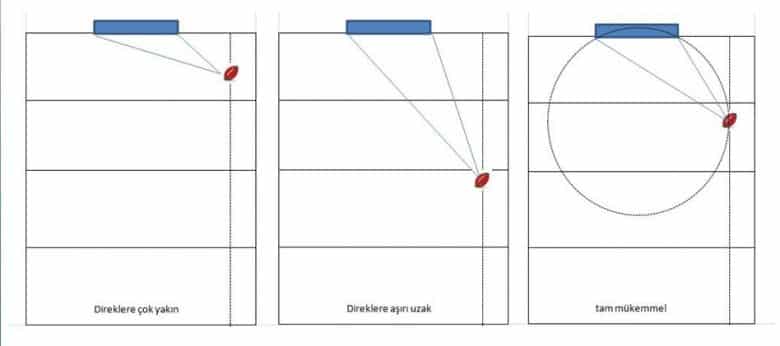
Bu soruyu çözmek için sahayı yukarıdan görmemiz, yani durumu kuş bakışı ele almamız gerekir. Kaleyi bir doğru parçası gibi düşünürsek, en geniş görüş açısını sağlayan noktayı bulmamız gerekir.

Bunun için kale direklerinin uç noktalarından geçen bir çember çizeriz. Sahada bu çemberin üzerinde kalan herhangi bir noktadan kaleye bakıldığında, kale en geniş açıyla görülür. Özellikle bu çemberin kale çizgisine dik inen ekseniyle kesiştiği nokta, atış için en ideal konumu verir. Görselde bu durum, kale direklerinden çıkan ve atış yönünü belirleyen noktalı çizgilerle gösterilmektedir.

Yukarıdaki tüm problemler, elbette cebirsel yollarla da çözülür.. Ancak Regiomontanus’un yaklaşımı, yalnızca işlevsel değil, aynı zamanda son derece yaratıcıdır.

Bu nedenle, bir dahaki sefere sinemada koltuk seçerken ya da bir manzarayı en iyi açıyla fotoğraflamak isterken bu problemi ve çözüm yöntemini hatırlayın. Doğru konumu seçtiğinizde, yalnızca daha iyi görmezsiniz. Aynı zamanda daha az çaba harcarsınız. Kısacası, geometrinin rehberliğinde zararlı çıkmazsınız. Ayrıca merak ederseniz: Standart En Boy Oranı Neden 16:9 Biçimindedir?

Kaynaklar ve ileri okumalar

1. This is a legendary problem. It is taught in calculus, but the ancients solved with only geometry. Kaynak site: Youtube. Bağlantı: This is a legendary problem. It is taught in calculus, but the ancients solved with only geometry
2. Wells, David (1998). Geometrinin Gizli Dünyası. (çev. Selçuk Alsan), (İstanbul: Sarmal Yayınevi)
3. Hadjidemetriou, Stathis. (2024). Regiomontanus angle maximization for catadioptric sensors with paraboloidal mirrors. Scientific Reports. 14. 10.1038/s41598-024-69498-x.

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel