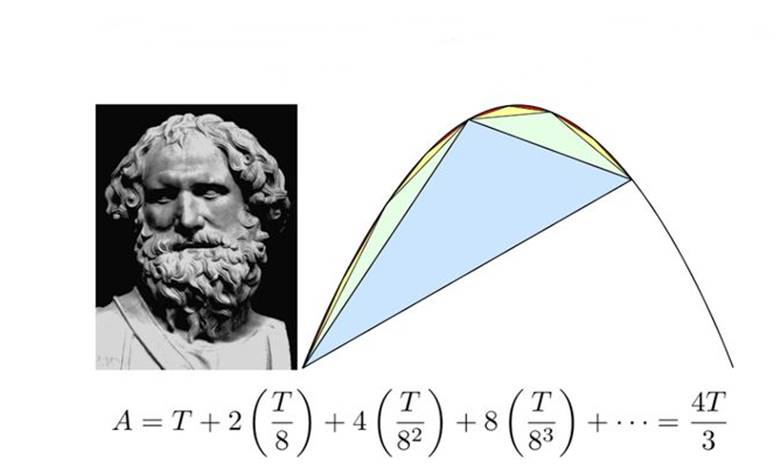
Geometrinin varoluş nedeni temelde alan hesaplarıdır. Hepimizin bildiği gibi hesaplanacak olan alan bir dikdörtgen ya da üçgen ise bu pek zorlu bir görev değildir. Ancak daha karmaşık şekiller için daha farklı tekniklere ihtiyaç vardır. Antik Yunan’da bunun için pek çok farklı yöntem geliştirilmiştir. Bunlardan en etkileyici olanlarından birisi de Arşimet tarafından yapılmıştı.
Arşimet Quadrature of a Parabola (Parabolün Dörtgenleştirilmesi) adlı eserinde herhangi bir parabol kirişi çizilerek oluşturulan kesiminin alanını bulmak için Knidoslu Eudoxus’a atfedilen tüketme yöntemini kullandı.

Günlük hayatımızda parabol, basketbolda üç sayılık atışlardan hatırlayabileceğiniz bir eğridir. Ancak bu eğri ve benzerleri aslında yalnızca yaklaşık olarak paraboliktir. Arşimet’e göre gerçek bir parabol, bir koninin bir düzlemle kesilmesiyle elde edilen bir eğri anlamına gelirdi.
Arşimet’in bir parabolün içinde kalan herhangi bir alanı bulmak için kullandığı strateji şaşırtıcıydı. Parabolik parçayı, kırık çanak çömlek parçaları gibi birbirine yapıştırılmış sonsuz sayıda üçgen parça olarak yeniden tasarladı. Çizdiği üçgenler ise belli bir boyut hiyerarşisi içindeydi. Yani bir büyük üçgen, iki küçük üçgen, dört daha küçük üçgen biçiminde devam etti.
Arşimet stratejisini gerçekleştirmek için önce tüm kırıkların alanlarını bulması gerekiyordu. Fakat bu parçalar tam olarak nasıl tanımlanacaktı? Sonuçta ilk büyük üçgeni aşağıdaki üçgenlerden herhangi biri biçiminde çizmiş olabilirdi. İşte bu noktada aklına parlak bir fikir geldi. Tüm üçgenleri kapsayacak bir model oluşturacaktı.
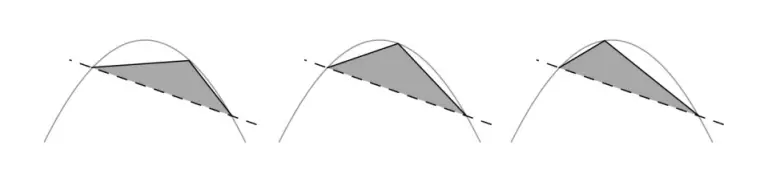
Bunun için parabolü kesen çizgiyi aldı ve parabole teğet olacak biçimde yukarıya kaydırdı. Teğet olduğu noktayı da üçgenin tepe noktası olarak kabul etti. Sonrasında da bu kuralı tüm üçgenlerini çizerken uyguladı. En sonunda çizdiği şekil muhtemelen aşağıdaki gibi olmuştur.
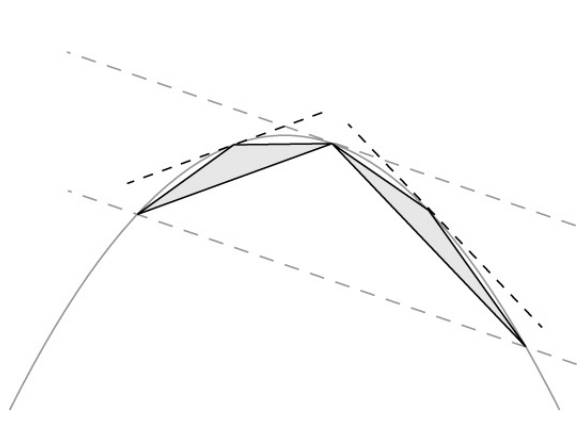
Daha sonra Arşimet, paraboller ve üçgenler hakkında bilinen geometrik gerçeklere başvurdu. Yeni oluşturulan her üçgenin, ana üçgenin sekizde biri kadar alana sahip olduğunu kanıtladı.
Tüketme Yöntemi İle Parabolün Alanının Hesaplanması
Böylece, en büyük üçgenin 1 birim alanı kapladığını söylersek o zaman onun kenarlarını taban olarak kabul eden üçgenler toplamda ⅛ + ⅛ = ¼ kadar alanı kaplar. Sonraki her aşamada da aynı kural geçerlidir.
Küçük üçgenler bir önceki büyük üçgenin her zaman dörtte biri kadar bir alanı kapatacaktır. Bir kez yapılan her zaman yinelenebilir sözü gereği bu işlemi sonsuza kadar devam ettirirsek, yani parabol kesiminin alanını tüketirsek; Alan = 1 + 1⁄4 + 1⁄16 + 1⁄64 + · · · biçiminde her terimin kendisinden önceki terimin dörtte biri olduğu sonsuz bir seri toplamı olacaktır.
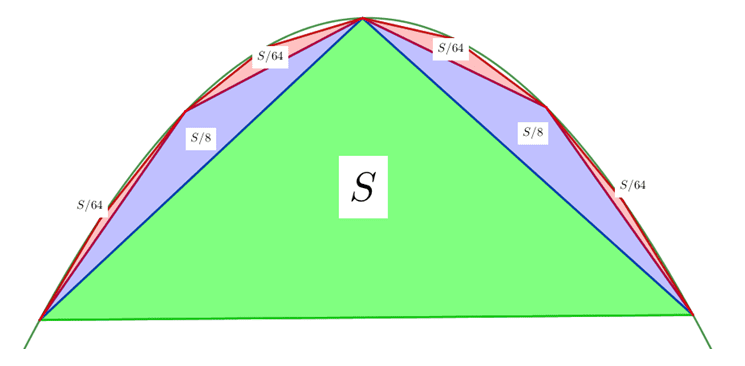
Bu sonsuz seride her terimi 4 ile çarparsak; 4. Alan= 4(1 + 1⁄4 + 1⁄16 + 1⁄64 + · · · ) = 4 + 4⁄4 + 4⁄16 + 4⁄64 + · · ·= 4 + 1 + 1⁄4 + 1⁄16 + · · ·= 4 + Alan elde ederiz. Bu durumda 4. Alan = 4 + Alan biçiminde bir sonuca ulaştık. Bunu 4x= x+ 4 gibi de düşünebiliriz. Denklemi çözünce de alanın 4/3 olduğunu buluruz. Diğer bir deyişle parabolün alanı büyük üçgenin alanının 4/3’üne sahiptir.
Arşimet’in çözümü yukarıda aktardığımızdan biraz daha farklıydı. Tüketme yöntemi yardımıyla, parabolün alanının 4/3’ten küçük veya 4/3’ten büyük olamayacağını, dolayısıyla 4/3’e eşit olması gerektiğini kanıtladı.
Arşimet’in Parabol İçin Uyguladığı Yöntem Günümüzde Yaşamaya Devam Ediyor
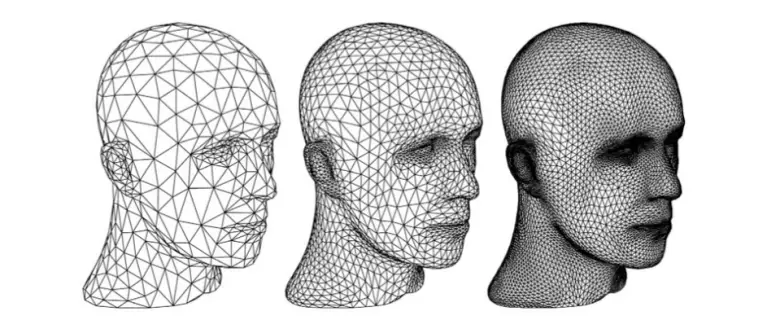
Arşimet’in mirası bugün yaşıyor. Çocuklarımızın izlemeyi sevdiği bilgisayar animasyon filmlerini düşünün. Shrek, Finding Nemo ve Toy Story gibi filmlerdeki karakterler, kısmen Arşimet anlayışını somutlaştırdıkları için gerçekçi görünmektedir. Herhangi bir yüzeyi, üçgenlerle ikna edici bir şekilde tahmin etmek mümkündür. Ne kadar çok üçgen kullanırsak ve onları ne kadar küçültürsek, yaklaşım o kadar iyi olur.
Görünüşe göre Arşimet icat ettiği vidası, savaş makineleri ile onu hatırlamamızı istemişti. Bize onlar hakkında çok az yazılı bilgi bıraktı. En çok matematiksel icatları ile övünüyordu. Arşimet’in bir matematikçi olarak güçlü yönlerinden biri, hem fiziksel hem de geometrik argümanları kullanarak problemlere oldukça farklı iki şekilde yaklaşma yeteneğiydi. ‘Çemberin Ölçümü’ isimli çalışmasında pi sayısını (3,142) çok küçük bir hatayla hesaplamayı başardı. ( Detaylar: Arşimet’in Pi Sayısını Hesaplamak İçin Kullandığı Güzel Ve Basit Yöntem)

Tüketme yöntemi ile pi sayısını hesaplama girişimi ve çokgenler yardımı ile sonsuz serilere yaklaşımı bunun en çarpıcı örneklerinden sadece bir kaçı.
Kaynaklar ve ileri okumalar
- 100 great problems of Elementary Mathematics Their History and Solutions, Heinrich Dörrie
- Archimedes’ squaring of a parabola | Famous Math Problems 6 | NJ Wildberger https://www.youtube.com/watch?v=tdvII0x0Y58
- Archimedes’ quadrature of the parabola and the method of exhaustion; Bağlantı: https://www.math.mcgill.ca/
- Steven Strogatz; Infinite Powers: How Calculus Reveals the Secrets of the Universe
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










Eskiden İzmir Anadolu öğretmen lisesi olan çiğli fen lisesinde okuyan bir öğrenci olarak eski bir mezunun makalesini okuma fırsatını yakalayacağımı hiç tahmin etmezdim.