Sosyal medyada tartışmalar farklı nedenlerden dolayı sıkça ortaya çıkar. Ancak bu tartışmanın aslında son derece basit bir matematik sorusu hakkında olması komiktir. Tartışmanın temel nedeni aşağıda gördüğünüz matematik işlemi. Cevap 1 mi yoksa 16 mı?
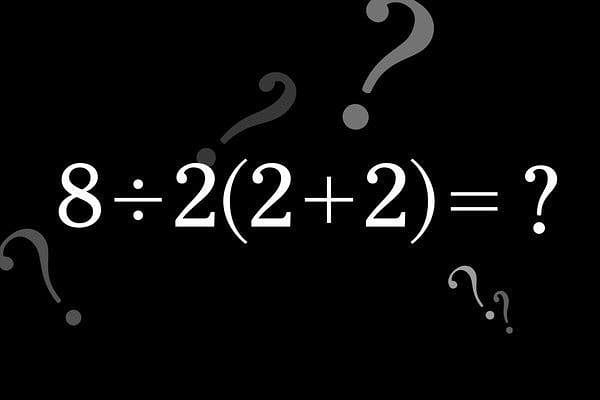
Bu soru internet ortamında hayli tartışıldı. Her iki cevabın da taraftarları çok ateşli. Aslına bakarsanız bu tarz sorular gerçekten de sosyal medya etkileşimi almak adına idealdir. Sonucunda soru çok kolaydır. Bir bakışta doğru cevabı bulduğunuzu düşünürsünüz. Ancak yorumlar kısmına baktığınız zaman kafanız karışır.
Üstelik bir hesap makinesi ile çözmek istediğiniz zamanlarda da işler daha da karışır. Bunun nedeni aşağıdaki örnekte de gördüğünüz gibi iki cevap çıkmasıdır. Sonuçta bir soru ve doğal olarak bir cevabı olması lazım. O zaman sorun nerede?

Sorun aslında iki tarafta da değil. Sorun sorunun iyi tanımlanmış olmamasında yatıyor. İyi tanımlanmış matematikte önemli bir terimdir. Esasen, belirli bir girdinin her zaman aynı çıktıyı verdiği anlamına gelir. Tüm matematik öğretmenlerinin hem fikir olduğu bir şey vardır. 8 ÷ 2( 2+2) işleminin cevabını farklı yerlere parantezler yazarak değiştirebiliriz.
Örneğin (8 ÷ 2) ( 2+2) biçiminde bir parantez yerleştirirsek cevabımız 16 çıkar. Ancak parantezi 8 ÷ ( 2( 2+ 2)) biçiminde yazarsak 8 ÷ 8 = 1 sonucuna ulaşırız. Fazladan parantezler belirsizliği ortadan kaldırır ve bu sayede sorumuz iyi tanımlanmış olur. Ancak asıl sorumuza geri dönersek, orijinalinde parantezimiz olmadığına göre hangi cevap doğrudur? diye soracaksınız. Aslında iki cevap da doğrudur. Yanlış cevap verilmesinin nedeni biraz da öğrenim biçiminiz ve temelinde yaşadığınız yer ile ilişkilidir.

İşlem Sırası Nasıldır?
Matematik okuryazarı olmak için matematikte “imla” ve “gramer” ile ilgili kuralları anlamak önemlidir. İşlem sırası olarak bilinen katı kurallar dizisi, doğru aritmetik dilbilgisini tanımlar. Bu kurallar bize, her ikisi de bir denklemde göründüğünde, toplama ve çarpma gibi matematiksel işlemleri gerçekleştirmemiz için gereken sırayı söyler.
İngilizce dilinde eğitim veren okullarda işlem sırasını öğrencilerin akıllarında tutması için öğretmenler ders anlatırken tahtaya bazen PEMDAS ( Parantheses – Exponenets – Multiplication – Division – Additon – Subtraction / Parantez, üstler, çarpma, bölme, toplama, çıkarma ) bazen de BODMAS ( Brackets – Order – Division – Multıplication – Addition – Subtraction / Parantez, üstler, bölme, çarpma, toplama, çıkarma ) yazarlar.
Öğrencilere pratiklik kazandıracağını düşünerek yapılan bu kelimeler, ilerleyen zamanda, günümüzde gördüğünüz gibi, detaylar akıldan çıktığı için kafa karışıklığına neden olabilir. Her iki kısaltma da oldukça popülerdir ve şu anda dünya çapında bunun için bir standart yoktur. ( Türkçe ‘de böyle bir kısaltma olmaması aslında bizim için bir avantajdır. Ancak yabancı dilde eğitim veren bir okulda okuduysanız siz de bu kısaltmalardan birini muhtemel öğrenmişsinizdir.) Türkçe’de müfredatta işlem sırası şu şekilde verilir.
- Eğer işlemimizde üslü ifadeler varsa önce bu ifadelerin değerini bulup yerlerine yazmalıyız.
- Devamında parantez içerisindeki işlemleri yapıp sonuçlarını bulmalıyız. Bulduğumuz sonuçları yerine yazmalıyız.
- Bir sonraki sıra çarpma veya bölme işlemlerinindir. Eğer çarpma ve bölme işlemleri yan yana ise, aralarında başka bir işlem yoksa, soldan sağa doğru işlem yapmalıyız. Yani soldan sağa doğru ilk hangisi varsa önce onu daha sonrada diğerini yapmalıyız.
- En son sıra toplama veya çıkarma işleminindir. Toplama veya çıkarma işlemlerinin sonuçlarını bulup, o işlemin veya işlemlerin yerlerine yazmalıyız. Eğer yan yana ise, aralarında başka bir işlem yoksa, soldan sağa doğru işlem yapmalıyız. Yani soldan sağa doğru ilk hangisi varsa önce onu daha sonrada diğerini yapmalıyız.
Aslına bakarsanız 8 ÷ 2 (2 + 2) ile karşılaşan kişilerin hemen hemen hepsi önce parantez içinden başlanması gerektiğini kabul etti. Bu iyi haber :) Bu durumda parantezin içindeki sayının da 4 çıktığını düşünürsek soru 8 ÷ 2 × 4 seviyesine indi. Ve işler bu noktada karışmaya başladı.
İşlem Sırasında Tanımımıza Göre Bölme Önceliklidir
Önce bölme işlemini yaparsak, 4 × 4 = 16 sonucunu elde ederiz ancak önce çarpma işlemini yaparsak sonucumuz 8 ÷ 8 = 1 olur. Peki, ama hangisi doğru? Yukarıdaki 6. sınıf ders notunu anımsayalım. Ne deniyordu? “Eğer çarpma ve bölme işlemleri yan yana ise, aralarında başka bir işlem yoksa, soldan sağa doğru işlem yapmalıyız.” İşte bu sebepten dolayı cevaba 16 diyebiliriz. Ancak bu noktada yine size itiraz edenler çıkacaktır ve aslında haklılardır.
8 ÷ 2 (2 + 2) ifadesinde çarpmanın toplama üzerinde dağılma özelliğini uyguladığımızı düşünelim. Bu durumda işlemimiz 8 ÷ (4 + 4) olacaktır. İşlem sırası önce parantezden başlamamızı söylüyor. Buna göre parantezin içini yaparsak 8 ÷ 8= 1 sonucunu elde ederiz. Bu bir sorundur.
Sonucunda a(b) ifadesini (a x b) biçiminde düşünebiliriz. Ancak a(b) ifadesi için (ab) demek de yanlış değildir. Bu nedenle bir çok bilim insanı bu soruyu belirsiz olarak kabul ediyor ve bunun çözümü için de bize daha fazla parantez eklememizi öneriyor. Sonuçta bir dilde virgülü nereye yerleştirdiğimiz cümlenin anlamını etkiler. Aynı şey matematik için de geçerlidir. Fazladan parantezler belirsizliği ortadan kaldırır ve bu sayede sorumuz iyi tanımlanmış olur.
Sorunun Cevabını Hesap Makinaları Neden Farklı Buldu?

Son olarak akla gelen bir sorunun daha açıklamasını yapalım. Üstteki görselde gördüğünüz hesap makineleri neden iki farklı cevap vermişti? Bunun nedenini hesap makinelerinin farklı markalar olmasına bağlayabilirsiniz. Ancak aynı denemeyi biz de yaptık…
Soldaki ilk cevabın hatalı çıkmasının nedeni yazılımsal, yani bazı hesap makineleri boşluğu çarpma olarak algılamıyor ve sağda görebileceğiniz gibi illa çarpı işaretinin konmasını istiyor. Yazının başında örnek verdiğimiz iki hesap makinesi farklı markalardı. Onlar sadece problemle ilgili mevcut anlaşmazlığı yansıtıyorlardı. Bir gün matematik öğretmenlerinin hepsi bir cevap üzerinde birleşirse, programcılar da onları takip edeceklerdir.
Matematikçilerin uzlaşamadığı pek çok konu vardır. İşte size bir tartışma konusu daha en küçük doğal sayı kaçtır? İlginç bir biçimde dünyanın farklı yerlerinde bu soruya farklı cevaplar alırsınız. Kimisi için doğal sayılar 1 ile başlar, kimisi için de 0. Bu tartışmayı da merak ederseniz detaylar burada: Sıfır Bir Doğal Sayı mıdır? Yoksa Değil midir?. Umarız bu açıklamalar tartışmaya son verir, hadi barışalım :)
Kaynaklar ve ileri okumalar için:
- The Math Equation That Tried to Stump the Internet; Yayınlanma tarihi: 2 Ağustos 2019; Bağlantı: The Math Equation That Tried to Stump the Internet;
- The PEMDAS Paradox; yayınlanma tarihi: 17 Haziran 2019; Bağlantı: The PEMDAS Paradox/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel