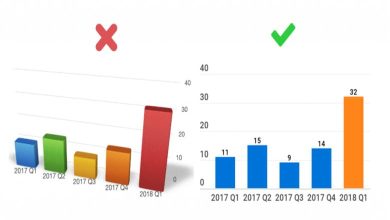
Günümüzde artık birçok kişi Fibonacci dizisinin adını bir şekilde duymuştur. Bu durumda, onun daha genel hâli olan N-bonacci dizisiyle tanışma zamanı gelmiş demektir.

Ünlü Fibonacci dizisinin bir kısmı 0,1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144…biçimindedir. Bir sonraki rakamı merak ederseniz de aslında yapmanız gereken son derece basit bir toplama işlemidir. Çünkü Fibonacci dizisindeki her sayı kendisinden önceki iki sayının toplamıdır. Bu sayede bu diziyi istediğiniz kadar uzatmanız mümkündür.
Bu dizi adını İtalyan Leonardo Bigollo Pisano’dan alır. (1170 – 1250). Kendisi Orta Çağ’ın en yetenekli Batılı matematikçisi olarak kabul edimektedir. Ancak biz kendisini daha çok ‘Fibonacci’ lakabıyla, yani ‘Bonaccio’nun oğlu’ olarak biliriz. Fibonacci Dizisinin bu kadar bilinmesinin temel nedeni biraz da bu dizinin altın oran ile olan ilişkisi sonucudur.

Aslında Leonardo Fibonacci bu sayılar için ‘Fibonacci serisi’ veya ‘Fibonacci sayıları’ terimini kullanmamıştı. Muhtemelen adının ölümünün ardından anımsanacağının da farkında değildi. Diziye adını veren on dokuzuncu yüzyıl Fransız matematikçisi François Édouard Anatole Lucas oldu.
Kendisi, hayranı olduğu bu diziye sadece adını vermekle kalmadı. Aynı zamanda dizinin rakamlarıyla oynayarak farklı diziler de oluşturdu. Bu çalışmalar sayesinde günümüzde adı Lucas sayılarıyla birlikte anılmaktadır.
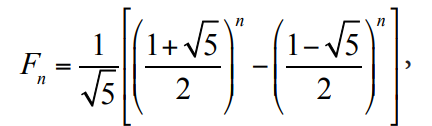
Daha sonra, Fransız matematikçi Jacques Philippe Marie Binet (1786–1856), dizideki herhangi bir konumdaki Fibonacci sayısını doğrudan hesaplamaya yarayan bir formül geliştirdi. Bu formül, dizinin yapısını daha derinlemesine anlamamıza olanak tanıdı ve matematiksel olarak Fibonacci dizisini daha güçlü bir şekilde ifade etmemizi sağladı.
N-bonacci Dizisi Nedir?
“Bunları zaten biliyoruz” diyorsanız, sizi daha ilginç birkaç diziyle tanıştıralım. Örneğin, 3-bonacci dizisi buna güzel bir örnektir. Bu diziyi oluşturmak için 0, 0 ve 1 sayılarıyla başlayın. Sonrasında her terimi, kendisinden önce gelen üç terimin toplamı ile elde edin. Bu şekilde diziniz şöyle görünür: 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149…
İsterseniz biraz daha ileri gidelim ve bu kez 4-bonacci dizisini oluşturalım. Bu dizide başlangıç değerleri 0, 0, 0 ve 1’dir. Sonraki her terim, önceki dört terimin toplamı ile elde edilir. Ortaya çıkan dizi: 0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208…
Buraya kadar gelmişken neden duralım? Şimdi de N-bonacci dizisini tanımlayalım. N-bonacci Dizisi, yazının başında söz ettiğimiz Fibonacci dizisinin genellemesidir. Dizi, N tane sıfırla başlar, ardından bir gelir. Sonraki her terim, kendisinden önce gelen N terimin toplamıdır. Bu tanım altında:
- 1-bonacci dizisi: yalnızca 1’lerden oluşur.
- 2-bonacci dizisi, yani Fibonacci dizisi: her terim, önceki iki terimin toplamıdır.
Fibonacci dizisinin ilginç bir özelliği daha vardır. Her terimi, kendisinden önceki terime bölerseniz bir oran dizisi elde edersiniz: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21…
Bu oranların ondalık karşılıklarına baktığınızda, sayıların Altın Oran’a (yaklaşık 1.618) giderek yaklaştığını fark edersiniz. Fibonacci dizisinin Altın Oran’la olan bağlantısı da tam olarak burada ortaya çıkar.
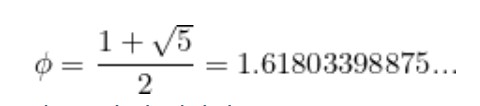
Aslında benzer sabitleri, N-bonacci dizileri için de aynı yöntemle bulmanız mümkündür. Elde edeceğiniz sonuçlar Altın Oran kadar estetik ya da etkileyici görünmeyebilir, ancak matematikçiler açısından bu sabitler son derece anlamlıdır.
Herhangi bir N doğal sayısı için, o N-bonacci dizisine karşılık gelen sabiti bulmak istiyorsanız, şu denklemi çözmeniz yeterlidir: x + (1 / x)ᴺ = 2

Bu denklemi çözdüğünüzde elde ettiğiniz x değeri, sizin N-bonacci sabitiniz olur. Fibonacci dizisi için (yani N = 2), bu sabit Altın Oran’dır. N arttıkça elde edilen sabitler farklılaşır ama her biri, dizinin uzun vadeli davranışını belirleyen temel bir rol oynar.
Infinacci Dizisi
Madem başladık, neden burada bırakalım? N’nin sonsuza gittiği durumda, yani infinacci dizisi söz konusu olduğunda işler ilginçleşir. Bu dizi, sonsuz sayıda 0 ile başlar ve ardından 1 gelir. Sonraki her terim, kendinden önce gelen tüm terimlerin toplamına eşittir. İlk birkaç adımı inceleyelim:
- …0, 0, 0, 0, 1
- Sonraki terim: (sonsuz tane 0) + 1 = 1
- Sonraki terim: 0 + 1 + 1 = 2
- Sonraki terim: 0 + 1 + 1 + 2 = 4
- Sonraki terim: 0 + 1 + 1 + 2 + 4 = 8
Bu şekilde gidersek dizinin şu şekilde devam ettiğini görürüz: 1, 1, 2, 4, 8, 16, 32, 64…
Yani infinacci dizisi, 2’nin kuvvetleri şeklinde ilerler. Her terim, kendisinden önce gelen tüm terimlerin toplamıdır. Bu toplam, her adımda bir öncekinin iki katıdır. Peki bu dizinin ardışık terimlerinin oranı nedir? Başlangıçtaki sonsuz sayıdaki sıfır terimi oranlamaya katamayacağımız için onları atlarız. Kalan diziye bakarsak:
- 1 / 1 = 1
- 2 / 1 = 2
- 4 / 2 = 2
- 8 / 4 = 2
- 16 / 8 = 2 … şeklinde devam eder
Bu nedenle, her ardışık terim çifti arasındaki oran 2’dir. Yani infinacci dizisinin uzun vadeli davranışı, sabit bir oranla—2 ile—tanımlanır. Bu oran da dizinin limiti olarak düşünülebilir. Başka bir deyişle, infinacci dizisinin sabiti 2’dir.
Sonuç olarak;
Tüm bu okuduklarınızın sonunda “Bunlar gerçekten bir işe yarar mı?” diye sormuş olabilirsiniz. Ama bazen, beklenmedik bilgiler, beklenmedik zamanlarda işe yarar.
Fibonacci dizisini biliyorsanız, bu dizinin varsayımsal bir tavşan popülasyonu problemiyle ortaya çıktığını da duymuş olabilirsiniz. Benzer bir durum Tribonacci dizisi için de geçerlidir. İlginçtir ki, Charles Darwin’in oğlu George H. Darwin, yaptığı bir hesaplamayla fillerin popülasyon artışını modellemeye çalışmıştır. Ve bu modellemede ortaya çıkan sayılar, Tribonacci dizisiyle örtüşmektedir.
Yani, sayı dizileri yalnızca soyut matematik oyunları değildir. Doğayı anlamak, sistemleri modellemek ve bazen de canlıların çoğalmasını tahmin etmek için beklenmedik şekilde karşımıza çıkabilirler.
Kaynaklar ve İleri okumalar
- Generalizations of Fibonacci numbers; Bağlantı: https://en.wikipedia.org/
- Maths in a minute: N-bonacci sequences; Yayınlanma tarihi: 14 Temmuz 2020; Bağlantı: https://plus.maths.org/
- Podani, J., Kun, Á. & Szilágyi, A. How Fast Does Darwin’s Elephant Population Grow?. J Hist Biol 51, 259–281 (2018). https://doi.org/10.1007/s10739-017-9488-5
- Bai, Shiwei & Niu, Min. (2022). The visibility graph of n-bonacci sequence. Chaos, Solitons & Fractals. 163. 112500. 10.1016/j.chaos.2022.112500.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel