Matematikçilere en sevdikleri formül sorulduğunda, çoğu zaman verilen yanıt Euler formülüdür. Ünlü fizikçi Richard Feynman da bu formülden derslerinde “matematiğin en dikkat çekici formülü” olarak söz etmiştir. Peki, bu formül neden bu kadar önemlidir?
Matematikçiler için bir denklem, bir sanat eseridir. Onun güzelliği; sadeliğinde, derinliğinde, işlevselliğinde ve farklı matematik alanları arasında kurduğu şaşırtıcı bağlarda yatar. Bazen tek bir formül, tüm bir düşünce dünyasını birbirine bağlar. Euler formülü de bu etkiye sahip nadir örneklerden biridir
1707 yılında İsviçre’de doğan Leonhard Euler, matematik tarihinin en üretken ve etkili isimlerinden biridir. Yaşamının büyük bölümünü Rusya’nın St. Petersburg kentinde geçirmiştir. Çalışmaları hem derinliği hem de özgünlüğüyle dikkat çeker. Matematikteki etkisi, edebiyatta Shakespeare’in, müzikte Bach’ın ve resimde Rembrandt’ın etkisiyle kıyaslanır.

Euler Özdeşliği Nedir?
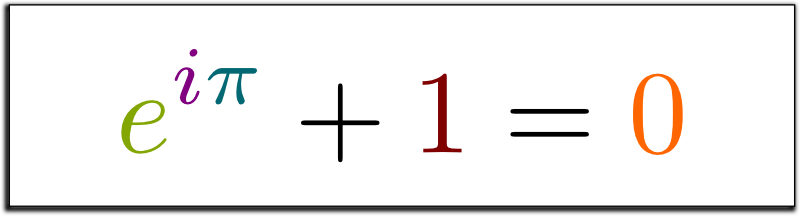
Karmaşık sayılar, hatta onların daha geniş hali olan hiper karmaşık sayılar, özel bir özelliğe sahiptir: Birbirleriyle çarpıldıklarında, bu işlem geometrik olarak bir dönmeye (rotasyona) karşılık gelir. İşte bu dönme özelliği, pek çok alanda son derece faydalıdır.
Aşağıdaki örnekte, beş karmaşık sayı ile bir “ev şekli” oluşturmuştur. Bu ev şeklini oluşturan her bir karmaşık sayı, 4 + 3i ile çarpılmış ve ardından yeniden çizilmiştir. Bu işlem sırasında her bir nokta hem dönmüş hem de orantılı olarak büyümüştür.
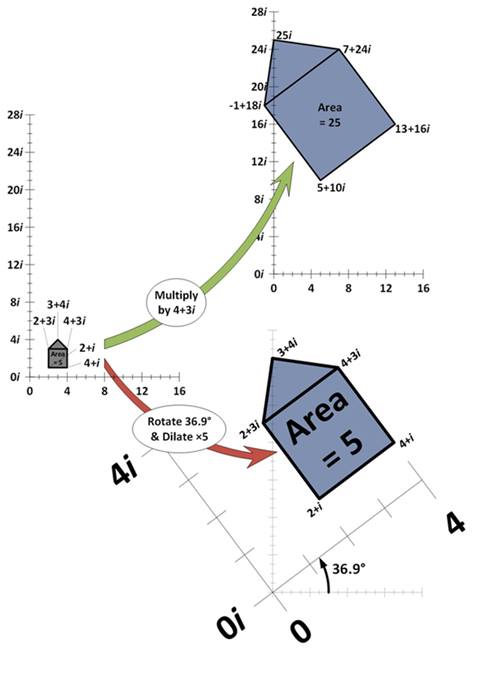
Dönme ve büyüme miktarı, çarpılan karmaşık sayının özelliklerine bağlıdır. Örneğin 4 + 3i sayısı, orijinden 5 birim uzaklıktadır ve yatay eksenle 36,9 derecelik bir açı yapar. Bu iki bilgi karmaşık sayıların kutupsal gösteriminde (r·e(iφ) ) kullanılır. Burada r uzaklığı (yani büyüklüğü), φ ise açıyı gösterir. Bu durumda sayı 5 · e (i·36,9°) biçiminde olur.
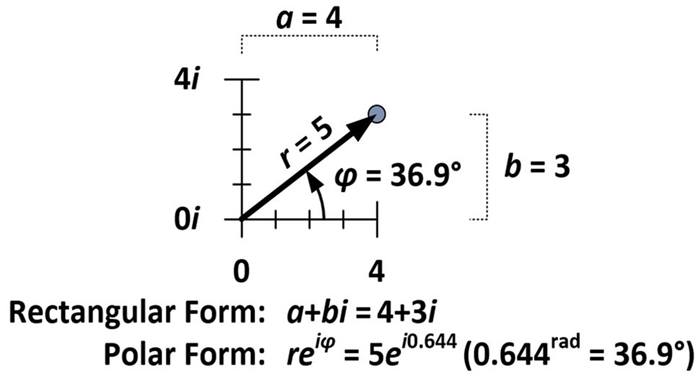
Kutupsal formda açılar radyan cinsindendir. Bir radyan, yaklaşık olarak 57,3 dereceye eşittir. 4 + 3i sayısının açı ölçüsü 0.644 radyan’dır (yani 36,9° = 0.644 rad). Bu durumda, sayının kutupsal gösterimi şöyle olur: 5 · e (i·0.644)
Karmaşık sayıların kutupsal formu tanımlandıktan sonra, Euler özdeşliği bunun özel bir durumu olarak ortaya çıkar. Burada a + bi biçimindeki karmaşık sayı için a = -1 ve b = 0 alınır. Yani bu sayı, karmaşık düzlemde negatif reel eksen üzerinde yer alır.
Kutupsal gösterim olan reiφ ifadesine göre bu durumda r = 1 olur, çünkü sayı orijinden bir birim uzaklıktadır. Bu yön eksenle π radyanlık (180 derece) açı yapar. Sonuç olarak, e(iπ) = -1 olur. Her iki tarafa 1 eklenirse, e^(iπ) + 1 = 0 elde edilecektir. Bu ifade Euler özdeşliğidir.
Euler Formülü Nedir?
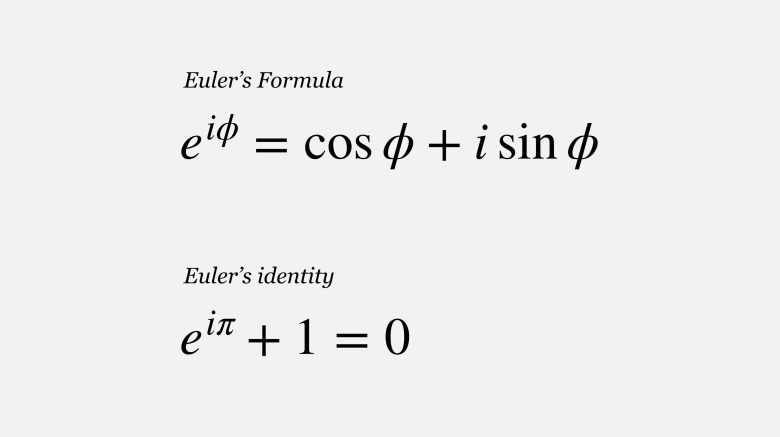
Euler özdeşliği, karmaşık analizde temel bir denklem olan Euler formülünün özel bir halidir. Leonhard Euler bu formülü 1744 yılında ortaya koydu. Kalkülüs bilgisi olmadan bu formülü anlamak mümkün değildir.
Karmaşık bir sayı olan a + bi, trigonometrik ilişkiler kullanılarak (r·cosφ) + (r·sinφ)i biçiminde yazılır. Bu ifadede r’yi ortak çarpan olarak dışarı aldığımızda, r·(cosφ + i·sinφ) elde ederiz. Bazı kaynaklar cosφ + i·sinφ ifadesini kısaca cisφ biçiminde gösterir.
cisφ ile e iφ ifadesi arasında bir eşitlik vardır. Bu eşitlik sezgisel olarak anlaşılır ancak bağlantı, türev, limit ve seri açılımları gibi analiz araçlarıyla matematiksel olarak kanıtlanır. Aşağıda bunun nasıl olacağını iki farklı biçimde inceleyebilirsiniz.

Sonuç olarak
Euler formülü, ilk bakışta akıl almaz bir bağlantıyı ortaya koyar. Döngülerin ve dalgaların simgesi olan sinüs ve kosinüs fonksiyonlarının, büyüme ve azalma süreçlerini tanımlayan üstel fonksiyonla gizli bir akrabalığı olduğunu söyler. Nobel ödüllü fizikçi Richard Feynman, bu formül için bu nedenle “matematiğin en dikkat çekici formülü” demiştir.
Euler özdeşliği de matematiğin en ünlü ve temel sayılarını bir araya getirir: 0, 1, π, i ve e. Her biri, matematiğin farklı bir alanını temsil eder. Bu açıdan bakıldığında yalnızca bir eşitlik değil; matematiğin bütünlüğüne işaret eden etkileyici bir kesişim noktasıdır.
Kaynaklar ve ileri okumalar:
- How Infinite Series Reveal the Unity of Mathematics. Yayınlanma tarihi: 24 Ocak 2022. Kaynak site: Quanta Magazine. Bağlantı: How Infinite Series Reveal the Unity of Mathematics
- Euler’s Identity: ‘The Most Beautiful Equation’. Yaınlanma tarihi: 1 Temmuz 2015. Bağlantı: Euler’s Identity: ‘The Most Beautiful Equation’
- Euler’s formula; Yayınlanma tarihi: 6 temmuz 2021; Bağlantı: Euler’s formula/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





