İçi boş bir küreyi herhangi bir yerini kesmeden ters yüz edebildiğinizi düşünün. Bu mümkün olmaz demeyin. Topoloji ile bu mümkündür. Peki ama adını son yıllarda oldukça sık duymaya başladığımız Topoloji tam olarak nedir?

Topoloji Nedir?
Topoloji, Yunanca’da yüzey veya uzay anlamına gelen topos ve bilim anlamına gelen logos kelimelerinden ortaya çıktı. Basit bir ifadeyle, ölçümler olmadan şekillerin incelenmesidir. Klasik geometride, bir şekli kaydırır, yansıtır veya döndürürsünüz. Sonucunda elde edeceğiniz şekiller birbirine eş şekiller olacaktır. Önemli olan açı ve uzunlukların değişmemesidir.
Ancak topoloji için bu gibi durumlar fazla önemli değildir. Topoloji, şeyler arasındaki ilişkilerin farklı bir şekilde anlaşılmasını sağlar. Topoloji, kesmeden, delmeden veya birbirine yapışmadan sürekli gerdirme veya bükme yoluyla şekillerin birbirine dönüşümleri ile ilgilenir. Hatta bu yüzden topolojiye bazen “lastik levha geometrisi” de denir.

Topolojide bir küp, bir piramit ve bir küre aynı şeydir. Konuya ilişkin ünlü bir örnek, bir çöreğin topolojik olarak bir kahve fincanı ile aynı şey olmasıdır. Bu dönüşümde korunan şey deliktir. Çöreğin ortasındaki delik, bardağın sapındaki delik olur.
Diğer bir deyişle, delik yok olmaz. Oysa ki aynı durum bir küre için geçerli değildir. Çünkü herhangi bir deliği yoktur. Bu nedenle bir küreyi kesmeden bir çörek haline getiremezsiniz. Bir nesnedeki deliklerin sayısı topolojide önemli bir kavramdır. Çünkü delik sayısı düzgün dönüşümlerde korunmaktadır.
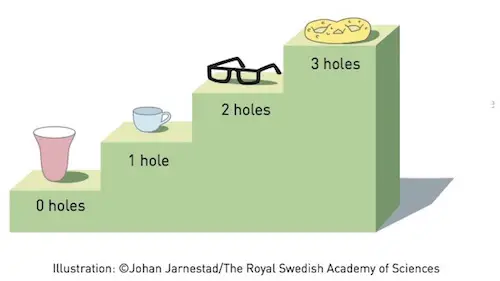
cinsi denir
Örneğin, “O” harfi, “A” harfi ve “9” sayısı topolojik olarak aynı şeylerdir. Çünkü hepsi bir delik içermektedir. Ancak “8” sayısı iki delik içerdiği için farklıdır. İki nesnenin birbiri ile aynı olması bu nesnelerdeki delik sayısı birbirine eşit olmalıdır. Topoloji, dönüşümler durumunda delik gibi hangi özelliklerin değişmez olduğuyla ilgilenir.
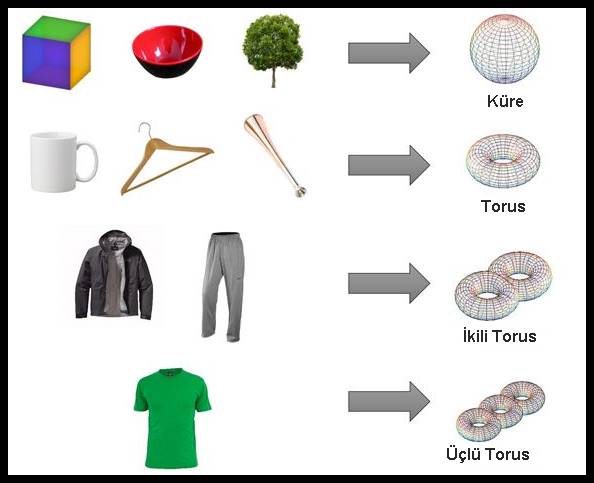
Şekilleri Topolojik Olarak Sıralamamızda Euler Karakteristiği Nedir?
Topoloji tanımı ortaya konulmadan önce, elbette bazı öncül adımlar gerekli idi. İlk hamle Euler’den geldi. 1750’de Leonhard Euler tüm çokyüzlülerin temel bazı özellikleri paylaştığını öne sürdü. Bunun sonucunda kendi adıyla anılan “Euler’in Çokyüzlüler Formülü”nü ortaya koydu.
Bu formül V + F – E biçimindedir. Burada V köşe sayısı, F yüz sayısı ve E kenar sayısıdır. Formül, tüm çokyüzlülerin temel özellikleri paylaştığını öne sürmektedir. Beş platonik cismin (bir tür düzgün çokgenden yapılan 3 boyutlu şekiller) tümü topolojik açıdan bir küreye eş değer olduğundan, hepsinin bir Euler karakteristiği ikidir.
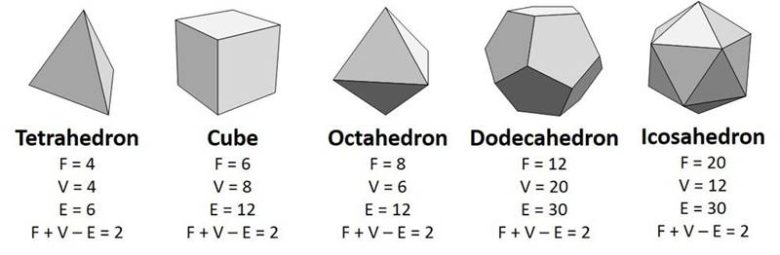
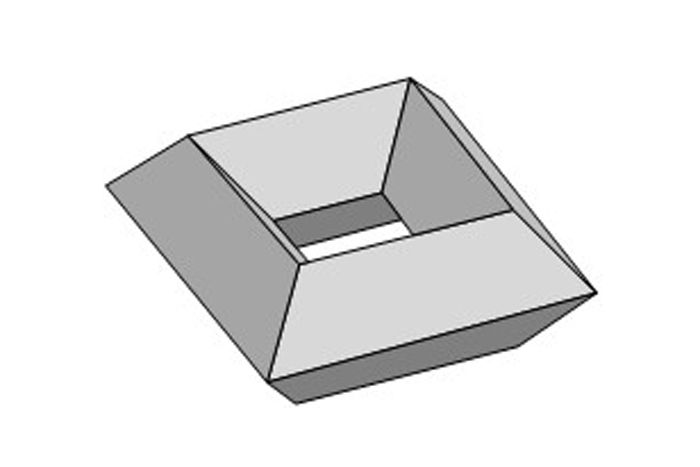
Ancak, 1813’te bir başka İsviçreli matematikçi Simone L’Huilier, Euler’in formülünün tüm çokyüzlüler için doğru olmadığını kanıtladı. Bu formül içinde delik içeren ve dışbükey olmayan çokyüzlüler için yanlış sonuç veriyordu. Gerçekten de içinde delik içeren şekillerin Euler karakteristiği ikiden farklıdır. Örneğin aşağıdaki şekle bir göz atalım. Bu şekilde F=16, V=16 ve E=32 biçimindedir. Tüm bunları V + F – E işleminde yerine yazarsanız sıfır sonucunu elde ederseniz. Aslına bakarsanız her ek delik, Euler karakteristiğini iki azaltır.
19.yy ortalarına kadar topoloji kendi başına bir araştırma konusu olamadı. 1904’te Henri Poincaré, Evrenin şeklini anlamak için topolojik bir temel oluşturmaya yardımcı olacak bir teori üreterek topolojiye somut bir gerçeklik kazandırdı.
Topoloji Ne İşe Yarar?
Topoloji günümüzde bilimin her alanında karşımıza çıkmaktadır. Örneğin, genetik ve moleküler biyoloji gibi alanlarda, belirli enzimler tarafından DNA çevresinde oluşturulan düğümlerin çözülmesine yardımcı olmak gibi çeşitli uygulamaları vardır. Ayrıca topoloji, sicim teorisini tanımlamak veya gözlemlenen verilere uyan evrenin şeklinin modellerini oluşturmak için fizikte ayrı bir öneme sahiptir.
Topoloji, bilgisayar ağ sistemlerinin tasarlanmasında da kritik önem taşır. İş istasyonlarının, anahtarların ve sunucuların düzeni, ağın fiziksel topolojisini oluşturur. Bu veri iletme kapasitesini ve hızını büyük ölçüde etkiler. Ayrıca aşağıdaki bağlantılar aracılığı ile başka kullanım alanları hakkında da fikir edinebilirsiniz.
Topolojiye giriş amacıyla yazdığımız bu yazımızda kısaca topoloji nedir sorusuna cevap vermeye çalıştık. Konu ilginizi çekti ise, birbirinden ilginç özellikler ile tanışmaya hazır olun. Şimdi de kısaca topoloji ile ilgili ünlü problemlere göz atalım
Topolojideki Ünlü Problemler Nedir?
Königsberg’in Yedi Köprüsü: Genellikle topolojideki ilk problem olarak kabul edilir. Probleminin çözümünü, 1735’te Euler tarafından yapılmış ve bu sayede de matematiğe çizge/ graf teorisi adı verilen yeni bir çalışma alanı kazandırmıştır. Detaylar: Königsberg Köprüsü Problemi Matematiği Nasıl Değiştirdi?
Avuç İçi ve Parmak İzlerindeki Desenler: Parmak izlerinin tümü, döngüler ve triradii (üç çizginin bir araya gelmesi) gibi ortak özelliklere sahiptir. 1965’te İngiliz tıbbi genetikçi Lionel Penrose, parmak izlerinin ve avuç izlerinin evrensel bir kurala uyduğuna dikkat çekti. Penrose’un kuralına göre, bir eldeki triradiuslarla, ilmekler arasındaki fark, eldeki parmak sayısından bir eksik. Detaylar burada: İnsan Vücudu Ve Parmak İzimizdeki Topoloji
Hairy Ball Yani Saçlı Top Teoremi: Herhangi bir topun tüm yüzeyinin tüylerle kapladığınızı düşünün. Şimdi elinize bir tarak alarak bu topun üzerindeki tüyleri taramaya çalışın. Cebirsel topolojide var olan Hairy Ball yani Tüylü ya da Saçlı Top Teoremine göre bu tüylerin bir kısmı eninde sonunda yine havaya kalkacaktır. Detaylar için: Adı Gibi İlginç Bir Teorem: Hairy Ball Yani Saçlı Top Teoremi
Düğüm Teorisi: Düğümlerin matematik ve bilimde özel bir önemi vardır. Çünkü özellikleri, DNA’nın biyokimyası, yeni malzemelerin sentezi ve üç boyutlu uzayların geometrisi kadar geniş bir yelpazede yer alan konularda saklı sırların açığa çıkmasına yardımcı olmaktadır. Düğüm teorisinin ana odak noktası, iki farklı görünen düğümün homeomorfik olup olmadığını belirlemektir. Detaylar: Düğüm Teorisi Nedir?
Poincaré Sanısı: Bu yazıda sadece 2 boyutlu uzayları inceledik ama garip şekillerde birbirine bağlanan 3 boyutlu uzaylar da var. “Basitçe bağlı, kapalı her 3-manifoldunun 3-küreye homeomorfik olduğunu” belirtir. Topolojinin en büyük problemlerinden biri olan Poincaré sanısı, ödüllü Yedi Milenyum Probleminden birisiydi ve çözülen ilki oldu.
Kaynaklar ve ileri okumalar için:
- The mathematical shapes in your brain; yayınlanma tarihi: Bağlantı: https://plus.maths.org/
- Maths in a minute: Topology. Yayınlanma tarihi: 23 Mart 2022; Bağlantı: https://plus.maths.org/
- What Is Topology? yayınlanma tarihi: 23 Temmuz 2015; Bağlantı: https://www.livescience.com/51307-topology.html
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel