Nehir kıyısında yapılan bir yürüyüş, matematiğin iki yeni alanının doğmasına neden olabilir mi? Eğer bu yürüyüşü yapan kişi Leonhard Euler ise, cevabı tereddütsüz bir şekilde “evet” olur.
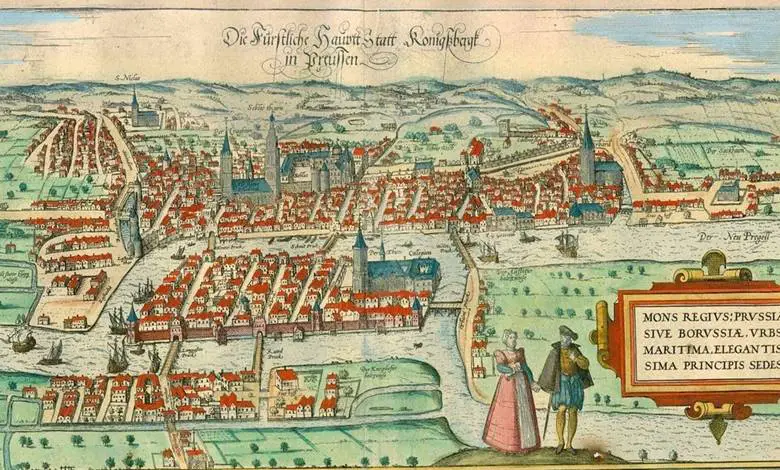
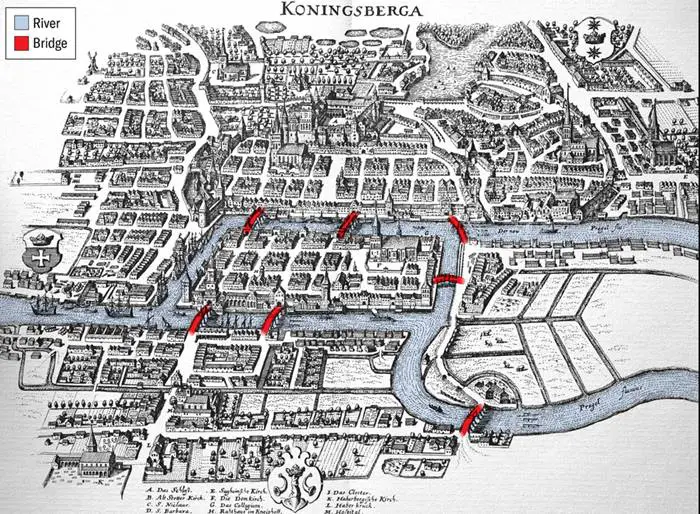
Bugün Rusya’ya bağlı Kaliningrad’ın gri ve kasvetli görüntüsünü izlemek, buranın matematik tarihinde bu denli önemli bir rol oynadığını düşünmeyi zorlaştıracaktır. Ancak 18. yüzyılda, bu şehir Prusya’nın Königsberg kenti olarak bambaşka bir kimliğe sahipti. Pregel Nehri şehrin içinden geçiyor, iki büyük adayı birbirinden ayırıyor ve bu adaları anakaraya yedi farklı köprüyle bağlıyordu.
O dönemde şehir sakinleri, şehirdeki yedi köprünün her birinden yalnızca bir kez geçerek tamamlanacak bir yürüyüş rotası oluşturmaya çalışıyordu. Ancak nehir üzerindeki iki büyük adanın etrafına kurulu bu sistemde, hangi yolu denerlerse denesinler, mutlaka bir köprüden ikinci kez geçmek zorunda kalıyorlardı.
Bu konu, zamanla yerel düşünürlerin ilgisini o kadar çok çekti ki, sonunda ünlü matematikçi Leonhard Euler’e mektup yazarak bu duruma bir açıklık getirmesini istediler. Euler başlangıçta bu talebi ciddiye almadı. Hatta bu problemin “matematikle pek ilgisi olmadığını” belirterek isteği küçümseyici bir dille geri çevirdi. Ancak zamanla merakı ağır bastı. Euler, yedi köprü problemini ele aldı ve çözüme ulaştı. Bunu yaparken, matematik tarihinde daha önce var olmayan iki alanın temellerini de atmış oldu.
Königsberg Köprüsü Problemi Neden Önemlidir?
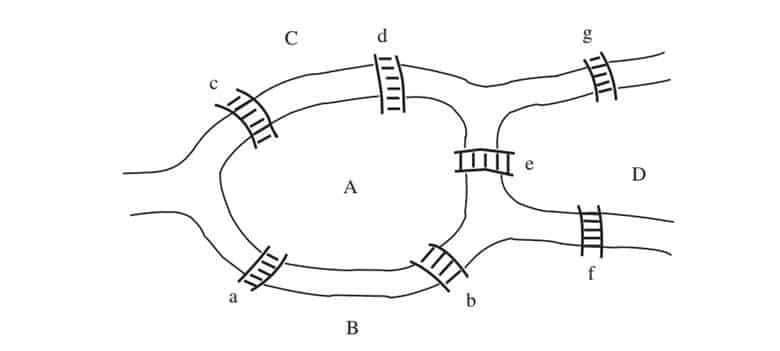
Her matematiksel problemi çözmeye başlamadan önce, gereksiz ayrıntıları ayıklamak gerekir. Geriye sadece problemi tanımlayan temel unsurlar kalmalıdır. Bu işleme soyutlama denir. Yedi köprü probleminde köprülerin ne kadar uzun olduğu, adaların yüzölçümü ya da haritanın hangi yöne baktığı gibi detaylar, çözüm açısından hiçbir şey değiştirmez. Önemli olan tek şey, kara parçalarının birbirine kaç köprüyle bağlı olduğudur.
Bu soyutlama yapıldığında, karmaşık bir harita artık yerini basit bir diyagrama bırakır. Kara parçaları artık birer çember, köprüler ise bu çemberleri birbirine bağlayan çizgilerdir. Böylece elimizde artık bir harita değil, üzerinde düşünülmesi gereken bir çizge—yani bir grafik—vardır. İşte Euler’in asıl devrimi de tam burada başlar.
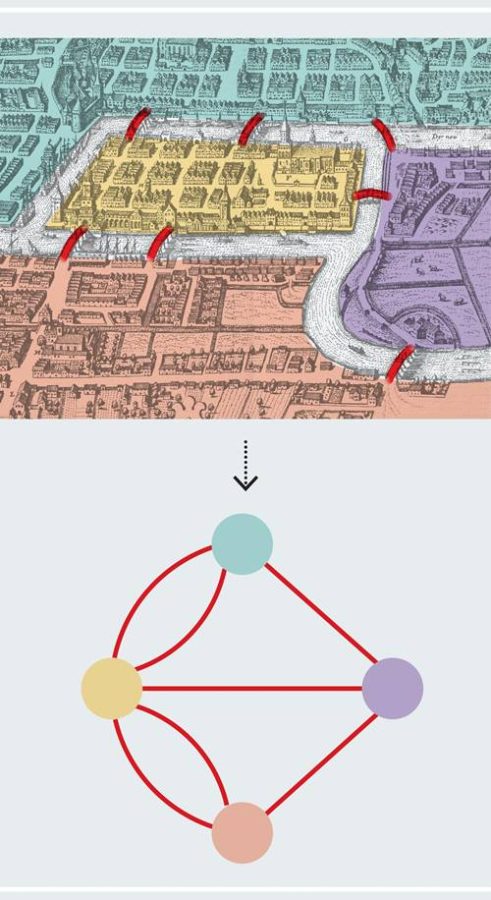
Modern matematikte, bu tür diyagramlara “graf” ya da “çizge” denir. Ancak bu kavram, genellikle x-y düzlemindeki eğriler ya da çubuk grafik gibi istatistiksel görsellerle karıştırılmaktadır. Bu nedenle, bazı durumlarda “ağ (network)” ifadesi daha açıklayıcı olur.
Çizge diyagramlarında, her çember bir “düğüm” (ya da “köşe”), bu düğümleri birleştiren çizgilere ise “kenar” denir. Çizgelerin temsil ettiği şeyler köprülerle ya da kara parçalarıyla sınırlı kalmaz. Sosyal medya kullanıcıları arasındaki bağlantıları, proteinler arası etkileşimleri ya da internetin yapısı gibi birçok sistemi, çizge kuramı aracılığıyla modellemek mümkündür.
Bu durumda sorunun yeni hali şudur: Bir çizgede, her kenarı yalnızca bir kez geçecek bir yol var mı? Bu sorunun yanıtı düşündüğünüzden daha basittir.
Yapılması gereken, her düğümden çıkan kenarların sayısını incelemektir. Eğer tüm düğümlerden çıkan kenar sayısı çiftse ya da sadece iki düğümden çıkan kenar sayısı tekse, bu tür bir yol mümkündür. Aksi durumda, yani üç ya da daha fazla düğümde kenar sayısı tekse, böyle bir yol çizilemez.
Königsberg Köprüsü Problemi Çözümü Nedir?
Bu sonucun mantığını birlikte inceleyebiliriz. Her kenarı yalnızca bir kez geçen bir yol düşündüğümüzde, bu yol üzerindeki her düğüm—yani köprülerin bağlandığı kara parçası—eğer yolun başlangıcı ya da bitişi değilse, her geldiğinde başka bir kenardan çıkmak zorundadır. Başka bir ifadeyle, düğüme yapılan her girişin, bir çıkışla eşleşmesi gerekir. Bu da, ortada yer alan düğümlerde mutlaka çift sayıda kenar bulunması gerektiği anlamına gelir.
Sadece yolun başladığı ve bittiği düğümler bu kuralın dışında kalır. Bu yüzden, eğer yalnızca iki düğüm tek sayıda kenara sahipse, böyle bir yol mümkündür ve bu yol tam olarak bu iki düğüm arasında gerçekleşir. Eğer tüm düğümler çift sayıda kenara sahipse, yol başladığı düğümde sona erer ve tam bir döngü oluşturur.
Bu açıklama, çizge kuramında kabul edilen ilk temel sonuçtur. Her kenarı yalnızca bir kez geçen bu tür yollara, günümüzde “Euler Yolu” denir. Euler’in sunduğu argüman, bir Euler Yolu’nun neden var olamayacağını açıklayan koşulları ortaya koyar. Kesin matematiksel kanıt ise daha sonra yapılmıştır.
Königsberg köprüleri problemind, dört kara parçasının her birinden tek sayıda köprü çıktığını görürüz. Bu da, orada yaşayanların bu rotayı boşuna aradıkları anlamına gelir. Böyle bir yol yoktur.
Burada dikkat çekici bir yan bilgi var. Eğer amacımız her köprüyü değil de, her kara parçasını yalnızca bir kez ziyaret etmek olsaydı—yani her düğümden sadece bir kez geçmeyi hedefleseydik—karşımıza bambaşka bir problem çıkardı.
İlk bakışta bu durum, Euler Yolu’na benzer. Ancak temelde çok farklıdır ve çözümü çok daha zordur. Bu tür yol arayışına “Hamilton Yolu” denir. Burada amaç, çizgedeki her düğümü bir kez ziyaret ederek bir yol oluşturabilmektir.
Hamilton Yolu probleminin zorluğu, genel olarak çözüm üretmenin sistematik ve hızlı bir yolunun bilinmemesinden kaynaklanır. Bu nedenle, bilgisayar biliminde “zor” kabul edilen problem sınıflarından birine aittir.
Königsberg’in Yedi Köprüsü Yeni Matematiği Nasıl Doğurdu?
Euler, bu köprü problemine ilk etapta pek değer vermedi. Ancak alıştığı matematiksel yöntemlerle çözemeyince ilgisi giderek arttı. Bir arkadaşına yazdığı mektupta şunları söyledi. “Bu soru çok sıradan görünüyordu ama dikkatimi çekti. Ne geometri, ne cebir, ne de sayma sanatı bu sorunu çözmeye yetiyordu.”
Bu fark, Euler’i farklı düşünmeye zorladı. Karşısındaki problem, yeni bir soyutlama biçimi gerektiriyordu. Ve işte bu fark, matematikte köklü bir dönüşümün başlangıcı oldu.
Königsberg haritasını sadeleştirip yalnızca bağlantıları gösteren bir çizgeye indirgeme fikri, bugün bize oldukça açık ve basit görünecektir. Ancak tarihteki en güçlü soyutlamaların birçoğu, geriye dönüp bakıldığında “zaten öyleymiş” hissi verir. Bu, soyut düşünmenin doğasında vardır. Matematiğin tarihi, tam da bu tür düşünce sıçramalarının tarihidir.
Euler’in yayımladığı makale, yalnızca çizge kuramını başlatmakla kalmadı. Aynı zamanda topoloji adını verdiğimiz başka bir temel matematik alanının da öncüsü oldu. Topoloji, şekilleri esnek bir madde gibi düşünerek, onları bükseniz, gerip uzatsanız bile değişmeyen özelliklerle ilgilenir. Bu yaklaşım, ölçülebilir niceliklerden çok, yapısal ilişkileri ön plana çıkarır.
Topolojiye göre, küre, küp ve piramit aynı türdedir; çünkü yeterince esnek kabul edildiklerinde birbirlerine dönüşebilirler. Örneğin bir küpün köşeleri yuvarlatılıp yüzeyleri şişirilerek bir küre formuna getirmek mümkündür. Bu dönüşüm sırasında kopma, yırtılma ya da yapısal bir delik oluşmaz. Bu nedenle, topolojik bakış açısından bu şekiller aynı sınıfta yer alır.
Ancak bir simit—ya da matematikteki adıyla torus—bu sınıfa girmez. Simidin ortasındaki delik, onun ayırt edici özelliğidir ve topolojik olarak korunması gerekir. Yani simidi ne kadar esnetir ya da bükerseniz bükün, o delik yok edilemez; dolayısıyla simit küreye dönüşemez.
Sonuç olarak
Euler’in köprü problemiyle attığı adım, yalnızca yerel bir sorunu çözmekle kalmadı; uzun vadede, geometrinin ne anlama geldiğini sorgulatan bambaşka bir matematiksel düşünme biçiminin de temelini attı. Çizge kuramı ve topoloji, bugün hâlâ matematikte yeni bakış açıları sunmaya devam ediyor. Ve bunu, yüzyıllar önce bir şehirdeki köprüleri adımlayan meraklı insanlara borçluyuz.
Kaynaklar ve ileri okumalar:
- The bridges of Königsberg. yayınlanma tarihi: 5 Ağustos 2016; Bağlantı: The bridges of Königsberg
- How the Seven Bridges of Königsberg Spawned New Math. Yayınlanma tarihi: 9 Mart 2024. Kaynak site: Scientific American. Bağlantı: How the Seven Bridges of Königsberg Spawned New Math
Matematiksel