Günlük yaşamımızda genellikle matematiğin işe yaramayacağını düşünürüz, oysa ki matematik bizimle birlikte doğar. Bizi şifreleyen DNA’mızda, bizim kim olduğumuzu ele veren parmak izimizde ve hatta Facebook’taki arkadaş sayımızda bile matematik vardır.
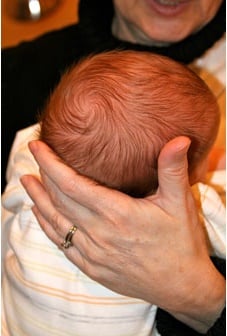
“Matematik bizimle birlikte doğar,” iddiası asılsız değildir. Çocukların sayı saymayı el ve hatta bazen ayak parmaklarıyla öğrenmeye başladığını hepimiz biliyoruz. Parmaklarımız tıpta digit (digitus) olarak bilinir. Aynı kelimenin 10’luk sayma sisteminde 0’dan 9’a kadar olan sayıların her birini temsil etmesi basit bir tesadüften ibaret değildir. Vücudumuz bizim ilk aritmetik öğretmenimizdir. Bedenimiz ayrıca, ona izin verdiğimiz ve işaretleri doğru okuyup, yorumladığımız sürece, bizlere matematik öğretmeye çalışır. Şimdi gelin, yeni doğmuş bir bebeğin saçlarına bakalım.
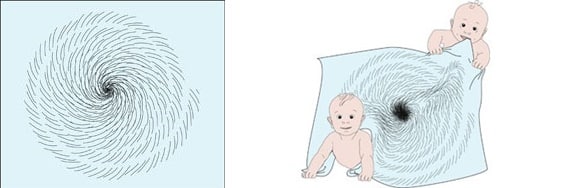
Bu, tatlı küçük kafanın tepesindeki saç kümesi, bebeğin saç tellerinin nereye doğru uzayacağını bilemediği bir karmaşıklık noktasıdır. Bu saç kümesinin arka tarafındaki saçlar sola, ön tarafındaki saçlar sağa, yanlardaki saçlar ise canları nereye isterse oraya doğru uzar. Bu durumun aynısını doğada da gözlemleyebiliriz. Bir kasırga hayal edelim. Kasırganın odağındaki rüzgar, herhangi bir yöne esmez, fakat odaktaki rüzgara yakın rüzgarlar her yöne eser.
Saç tellerinin yönleri, rüzgar hareketleri arasında uyumsuzluk söz konusu olduğunda, bu uyumsuzlukları gidermek için doğanın bulduğu çözüm, onları olabilecek en küçük noktaya hapsetmek olmuştur. Büyüdükçe kafa tasınız ve kafa deriniz de sizinle birlikte büyür. Fakat kafanızın tepesindeki o saç döneği asla kaybolmaz.
Topolojik Kurallar Hepimiz İçin Geçerlidir!
Topoloji, şekillerin sürekli deformasyondan (bozulmadan) sonra bile aynı kalan özellikleriyle ilgilenen bilim dalı olarak tanımlanır. Bebeğimizin saçlarının ince bir elastik kumaş üzerine resmedildiğini hayal edelim. Şimdi bu kumaşın şeklini bozalım, onu uzatalım, bükelim, döndürelim. Fakat asla kesmeyelim veya bir parçasını başka bir parçasına tutturmayalım. Bu gayretimiz, kumaşa resmettiğimiz çizimin geometrik yapısını bozacaktır, fakat çizimin topolojik yapısı aynı kalacaktır. Daha fazlası için: Yeni Başlayanlar İçin Topoloji: Nedir Ve Neden Önemlidir?
Avuç İçi ve Parmak İzlerindeki Desenler de Topoloji İle İlişkilidir
Saç tellerimizi rahat bırakıp, parmak uçlarımıza veya avuç içlerimize daha yakından bakmaya ne dersiniz? Tüm o düzgünce sıralı çizgileri görüyorsunuz değil mi? Bu çizgilerin bazıları komşularıyla paralel paralel yaşamak isterken, bazıları da mahalleye yeni gelenlerle kaynaşmak ister. ( Parmak İzi Nasıl Oluşur Ve Ne İşe Yararlar?)
Çizgiler arasındaki bu çatışma hali, kaçınılmaz süreksizlikler (tekillikler) yaratır. Bunlar sadece el falı bakanların ya da polisin ilgi alanına girmez, girmemelidir. Eğer işaretleri doğru okursak, bu çatışmaların bize, bedenimizin bir topoloji dersi verme çabası olduğunu anlayabiliriz.
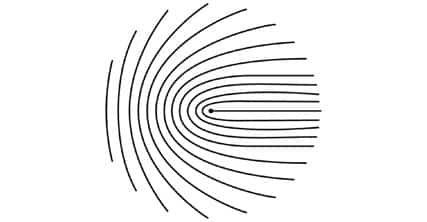
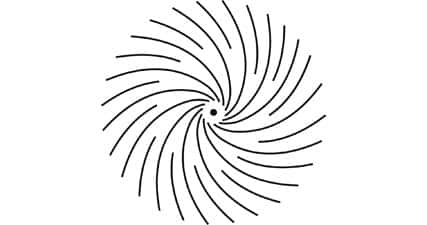
Parmak uçlarımıza baktığımızda, sadece birkaç değişik türde tekillik olduğunu fark edebiliriz. Bunlardan en çok bilinen iki tanesi triradius (üçyarıçap) ve ilmektir.
Diğer tüm tekillikler bu ikisinden elde edilebilir. Örneğin, düğüm olarak bilinen tekillik çeşidi
iki ilmeğin birleşimine karşılık gelir:
Hepimizin Parmak İzi Aynı Matematiksel Kurala Göre Oluşur
1965’te, İngiliz medikal genetikçi Lionel Penrose, parmak ve avuç içi izlerinin evrensel bir kurala uyduğunu göstermiştir. Bu kurala göre, beş parmağa sahip olan herkes, ilmeklerden dört fazla sayıda triradius-a sahip!
Burada şöyle inanılmaz bir ironi var. Parmak ve avuç içlerimiz her ne kadar; bizim, birbirimizden ayırt edilmemize olanak sağlayan belirginliklerimiz olarak anılsa da, bu izlerin geometrileri arasındaki fark o kadar da belirgin değil. Yani aynı topolojik kural hepimiz için geçerli!
Penrose, bulduğu bu kuralı, bazı genetik anormalliklerden dolayı beş parmaktan farklı sayıda parmakla doğan insanları da kapsayacak biçimde genelleştirdi. Sonucunda da ortaya şöyle bir formül çıktı: T-L=D-1. Burada, D her eldeki parmak sayısını, T eldeki triradiusların ve L de ilmeklerin sayılarını belirtiyor. Penrose’un kuralına göre, bir eldeki triradiuslarla, ilmekler arasındaki fark, eldeki parmak sayısından bir eksik.
1979’da Penrose’un, bir matematiksel fizikçi olan oğlu Roger, babasına ithaf ettiği ilgi çekici makalesinde, babasının bulduğu bu kuralın topolojik olarak da doğru olduğunu kanıtladı. Kanıt için: Penrose, R. 1979. “The Topology of Ridge Systems.” Annals of Human Genetics 42 (4): 435–444. doi:10.1111/j.1469-1809.1979.tb00677.x. It can be downloaded from http://onlinelibrary.wiley.com/doi/10.1111/j.1469-1809.1979.tb00677.x/pdf
Kaynak: Singular Sensations. Yayınlanma tarihi: 10 Eylül 2012; Bağlantı: https://archive.nytimes.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel