Veda matematiği (vedic mathematics) ya da Vedik matematik adına internette dönen kısa videolar aracılığı ile denk gelmiş olabilirsiniz. Pratik bazı hesaplama tekniklerinin aktarıldığı bu videoların arka planındaki fikri ve kökenini merak ediyorsanız kısaca aktarmaya çalışalım.

Vedik matematiğin MÖ 1000 civarında ilk olarak Hindistan’ın Yukarı İndus Vadisinde kullanılmaya başlanan matematiksel bir sistem olduğu kabul edilmektedir. Basitçe ifade etmek gerekirse matematiksel işlemleri zihinden hızlı bir şekilde yapılmasını sağlayan, 16 tane temel formülden oluşan yöntemler bütünüdür. Ancak bu sistemin popülerleşmesi 1900’lerin başında Sri Bharati Krsna Tirthaji’nin yoğun çabaları ( 1884-1960) sonucunda olmuştur.
Tirthaji Hindistan’da saygın din adamlarından birisiydi. İlgi alanları arasında Sanskritçe, felsefe, İngilizce, matematik, tarih yer almaktaydı. 1930-1940’lı yıllarda hem dini rehberlik hem de Vedik matematik hakkında vaazlar vererek Hindistan’ı turladı. 1965’te Vedic Mathematics başlıklı bir kitap yayınladı. Bu kitaptaki fikirler de zamanla tüm dünyada kabul görmeye başladı.

Vedik Matematik Nedir?
Vedik matematik, matematiksel hesaplamaları hızlı ve doğru bir şekilde çözmek için bir sutralar veya yöntemler topluluğudur. 16 sutra (Formüller) ve 13 alt sutrası (Alt Formüller) içerir. Bu sutralar ve alt sutralar çeşitli problemlerin çözümünde kullanılmaktadır.
Günümüzde Vedik matematik ile ilgili bahsedilen yöntemlerin çoğu tartışmalıdır. Ancak yine de nasıl yapıldığını basit bir kaç örnek ile açıklamaya çalışalım. Bunun için bir çarpma işleminin nasıl yapıldığını inceleyelim.
Diyelim ki 9 ile 8 sayılarını çarpmak istiyoruz. İlk olarak 9 sayısının 10 sayısından farkı olan 1’i ve 8 sayısının 10 sayısından olan farkı 2’yi alt alta yazmak gerekiyor. Çarpma işlemi iki farklı türlü yapılabiliyor. Şimdi ilk sütundaki rakamları toplayın ve sonuçtan 10 çıkartın. Ya da ikinci sütundaki rakamları toplayın ve sonuçtan yine 10 çıkartın. Yada çaprazlama da toplayabilirsiniz. Her durumda cevap daima yedidir.
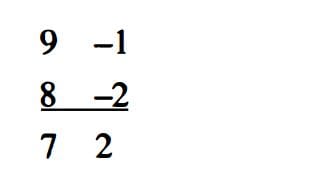
Cevabın ikinci basamağı için de ikinci sütundaki iki sayı çarpmak gerekiyor. Sonuç olarak cevap 72’dir. Bu metot çarpım tablosunu ezberlemede zorlananlar için avantajlı gibi gözüküyor. Ancak aslında bu teknik uzun süredir kullanılmaktadır. Yani aslında sadece Vedik matematik ile ilgili değildir.
İki Basamaklı Sayıların Çarpılması
İki basamaklı sayıların çarpımında da benzer biçimde olur. Bu sefer her sayının 100’den farkı hesaplanmalıdır. Sonra da yanına yazılmalıdır. Önceki çarpma örneğindeki 4 seçenekten en kolay olanı tercih edilerek ilk basamak hesaplanır. ( Bu durumda çapraz toplama). Sağdaki sütundaki sayılar ise normal biçimde çarpılacaktır.

Daha çok basamaklı sayıları çarpmak için benzer bir metotla ancak daha fazla çapraz çarpım yaparak sonuca ulaşmak gerekir. Bu çarpma yöntemi sürece değil sonuca odakladır. Neden sonuç ilişkisini desteklemez ve sayılar büyüdükçe uygulanması zorlaşır.
Tirthaji’nin çabalarının nedeni aslında kolayca anlaşılır. Sonuçta Hindistan kadim bir tarihe sahip olmasına rağmen uzun yıllar İngiliz sömürgesi olarak varlığını sürdürmüştü. Vedik matematik kaybettiği itibarını geri kazandırmak ve dünyaya adını duyurmak için iyi bir seçenek olabilirdi.
Günümüzde ise, fazla bir anlam yüklemediğimiz sürece Vedik matematik sayılar ile oynamanın ve bazı kestirme yolları keşfetmenin eğlenceli bir yolu olarak kullanılabilir. Ancak hepsi bu kadar. Ortada farklı bir matematik söz konusu değildir. Yazının devamında ayrıca göz atmak isterseniz: Çarpım Tablosunu Ezberlemek Zor Değildir, Bilmeniz Gereken Bazı İpuçları
Kaynaklar ve İleri okumalar:
- The Fraud of Vedic Maths; Yayınlanma tarihi: 12 Ağustos 2010; Bağlantı: http://www.openthemagazine.com/
- Explained: What Is Vedic Maths And Does It Originate From Vedas. Yayınlanma tarihi: 2 Mayıs 2022; Bağlantı: https://www.indiatimes.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel