Noether teoremi enerjinin, momentumun ve elektrik yükünün korunumu gibi korunum yasalarını simetrilerle ilişkilendirir.

İnsanlar tarihin eski zamanlarından beri simetriden etkilenmiştir. Sonucunda simetrik cisimler mükemmelliği, dengeyi ve düzeni anlatan şekillerdir. Simetri, her zaman olabildiğince basit olmayı amaçlayan, evrenin zarif bir açıklaması gibidir.
Aslına bakarsanız pek çok fizik yasasının gelişimi de simetri kavramına dayanır. Simetri dediğimiz zaman aklımıza hemen geometri gelse de fizikte simetri farklı bir anlam taşır. Örneğin, bir deneyi ister bugün ister önümüzdeki hafta yapın, her şeyin aynı olması koşuluyla aynı sonucu alırsınız. Fizik açısından ele aldığımız da bu da bir simetridir.
Bu, zaman-öteleme simetrisi, fizikteki en ünlü yasalardan birini ortaya çıkarır. Bu enerjinin sıfırdan yaratılıp yok edilemeyeceğini, ancak bir biçimden diğerine dönüşebileceğini söyleyen enerjinin korunumu yasasıdır. Aşağıdaki fizikte simetri dendiğinde neler düşünmemiz gerektiği konusunda kısaca bir fikir verecektir.

Korunum Yasaları Ve Simetri Arasındaki İlişki Nedir?
Enerji ve momentumun korunumu gibi korunum yasaları kuramsal fiziğin önemli bir parçasıdır. Bir sistemin zaman içindeki davranışlarını tahmin etmek için sıklıkla korunum yasalarından yararlanılır. Önce toplam korunum yasalarını ifade eden çeşitli denklemler yazılır. Daha sonra da zaman içinde meydana gelecek değişimleri tahmin etmek için bu denklemlerden yararlanılır.
Fizikte korunum terimi, değişmeyen bir şeyi belirtir. Bu, bir denklemde, korunan bir niceliği temsil eden değişkenin zaman içerisinde sabit olduğu anlamını taşır. Bu değişken, olayın öncesinde ve sonrasında aynı değeri taşır.
Korunum yasaları, doğada hangi süreçlerin meydana gelip gelemeyeceğini tanımlamaları açısından doğa ve evreni anlamanın temelini oluşturur. Bu yasaları kullanarak kullanarak korunumlu nicelikleri ve hareketi tanımlayabiliriz. Sistemin özelliklerini diğer çözüm türlerinden çok daha hızlı hesaplayabiliriz. Doğa kanunları nerede olduğunuza, hangi yönde hareket ettiğinize veya saatin kaç olduğuna bağlı değildir.

Fizikte simetri ve korunum yasaları dediğimizde de akla gelmesi gereken isim Emmy Noether olacaktır. Korunum yasaları fiziğin bir dizi farklı alanında yararlıdır, ancak bazen çok karmaşık hale gelebilirler. Noether tarafından 1910’larda geliştirilen bir teoremin işe yaradığı yer burasıdır. Emmy Noether’in teoremi, simetri ve korunum yasalarını birbirine bağlar.
Amalie Emmy Noether, çalışmalarında özellikle cebire odaklanan bir matematikçiydi. Çalışmaları, fizikte matematiksel yöntemlerin geliştirilmesiyle ilgilenen matematiksel fizik adlı bir dalda da son derece etkiliydi. Kendisi hem saf hem de uygulamalı matematiğe temel katkılar sağladı. En önemli başarısı Noether teoremi olarak kabul edilmektedir.
Klasik Fizikte Korunum Yasaları Nedir?
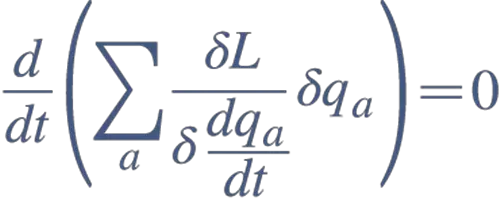
Noether teoremi enerjinin, momentumun ve elektrik yükünün korunumu gibi korunum yasalarını simetrilerle ilişkilendirir. Her simetriye karşılık gelen bir korunum yasası ve her korunum yasasına karşılık gelen bir simetri olduğunu söyler. Kısacası bir sistemde hangi niceliklerin zaman içinde değişmediğini merak ediyorsanız sistemin hangi simetrilere sahip olduğuna bakmanız gerekir.
Noether’in teoremi günlük hayatta aşina olduğumuz simetriler ile ilgili değildir. Bir kare dönel simetriye sahiptir. 90 derecelik (veya 180, 270 derecelik) bir dönme sonrasındaki görünümü, dönme öncesiyle aynıdır. Bu tarz bir simetriye kesikli ya da süreksiz simetri denir. Daha önceki koşullarına dönmek için sonlu değişiklikler yeterli olur.
Ancak fizikte bir de sürekli simetriler vardır. Sürekli simetriler fiziksel bir sistemin sonsuz küçük ve sürekli dönüşümler altında her yerde aynı davrandığı simetri türüdür. Noether teoremi sürekli bir simetridir.
Noether Teoremi Ne Anlama Gelir?
Çok sayıda parçacıktan oluşan bir sistem olduğunu düşünelim. Parçacıkların zaman içindeki davranışlarını tahmin etmek istiyorsanız, ilk olarak koordinatlarını tespit etmeniz gerekecektir. Bunun için de bir koordinat sistemi tanımlamanız gereklidir.
Ancak bu koordinat sistemini tanımlama biçiminiz keyfidir. Tanımladığınız koordinat sistemini, belirli bir yönde ötelemeniz durumunda yapacağınız tahminlerde herhangi bir fiziksel değişikliğe sebep olmaz. Örneğin ilk koordinat sistemindeki hesaplarda bir parçacık giderek hızlanıyorsa ikinci koordinat sistemindeki hesaplarda da aynı biçimde hızlanacaktır.
Sonucunda değişen sadece koordinatlardır, fiziksel süreçler değildir. Uygulanan öteleme işlemi herhangi bir fiziksel değişime sebep olmadığı için sistemde ötelenme simetrisi olduğu söylenir. Noether teoremi, bu sürekli simetriye karşılık gelen bir korunum yasası olduğunu söyler.
Hesaplar yapıldığında zaman içinde değişmeyen niceliğin parçacıkların toplam doğrusal momentumu olduğu görülür. Bu nedenle de doğrusal momentumun korunumu ile ötelenme simetrisi arasında bire bir ilişki vardır. Şimdi de koordinat sitemini bir eksen etrafında döndürdüğümüzü düşünelim. Bu durumda da fiziksel süreçlerde bir değişiklik olmayacaktır. Noether’in teoremi bu dönme simetrisine karşılık gelen bir korunum yasası olduğunu söyler.
Hesaplar yapıldığında da bu sefer zaman içinde değişmeyen niceliğin sistemin toplam açısal momentumu olduğu görülür. Dönme simetrisi ile açısal momentumun korunumu arasında bire bir ilişki vardır.
Noether Teoremi Günümüzde Ne İşe Yarar?
Noether’in ünlü teoreminin açıklandığı 23 Temmuz 1918’den bu yana bir asırdan fazla zaman geçti. Ancak önemi günümüzde de devam etmektedir. 20. yüzyılın ikinci yarısında, Noether teoremi, doğayı küçük ölçeklerde tanımlayan ve 2012’de keşfedilen bir parçacık olan Higgs bozonunun varlığını tahmin eden standart parçacık fiziği modelinin temeli haline geldi.
Bugün fizikçiler hala Noether’in çalışmasına dayanan yeni teoriler formüle ediyorlar. Noether teoremleri, iki farklı teoriyi yani genel görelilik ve kuantum mekaniğini birleştirecek potansiyel kuantum yerçekimi teorileri geliştirmek için temel araçtır. Noether’in çalışması, bilim insanlarının böyle birleşik bir teoride ne tür simetrilerin ortaya çıkabileceğini anlamalarına yardımcı oluyor.
Kaynaklar ve ileri okumalar:
- In her short life, mathematician Emmy Noether changed the face of physics. Yayınlanma tarihi: 12 Haziran 2018; Bağlantı: https://www.sciencenews.org/
- Symmetry and Symmetry Breaking; https://plato.stanford.edu/entries/symmetry-breaking/
- Symmetry and Conservation Laws; https://www.feynmanlectures.caltech.edu/III_17.html
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel