“Bir fizik kuramı, matematiksel güzelliğe sahip olmalıdır.” Paul Dirac’ın 1956’da fiziğin özüne ilişkin görüşünü ifade etmesi istendiğinde verdiği yanıt buydu. Bu yanıtın devamında da fiziğin tüm denklemleri arasında belki de en güzel olan Dirac denklemini formüle edecekti.
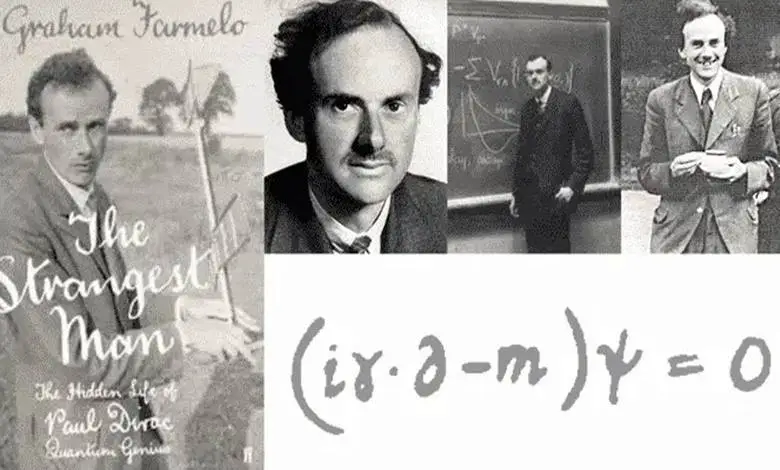
İngiliz teorik fizikçi Paul Dirac, kuantum fiziğinin ilk günlerinin en önemli isimlerinden biriydi. Bunun sonucunda da Erwin Schrödinger ile birlikte 1933’te Nobel Fizik Ödülü’nü kazandı. Dirac’ın 1930’da, 27 gibi oldukça genç bir yaşta Royal Society’ye üye seçilmesi, onun bilimsel saygınlığının bir göstergesi idi.
İleri matematiğe olan tutkusuna karşın, Dirac basit olan ve fizik problemlerinin çözümünde doğrudan kullanılabilen matematik kavramları yeğlerdi. Ona göre doğa yasalarının belirleyici niteliği, yüksek düzeyde matematiksel “güzellik”ti. Güzel matematik denklemleriyle fiziksel dünyanın işleyişi arasında derin bir uyum vardı.
Paul Dirac Ve Anti Maddenin Keşfi

20. yüzyılın ilk çeyreği fiziğin altın dönemlerinden biri idi. Neredeyse her gün birisi evren anlayışımızda devrim yaratan yeni bir teori ortaya çıkıyordu. 1905’te Einstein, fizikçilerin uzay ve zaman hakkındaki düşüncelerini değiştiren Özel Görelilik Teorisini yayınladı. On yıl sonra da devrim niteliğinde olan Genel Görelilik Kuramı’nı yayınlayacaktı.
Bu sırada da bir grup fizikçi elektronlar ve bu küçük parçacıkların ışık ile olan etkileşimleri ile ilgili çalışmalar yapıyordu. Bu çalışmalar kuantum fiziğinin temellerini atıyordu. Bu dönemde bir çok fizikçi görelilik ile kuantum fiziğini birleştirmeye çalıştı. Ancak bu fizikçileri bekleyen bir de sorun vardı.
Göreliliğin temel fikirlerinden biri, zaman ve uzayın göreceli olduğu ve her şeyin nerede olduğunuza ve ne kadar hızlı hareket ettiğinize bağlı olduğudur. Ancak bu fikir kuantum mekaniğinin hiçbir yerinde ortaya çıkmıyordu. Sonunda Paul Dirac, Einstein’ın ünlü E=mc2 denklemini Schroedinger’in denklemiyle birleştirerek bu sorunu çözmeye karar verdi.
Dirac denklemi nedir?
1928’de Dirac, şu anda Dirac Denklemi dediğimiz şeyi yayınladığı bir makale yazdı. Bu denklem, bir elektronun ışık hızına yakın bir hızda hareket ederken davranışını tanımlamaktadır. Bu, bir elektron için Schrödinger dalga denkleminin göreli bir biçimidir.

Ancak elde ettiği şey bir karmaşa gibi gözüküyordu. Dirac’ın denklemi elektrona benzeyen fakat onun aksine pozitif elektrik yükü taşıyan bir parçacığın da hareketini göstermişti. Dirac buna antielektron adını verdi. Matematiğin işe yaraması için negatif enerjiye sahip fazladan bir tür elektron eklemesi gerektiğini fark etti.
Kimse bunun ne olduğunu, hatta ne anlama geldiğini o dönemde bilmiyordu. Ama sonuç o kadar basit ve zarifti ki Dirac bunun doğru olduğunu biliyordu.1927’den önce kimsenin böyle bir “antimadde” dünyasının var olabileceğine dair en ufak bir fikri yoktu. Ancak Dirac bu fikri tamamen değiştirdi.
Günümüzde yüklü her temel parçacığın kendi antiparçacığı olduğunu biliyoruz. Bu anti-parçacıklar kelimenin tam anlamıyla normal maddenin ayna görüntüleridir. Her anti-parçacık, kendisine karşılık gelen parçacıkla aynı kütleye sahiptir, ancak elektrik yükleri terstir. Bir parçacık, antiparçacık ikiziyle karşılaştığında, iki parça da ortadan kaybolur. Sonrasında da kütleleri, foton veya gluon gibi yüksek enerjili parçacıklara dönüşür.
Sonuç Olarak;

Sadece birkaç yıl sonra, üst atmosferdeki kozmik ışın gözlemleri, Dirac’ın hipotezini doğrulayan ilk antimadde parçacıklarını keşfetti. Bu keşif aynı zamanda görelilik ve kuantum mekaniğinin birleştirilebileceğini ve tamamen yeni bir fizik dalı yaratılabileceğini gösterdi. Bu kuantum alan teorisi idi.
Westminster Abbey ya da resmi adı ile Westminster’deki Aziz Peter Kilisesi, Londra’nın Westminster kentinde yer alan önemli bir kilisedir. Bu kilisenin zeminine yazılmış iki denklemden biri Dirac denklemidir. Diğeri ise Stephen Hawking’in kara deliklere ilişkin denklemidir.

“Fiziğin tüm denklemleri arasında belki de en büyülü olanı Dirac denklemidir”; diyor Amerikalı fizikçi Frank Wilczek. Bu da bize Paul Dirac’ın hayatı boyunca peşinden koştuğu matematiksel güzelliği elde ettiğini kanıtlıyor.
Kaynaklar ve ileri okumalar
- How Dirac predicted antimatter. Yayınlanma tarihi: 12 Mayıs 2009. Kaynak site: New Scientist. Bağlantı: How Dirac predicted antimatter
- In 1928, One Physicist Accidentally Predicted Antimatter. Yayınlanma tarihi: 23 Temmuz 2017. Kaynak site: Popular Science. Bağlantı: In 1928, One Physicist Accidentally Predicted Antimatter
- ‘The most magical equation in physics’. How Paul Dirac accidentally revealed the strange world of antimatter. Yayınlanma tarihi: 5 Ağustos 2023. Kaynak site: LİveScience. Bağlantı: ‘The most magical equation in physics’. How Paul Dirac accidentally revealed the strange world of antimatter
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel