Henüz Çözülememiş 11 Matematik Problemi İle Tanışın

Matematikte hâlâ çözülememiş pek çok problem vardır. Özellikle sayıların yapısını inceleyen sayı teorisinde, konuya nereden bakarsanız bakın, derine indikçe karşınıza mutlaka çözülmemiş bir problem çıkar. Bu tür problemler, ilk bakışta sanki kolayca çözülebilecekmiş gibi görünür. Ancak ne kadar uğraşırsanız uğraşın, cevaba bir türlü ulaşamazsınız. İşte bazı örnekler…

1- Goldbach Hipotezi

Matematikçileri yıllardır uğraştıran en ünlü varsayımlardan biri, 1742 yılında Alman matematikçi Christian Goldbach’ın İsviçreli matematikçi Leonhard Euler’e yazdığı bir mektupla gündeme geldi. Goldbach, mektubunda, ikiden büyük her tam sayının üç asal sayının toplamı olduğunu öne sürdü. Euler ise bu ifadenin, “2’den büyük her çift sayı iki asal sayının toplamıdır” şeklinde daha sade bir biçimi olduğunu söyledi.

Bugün Goldbach varsayımı olarak bilinen bu önerme, oldukça basit bir soruya dayanır. “İkiden büyük her çift sayı, iki asal sayının toplamı olarak yazılabilir mi?”

Bu soruya kesin bir “evet” ya da “hayır” cevabı verebilmek için matematikçiler uzun yıllardır uğraşıyor. Şimdiye kadar çok büyük sayılar için bilgisayarlar yardımıyla hipotezin doğru olduğu gösterildi. Ancak kimse, bu durumun tüm çift sayılar için geçerli olduğunu kanıtlayabilmiş değil.

2- Riemann Hipotezi

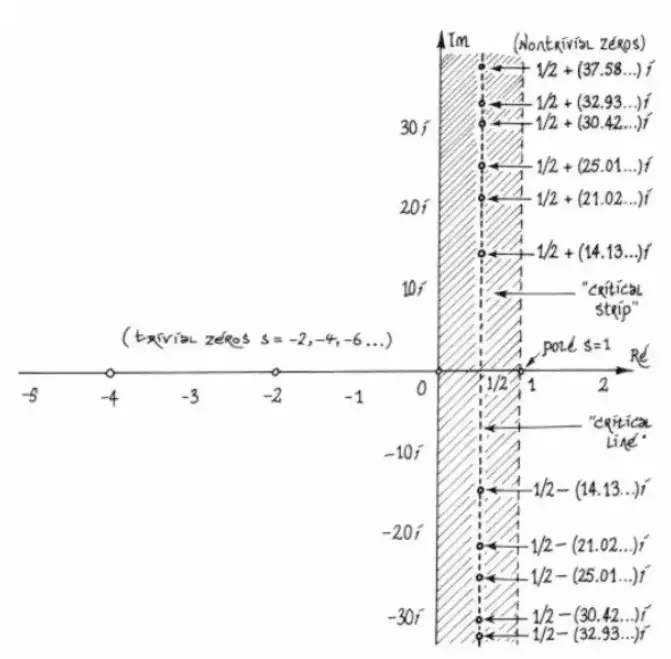
Dünyanın en zor ve en ünlü matematik probleminin hangisi olduğunu kesin olarak söylemek mümkün değil. Ancak Bernhard Riemann’ın 1859 yılında ortaya attığı Riemann Hipotezi, bu unvana aday gösterilebilecek bir problem olarak öne çıkıyor.

Riemann Hipotezi, David Hilbert’in 1900 yılında yayımladığı çözülmemiş 23 problem listesindeki sekizinci sırada yer alır. Aynı zamanda, Clay Matematik Enstitüsü tarafından 2000 yılında belirlenen “Millennium Ödül Problemleri” arasında da en önemli ikinci problem olarak kabul edilir.

Bu hipotez, asal sayıların kendisinden çok, asal sayıların sayı doğrusu üzerindeki dağılımıyla ilgilidir. Riemann Hipotezi’ne verilecek yanıt yalnızca bir “evet” ya da “hayır” olabilir. Ancak bu cevaba ulaşmak için öne sürülen yollar oldukça karmaşıktır ve bugüne kadar hiçbiri kesin çözüme ulaşamamıştır. Eğer ispatı doğru çıkarsa bu, uzun yılların en önemli matematik başarılarından biri olacaktır. Detaylar için: Riemann Hipotezi: Dünyanın En Zor ve Ünlü Problemi

3- İkiz Asal Varsayımı

İkiz asal sayılar varsayımı, sayı teorisinin en dikkat çekici problemlerinden biridir. Söylemesi kolay, ancak kanıtlaması son derece zordur. Bu varsayım, farkı yalnızca 2 olan asal sayı çiftlerinin sonsuz sayıda olduğunu öne sürer. Örneğin (3, 5), (11, 13) ve (29, 31) bu tür çiftlere örnektir.

Matematikçiler, 18. yüzyıldan beri asal sayıların küçük sayılar arasında daha sık, büyük sayılara doğru ise giderek daha seyrek bulunduğunu biliyor. İkiz asal sayılar ise normal asal sayılardan bile daha enderdir. Bu nedenle yeni ikiz asal çiftleri bulmak her zaman kolay olmamıştır. Ancak sayı teorisyenleri, seyrekleşse de, eninde sonunda yeni bir ikiz asal çiftiyle karşılaşacağınızı varsayar.

Bilgisayar destekli hesaplamalar da bu düşünceyi destekliyor. Bugüne kadar bulunan en büyük ikiz asal çifti 388.342 basamak uzunluğunda. Yine de, bilgisayarlar bu çiftlerin sonsuz sayıda olduğunu hiçbir zaman ispatlayamaz. Bunun için çok daha güçlü yöntemler gerekiyor.

4- NP Problemlerinin Gerçekte P Problemleri Olup Olmadığı

“P ile NP eşit midir?” sorusu 21. yüzyılın hayati matematik problemlerinden biridir. Çünkü bilgisayar biliminin en büyük bilinmezi olan bu soruya doğru bir cevap verilirse, sonuçları milyarlarca dolarlık olacaktır. Eğer bu problem çözülürse:

• Bilim devrim geçirir. Protein katlanmalarından hava durumu simülasyonlarına kadar, çok fazla hesaplama gerektiren işler aniden yapılabilir hâle gelir.
• Diğer altı Milenyum Problemi de mekanik olarak çözülecektir. Eğer P = NP ise, bu problemleri çözmek için gereken kanıtları bulmak da algoritmik olarak mümkün olur.
• Mevcut tüm çevrimiçi güvenlik sistemleri çöker. Şifreleme yöntemlerinin çoğu, bazı problemleri çözmenin “zor” olduğuna dayanır. P = NP olursa, bu “zor” problemler bir anda kolaylaşır.

Teorik bilgisayar biliminin bir alt dalı olan karmaşıklık kuramında (complexity theory), araştırmacılar bilgisayarların belirli türdeki problemleri ne kadar kolay çözebildiğini anlamaya çalışır. P, bilgisayarların verimli (yani makul sürede) çözebildiği problemleri temsil eder. NP ise, bilgisayarların bir çözümün doğru olup olmadığını verimli şekilde doğrulayabildiği problem sınıfıdır.

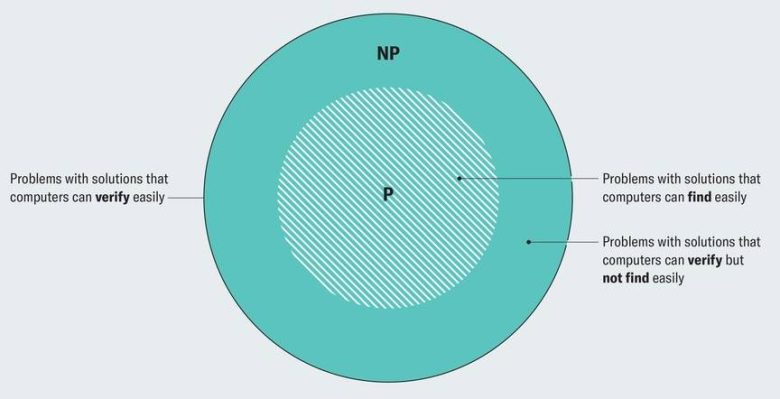
Bu ilişkiyi genelde basit bir Venn diyagramıyla gösteririz: P, NP kümesinin içinde yer alır. Ancak asıl soru şudur. P ve NP gerçekten farklı kümeler mi, yoksa aslında aynı küme mi? İşte bu, P ≠ NP mi yoksa P = NP mi sorusudur — ve bilgisayar biliminin en büyük gizemlerinden biridir.

5- 3n+1 Yani Collatz Problemi

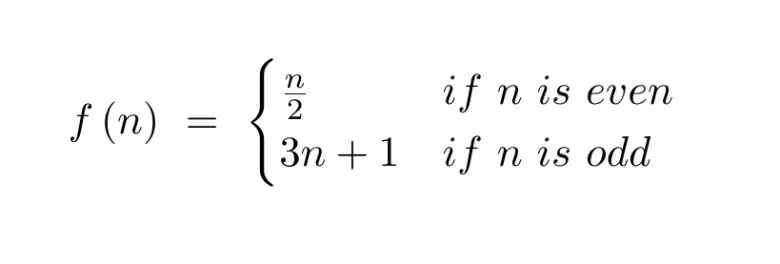
Collatz Problemi, diğer adıyla 3n+1 Problemi, matematikçileri onlarca yıldır meşgul eden çözülmesi zor bir muammadır. İlk bakışta bu problem saçma derecede basit görünecektir. Yine de uzmanlar onlarca yıldır boşuna çözüm arıyor.

Sadece bir sayı seçin, herhangi bir sayı: Eğer çiftse, ikiye bölün; tekse, üçle çarpıp bir ekleyin. Ortaya çıkan yeni sayıyla aynı işlemi tekrar edin. Sonra tekrar. Tekse 3x + 1, çiftse x / 2. Bu işlemleri tekrar tekrar yapın. Collatz sanısına göre, hangi doğal sayıdan başlarsanız başlayın, sonunda mutlaka 1’e ulaşırsınız.

Göreceksiniz ki hangi sayıyla başlarsanız başlayın sayılar eninde sonunda 4, 2, 1, 4 … döngü­süyle devam edecek. Örneğin n=5 için 5, 16, 8, 4, 2, 1, 4, 2, 1 şeklinde olacaktır. Benzer biçimde n=11 için, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1. Aşağıdaki örneklerde diğer sayılar için alacağı sonuçları da görebilirsiniz.

Araştırmacılar Collatz sanısını 2⁶⁸’in altındaki tüm sayılar için test etti. Bu yaklaşık 3 x 10²⁰ farklı başlangıç değeri anlamına geliyor. Bu sayıların tamamı, Collatz sanısını sağlıyor. Yani işlem tekrarlandığında hepsi sonunda 1’e ulaşıyor. Ancak bu, evrende başka bir yerde sanıya uymayan bir sayı olmadığını kanıtlamıyor.

Şimdiye kadarki en büyük ilerleme, 2019 yılında Terence Tao tarafından kaydedildi. Tao, doğal sayıların neredeyse tüm başlangıç değerlerinin eninde sonunda 1’e yakın bir değere ulaştığını ispatladı. Ne yazık ki Tao’nun yöntemi istatistiksel dayanaklara dayandığı için tüm sayılar için genellenemiyor. Diğer tüm yöntemler de çıkmaza girmiş durumda. Bu da Collatz sanısının belki de yanlış olabileceği düşüncesini akla getiriyor.

6- 196 sayısı bir Lychrel sayısı mıdır?

Sayılar ile uğraşmayı seven kişileri eğlendirebilecek, ilginç özelliklere sahip belirli sayı kategorileri vardır. Palindromik sayılar bunlardan biridir. Palindromik sayı, basamakları sağdan sola ve soldan sağa aynı olan bir sayıdır. Örneğin, 383, 12321 ve 9876789 palindromiktir.

Herhangi bir sayıdan bir palindromik sayı üretmek mümkündür. Bunun için tek yapmamız gereken, bir palindroma ulaşana dek sayıya onun tersini (yani, rakamları ters sırada yazılmış sayıyı) eklemektir. Örneğin, 23 sayısından başlanarak bir palindroma bir basamakta ulaşılabilir: 23 + 32 = 55, bir palindromdur.

Eğer 75 sayısından başlanırsa aynı işlemi iki defa yapmanız gerekecektir: 75 + 57 = 132, 132 + 231 = 363. 86’tan başlanırsa aynı biçimde bir palindroma üç adımda ulaşabilirsiniz. 86 + 68 = 154, 154 + 451 = 605, 605 + 506 = 1111. Başlangıç sayısı 97 olduğunda bir palindroma ulaşmak için gerekli basamak sayısı altı; 98 olduğunda ise bu sayı yirmi dörttür.

Aslına bakarsanız 10.000’in altındaki sayıların büyük çoğunluğu 4 veya daha az adımda bir palindrom oluşturur. Ancak 196 sayısını kullanmamaya dikkat edin; çünkü bu sayı, bir palindroma ulaşmak konusunda sizin yeteneklerinizi tamamıyla aşacaktır. Yukarıda anlattığımız biçimde toplama yaptıktan sonra bir palindrom vermeyen sayılara Lychrel sayısı denir. Lychrel terimi, bu konu için çok fazla çaba harcayan bilgisayar bilimcisi Wade Van Landingham tarafından icat edilmiştir.

Lychrel sayısı olmaya aday olan tek sayı 196 değil. Aslında 1000’in altındaki tüm sayıları dikkate alırsak 196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986 da Lychrel sayısı olma adayıdır.

7- Taşınan Kanepe Problemi

Yeni bir eve taşındığımız zaman en büyük sorunlardan bir tanesi, mevcut mobilyaları yeni evin odalarından birine taşımaktır. Sonuçta mobilyalar bir önceki eve göre alındığı için çoğu zaman koridorlardan geçmez. Hele ki koridor düz biçimde değil ise bu daha da büyük bir dert halini alır.

Sonuçta matematikçilerin de sıradan insanlar gibi bir hayatı var. Bir taşınma esnasında akla gelip gelmediği bilinmese de bu konu matematikte daha özelinde geometride bir problemin ortaya çıkmasına neden olmuştur. Bu problem yani taşınan kanepe problemi ( İng: moving sofa problem) hala çözümsüz bekleyen problemler arasında yer almaktadır.

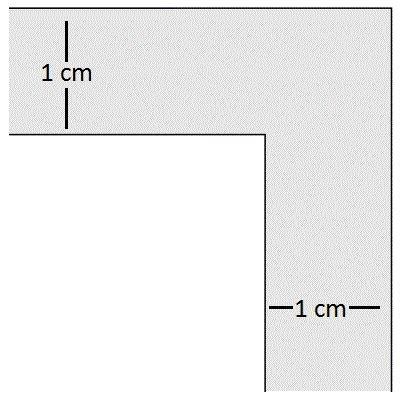
Öncelikle gerçek dünyanın aksine problemi iki boyutlu düşünmeniz gerekiyor. Bu nedenle kanepeyi yukarı kaldırma şansınız yok. Taşınma esnasında yukarıdaki gibi bir koridora denk geldiğinizi düşünelim. Bu tip bir koridordan itekleyerek bir mobilya taşımaya çalıştığınız zaman elbette bazı mobilyalar kolayca L kısmından dönecektir ve bazıları da doğal olarak dönemeyecektir. Peki, bu köşeden dönmesi mümkün olan en büyük koltuğun alanı sizce nedir? İşte taşınan kanepe problemi bu sorunun cevabını arıyor.

8- Mutlu Son Problemi

Bir matematik problemini güzel yapan şeylerden birisi, onu çözmeye çalışırken bazı beklenmedik keşifler yapma potansiyelinizin olmasıdır. En azından Esther Klein’ın 1933’teki deneyimi böyleydi. Üstelik bu keşif beklenmedik bir biçimde mutlu bir sonla bittiği için matematikte önemli bir probleme de adını verecekti.

Bu problem açıklaması oldukça kolay ancak tüm cevaplama girişimlerine meydan okuyan matematiksel problemlerden biridir. Konu oldukça basittir çünkü temelinde bir kağıda çizilen noktalar ve bunları birbirine bağlayarak oluşturabileceğiniz şekillerle ilgilidir.

Bir kağıda çizilmiş, hepsi düz bir çizgi üzerinde yer almayan yani doğrusal olmayan üç noktanız olsun. Bu üç noktayı köşeler olarak kabul ederseniz bir üçgen çizebilirsiniz. Elinizde dört nokta olduğunda da (üç tanesi aynı çizgide olmayan) bunları birleştirerek dört kenarlı bir şekil çizebilirsiniz.

Aslında dört kenarlı şekiller için 5 nokta lazımken, beş kenarlı şekiller için 9, altı kenarlı şekiller içinse 17 nokta gerekir. Peki bir dışbükey yedigen çizebildiğinizden emin olmak için kaç noktaya ihtiyacınız var? Bunu kimse bilmiyor. Detaylar: Anlaması Kolay Çözmesi Zor: Mutlu Son Problemi

9- Alanı ve Köşegeni Tam Sayı Olan Bir Euler Tuğlası Bulma

Varlığı ya da yokluğu matematikçiler tarafından ispat edilmemiş olan bir çözümsüz matematik problemi daha. Problem aslında şunu söyler: bir küboid şekilde (üç boyutlu uzayda) a > b > c iken; hacim köşegeni ve yüzey köşegenlerinin tamsayı olduğu mükemmel küboid bir şekil var mıdır?

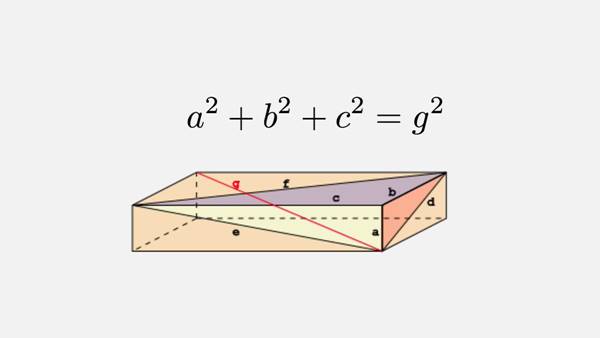
Daha basit anlatalım. Dik üçgenin kenarları arasında kurulan Pisagor teoremini herkes bilir. (3-4-5), (5-12-13) gibi Pisagor üçgenlerinde ise tüm kenar uzunlukları tam sayıdır. Şimdi bu fikri üç boyuta taşıyalım. Üç boyutlu uzayda, dört sayı var.

Yukarıdaki resimde, bunlar a, b, c ve  g olarak gösterilmekte. İlk üçü kutunun boyutları ve g de kutunun bir üst köşesinden alt zıt kösesine giden bir köşegenin uzunluğu. Euler’in tuğlası diye de isimlendirilen bu soruda amaç tuğlanın bütün yüzey köşegenlerinin tamsayı olması (d, e ve f) aynı zamanda hacim köşegenin de tamsayı olmasıdır.(g)

Bu kutu mükemmel kuboid olarak isimlendiriliyor. Matematikçiler birçok olasılığı denediler ve henüz bir tane bile bulamadılar. Fakat böyle bir kutunun olmadığını da ispatlayamadılar, bu nedenle mükemmel kuboid avına devam…  

10- Herhangi Bir Mükemmel Tek Tam Sayı Var mı?

Bir sayının mükemmel olabilmesi için (kendisi hariç) pozitif tam bölenlerinin toplamı bu sayıya eşit olmalıdır. Örneğin 6’nın kendisi hariç pozitif tam bölenleri 1, 2, 3 ‘tür. Bu sayıların toplamı (1+2+3) ise 6’yı verir. Bu nedenle 6 mükemmel bir sayıdır. 28 de 6 gibi mükemmel bir sayıdır. 28’ in kendisi hariç tam bölenleri 1, 2, 4, 7 ve 14 ‘tür. Bu sayıların toplamı da 28 ‘dir.

Mükemmel sayılar hem matematikçileri hem de matematikçi olmayanları tarih boyunca büyülemiştir. Bunun en temel nedeni tanımlanmalarının kolay olmasından gelir. Ancak matematikteki en eski problemlerden birisi de mükemmel sayılar ile ilgilidir.

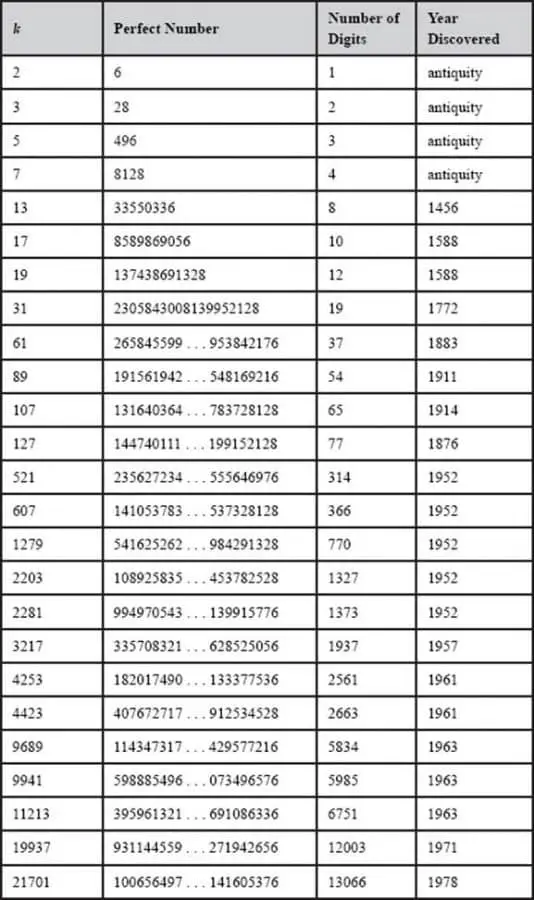
Bugüne kadar 51 mükemmel sayı keşfedildi; en büyüğü 49.724.095 basamaklıdır. Aşağıda mükemmel sayıların bazılarının bir listesini görebilirsiniz. Ancak sizin de dikkatinizi çekeceği gibi bu listedeki tüm sayılar çifttir. İşte bu nedenle de matematikçiler tek mükemmel sayı olup olmadığını yıllardır sorguluyor. 

11- Navier – Stokes Denklemleri

Clay Matematik Enstitüsü‘nün 2000 yılında ortaya koyduğu yedi matematik problemi arasında, içinde yaşadığımız fiziksel dünyaya dair anlayışımızla temel bir şekilde ilgili olan bir problem var. Bu sıvıların akışını tarif eden Navier-Stokes denklemleridir.

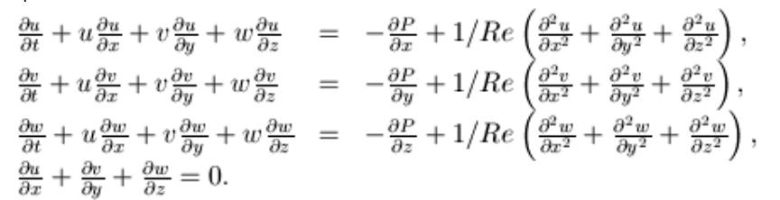
Claude-Louis Navier ve George Gabriel Stokes’un isimli fizikçilerin adını taşıyan Navier-Stokes denklemleri, birleştirilmiş kısmi diferansiyel denklemler kümesidir. Bu denklemler hızdaki değişiklikleri, basınçtaki değişiklikleri ve sıvının viskozitesini ilişkilendirir.

Aslında Clay Enstitüsü’nün ödülü vermek için talep ettiği bilgi ise oldukça basittir. Birincisi denklemlerin çözümlerinin varlığına odaklanır. İkincisi ise bu çözümlerin sınırlı olup olmadığını (sonlu kalıp kalmadığını) sorar.

Uygulamada, fiziksel olarak ilgili ve birçok sıvı akışıyla mükemmel uyum sağlayan birçok çözüm biliyoruz. Ancak bu çözümler, Navier-Stokes denklemlerinin yaklaşık çözümleridir. Her ne kadar (yaklaşık) çözümlerimizin doğru olduğundan oldukça emin olsak da, çözümlerin varlığının resmi bir matematiksel kanıtı eksiktir.

Kaynaklar ve ileri okumalar:

• Kuitché, Rostand. (2023). On the Construction of Some Lychrel Numbers.
• 10 Hard Math Problems That Continue to Stump Even the Brightest Minds. Yayınlanma tarihi: 8 Aralık 2023. Kaynak site: Popular Mechanics. Bağlantı: 10 Hard Math Problems That Continue to Stump Even the Brightest Minds/

Matematiksel