Clay Matematik Enstitüsü‘nün 2000 yılında ortaya koyduğu yedi matematik problemi arasında, içinde yaşadığımız fiziksel dünyaya dair anlayışımızla temel bir şekilde ilgili olan bir problem var. Bu sıvıların akışını tarif eden Navier-Stokes denklemleridir.

Bu ödül sorusunun çözümü, doğada her yerde bulunan akışkanların davranışlarına ilişkin anlayışımız üzerinde derin bir etkiye sahip olacaktır. Hava ve su en tanınabilir akışkanlardır. Nasıl hareket ettikleri ve nasıl davrandıkları bilimin doğuşundan bu yana bilim adamlarını ve matematikçileri büyülemiştir.
Peki Navier-Stokes denklemleri nedir? Neyi tarif ediyorlar? Bu denklemleri, diğer denklemlerden daha zor kılan şey tam olarak nedir? Öncelikle baştan bir kabul ile işe başlayalım.
Navier-Stokes denklemlerini anlamak için ciddi bir matematik eğitimine ve fizik konusunda sağlam bir anlayışa ihtiyacımız var. Bu olmadan, bazı çok basit temellerden faydalanmalı ve genellemeler üzerinden konuşmalıyız. Bu nedenle yazının devamında okuyacaklarınız konu hakkında bir fikir vermek amacına hizmet edecektir.
Türbülans Nedir?

Bu kadar aşina olmamıza rağmen türbülans hakkında en az bilinen fenomenlerden birisidir. Bunun nedeni doğası gereği türbülansı ölçümlemenin zorluğudur. Türbülans bir sıvının ya da gazın hareket halindeki düzensizlik olarak tanımlanır.
Nehir girdaplarında veya yangından yükselen dumanda bulabileceğiniz bir hareket türüdür. Türbülans aynı zamanda borulardan akan sıvıların hareketinde de meydana gelir. Atmosferdeki sıcak ve soğuk havanın türbülanslı karışımı, bazen bir uçakta hissettiğimiz sarsıntılı hareketten de sorumludur.
Türbülanssız akış dediğimiz zaman sakince akan bir dereyi düşünebilirsiniz. Sonuçta bu durumda su derenin her noktası aynı hızla aynı yöne hareket eder. Ancak derenin ortasına bir kaya parçası bırakılırsa, akışın farklı kısımlarında, akış hızı ve yönü farklılaşır. Bunun sonucunda da akış türbülanslı hâle gelir.
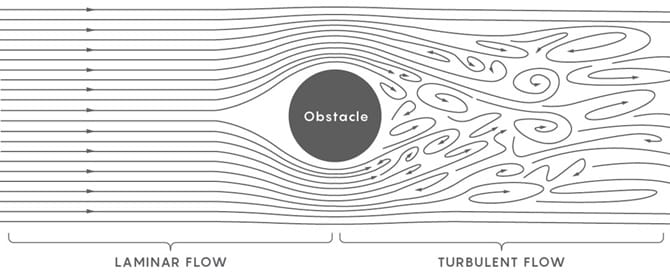
Türbülanslı bir akışta akan suyun hızını ve yönünü ölçerseniz birbirine çok yakın noktalarda çok farklı cevaplar alabilirsiniz. Bu karmaşıklığa rağmen, bilim insanları sıvı akışının Navier-Stokes denklemleri tarafından makul bir doğruluk düzeyinde tanımlandığını kabul eder.
Navier-Stokes Denklemleri Nedir?
Claude-Louis Navier ve George Gabriel Stokes’un isimli fizikçilerin adını taşıyan Navier-Stokes denklemleri, birleştirilmiş kısmi diferansiyel denklemler kümesidir. Bu denklemler hızdaki değişiklikleri, basınçtaki değişiklikleri ve sıvının viskozitesini ilişkilendirir.
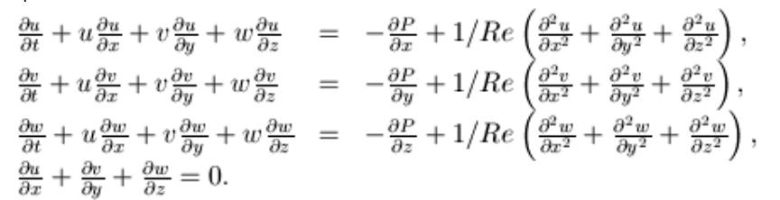
Bir akışkanın hareketini yöneten denklemler, bir akışkan kütlesinin hareketine uygulanan Newton’un İkinci Hareket Yasasının bir ifadesidir. Newton’un İkinci Yasası, akışkan hızının değişim oranlarını akışkana etki eden kuvvetlerle ilişkilendiren bir diferansiyel denklem sistemi üretir.
Türbülanslı akışın zorluğu, denklemlerin arkasındaki matematiği de yansımaktadır. Bir sıvının veya gazın hareketini tanımlamaya çalışırken, peşinde olduğunuz şey, v(x,y,z,t) hızı ve sıvının uzayda (x,y,z) noktasında ve t zamanındaki P(x,y,z,t) basıncıdır. Ancak V ve P fonksiyonlarını bulmak için denklemleri çözmek gerekir.
Aslında Clay Enstitüsü’nün ödülü vermek için talep ettiği bilgi ise oldukça basittir. Birincisi denklemlerin çözümlerinin varlığına odaklanır. İkincisi ise bu çözümlerin sınırlı olup olmadığını (sonlu kalıp kalmadığını) sorar.
Bu Denklemleri Neden Çözemiyoruz?

200 yıldır süregelen deneyler sonucu anladık ki bu denklemler kesinlikle işimize yarıyor. Navier-Stokes’un öngördüğü akışlar, deneylerde gözlemlenen akışlara uyuyor. Ancak sizin de tahmin edebileceğiniz gibi bu denklemleri çözmek çok da kolay değil.
Uygulamada, fiziksel olarak ilgili ve birçok sıvı akışıyla mükemmel uyum sağlayan birçok çözüm biliyoruz. Ancak bu çözümler, Navier-Stokes denklemlerinin yaklaşık çözümleridir. Her ne kadar (yaklaşık) çözümlerimizin doğru olduğundan oldukça emin olsak da, çözümlerin varlığının resmi bir matematiksel kanıtı eksiktir.
Denklemlerin en genel biçimi için kesin matematiksel çözümlerin var olup olmadığını henüz kimse bilmiyor. Ve eğer varlarsa, bir sıvının nasıl davranması gerektiğine dair sezgimizle uyuşmayan süreksizlikler veya sonsuzluklar gibi tuhaflıkları içerip içermediklerini de hala bilmiyoruz.
Akışkanlar mekaniğinin tarihi, Navier-Stokes denklemlerinin tekil çözümler sağlayan basitleştirilmiş versiyonlarının çözümleriyle doludur. Bu gibi durumlarda, yeni bir fiziğin ipucunu vermiştir.
Bu yeni fiziğin tanımlanması araştırmacıların matematiksel modellerini daha da geliştirmelerine ve böylece model ile gerçeklik arasındaki uyumu geliştirmelerine olanak tanıdı. Pek çok kişinin inandığı gibi Navier-Stokes denklemlerinin tekil çözümleri varsa, o zaman belki de bir sonraki Milenyum Ödülü, tekilliği ortadan kaldırmak için hangi yeni fiziğin gerekli olduğunu keşfeden kişiye verilecektir.
Kaynaklar ve İleri Okumalar:
- What Makes the Hardest Equations in Physics So Difficult?. Yayınlanma Tarihi: 16 Ocak 2018; Bağlantı: https://www.quantamagazine.org
- Maths in a minute: The Navier-Stokes equations; Yayınlanma tarihi: 2 Eylül 2015; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





