Günlük hayatımızda etrafımızda gerçekleşen ancak bize sıradan şeyler gibi gelen pek çok fiziksel olay vardır. Bunlardan birisi de çay içerken karşınıza çıkan çay yaprağı paradoksudur.

Şimdi kendinize bir bardak, eski usul demlenmiş ve süzgeçten geçmemiş yani içinde hala çay taneciklerinin bulunduğu bir bardak çay doldurun. Ardından karıştırın. Ne gözlemlediniz? Dikkat ettiyseniz çay tanecikleri karıştırdıktan sonra çayın ortasında kümelendi. Ancak normal koşullarda merkezkaç kuvveti olarak isimlendirilen başka bir fizik yasası nedeniyle bu taneciklerin kenarlarda birikmesi gerekiyordu.
Merkezkaç kuvvetine rağmen nasıl oluyor da yapraklar merkezde toplanıyor? İşte buna
çay yaprağı paradoksu (Tea Leaf Paradox) denmiştir. Adında bir paradoks geçmesi sizi yanıltmasın. Paradokstan ziyade bir fizik problemi ile karşı karşıyayız. Bu problemin çözümüne yönelik ilk doğru tespit 1857 yılında İngiliz fizikçi ve mühendis James Thomson tarafından yapılmış, daha sonra paradoksun asıl çözümü 1926 yılında Albert Einstein tarafından verilmiştir.
Çay Yaprağı Paradoksu Neden Gerçekleşiyor?
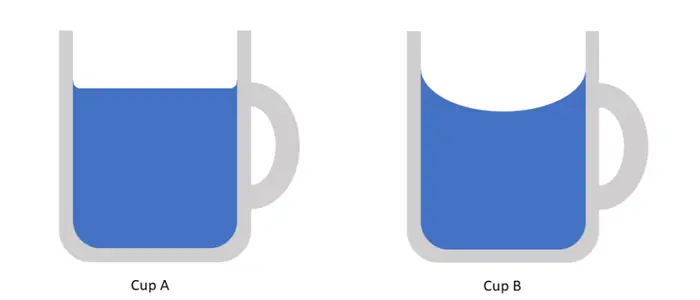
Bunu anlamak için öncelikle yukarıdaki iki bardak kesitine göz atalım. İlk bardağımızda gördüğünüz gibi sıvının yüzeyi düz, diğerinde yani B bardağımızda yüzey kavisli olarak gösterilmiştir. Sizce bu bardaklardan hangisi bir karıştırma anını temsil etmektedir? Tahmin ettiğiniz gibi cevap ikinci yani B bardağıdır. Aslında bir sıvıyı karıştırmayı bıraktığımızda yüzeyi anında düzleşmez. Düzleşmeden önce bir süre bu biçimde kavisli kalır.
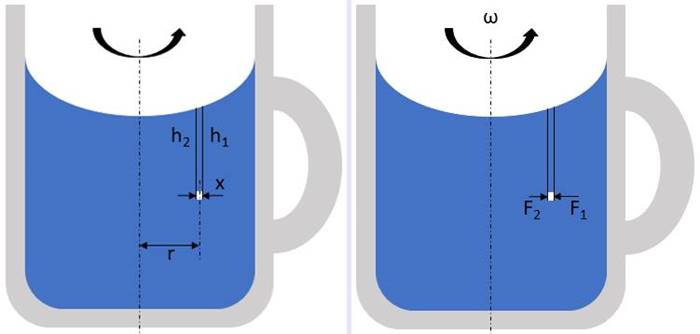
Şimdi çayımızın içinde çok küçük bir parçacık olduğunu düşünelim. Aşağıdaki görselde beyaz renk ile gösterilen bu parçacığın konumuna dikkat edin. Gördüğünüz gibi aslında köşelerinin derinlikleri aynı değildir. Sonuçta sıvılarda derinlik basınç ile orantılıdır. Derinlik arttıkça tanecik üzerindeki basınç da artacaktır. İşte bu derinlik farkından dolayı da bu parçacık üzerindeki kuvvetler eşit olmayacaktır.
Bu nedenle, sıvı elemana etki eden net kuvvet F₁−F₂ biçimindedir. Bu da bu parçacığa dairesel hareketi için gerekli merkezcil ivmeyi sağlar. Bu durum elbette sıvıdaki tüm parçacıklar için geçerlidir. İşte bu dönme sonucunda sıvının akışında bir değişiklik ortaya çıkar.
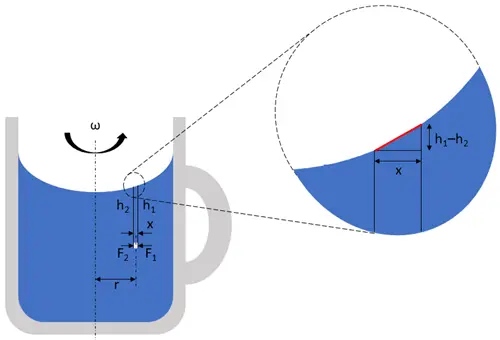
Sıvıdaki nesnelerin dairesel hareketteki merkezcil ivmesi rω² olarak ifade edilir. Burada r, nesnenin eksene olan mesafesi ve ω, açısal dönme hızıdır. ( Açısal hız, bir objenin birim zamandaki açısal olarak yer değiştirme miktarına verilen isimdir.) Aşağıdaki görselde dönme esnasında bu temsili nesnemize neler olduğunu daha yakından inceleyelim. Görselde h₁-h₂/x ile ifade edilen eğimdir. ( kırmızı çizgi). Eğer ω (açısal hız) sabitse, h₁-h₂/x eğimi artar bunun sonucunda kenarlar yükselir, orta daha çukur hale gelir.
Tanecikler Neden Ortada Toplanır?
Biraz önce de aktardığımız gibi, sıvıyı karıştırmayı bıraktığımızda yüzeyi anında düzleşmez. Düzleşmeden önce bir süre kavisli kalır. Şimdi karıştırmayı bıraktığımız anda iki farklı çay taneciğinin konumlarına göz atalım. Bunlardan bir tanesi dibe çökmüş olsun. Diğeri ise yüzeye daha yakın konumda. Sizce bu ikisi aynı açısal hızla mı dönmektedir?
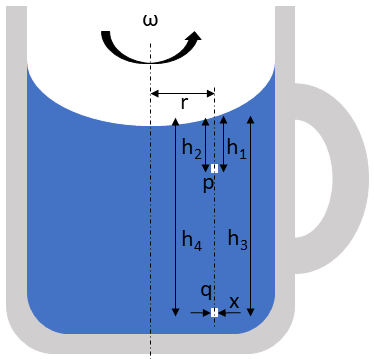
Cevap hayır. Bardağın tabanıyla sıvı arasında sürtünme olduğu için sıvının üstteki dairesel hareketi aşağıdan daha hızlıdır. Sıvıyı karıştırdığımızda, sıvı hemen dağılıp bardağın duvarına çarpacaktır. Bu yüzden bardağın çevresindeki basınç, ortaya göre daha fazla olur.
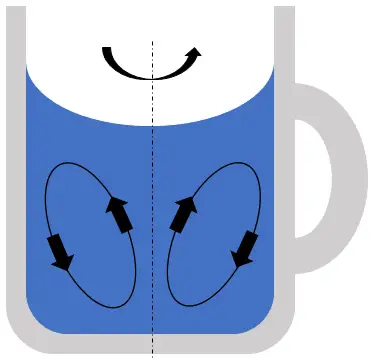
Ancak bu, bardağın tabanı için doğru değildir. Bardağın tabanındaki sürtünmeden dolayı alt taraftaki sıvı durağandır. Bu yüzden alt kısım için bardağın çevresindeki basınç ile ortasındaki basınç arasında fark olmaz. Ancak üst kenardaki basınç, sıvıyı aşağıya itecektir. Bu süreç sonucunda da aşağıdaki görselde de gördüğünüz gibi çay yapraklarının merkeze yakın toplanmasını sağlayan girdaplar oluşur. Bu girdapların oluşması nedeni sebebi, sıvıyı karıştırdığımızda bardakla sıvı arasında oluşan sürtünmedir .
Sonuç Olarak;
Yukarıdaki süreç çay yaprağı paradoksunun yani çay parçacıklarının ortada toplanmasının basit bir açıklamasıdır. 1926’da Albert Einstein bu davranış için ilk matematiksel açıklamayı yaptı ve nehir kıyılarının aşınmasını açıkladığı, Baer yasasını reddettiği makalesinde yayınladı. Onun bu çözümü, atmosfer hareketlerini ve erozyonu daha iyi anlamamızda da faydalı olmuştur.
Sık deneyimlediğimiz ancak adını ve nedenini tam olarak bilmediğimiz bir başka ilginç durum için göz atınız: Bir Paket Kuruyemişteki Fizik: Brezilya Fındığı Etkisi Nedir?
Kaynaklar ve ileri okumalar:
- Yazıdaki hesaplamaların detayları için: Why Do Tea Leaves Gather At The Center Of A Cup After Stirring?; yayınlanma tarihi: 27 Ekim 2020; Bağlantı: https://medium.com/
- Tea leaf paradox; https://en.wikipedia.org/wiki/Tea_leaf_paradox
- Yukarıda aktardığımız fenomeninin güzel bir örneğini izlemek isterseniz: Tea leaf paradox experiment; Bağlantı: Tea leaf paradox experiment
- Bu fenomenin arkasındaki bilimin yol açtığı şaşırtıcı bir ilerleme için: For Fluid Equations, a Steady Flow of Progress; Yayınlanma tarihi: 13 Ocak 2020; Bağlantı: For Fluid Equations, a Steady Flow of Progress;/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





