Mühendislik tarihinin en büyük başarılarından biri, geçilmesi imkânsız görünen nehirleri ve boğazları birbirine bağlayan köprülerin inşa edilmesidir. Bu köprülere baktığınızda, hepsinde ortak bir şeklin öne çıktığını fark edersiniz: İngilizcede catenary olarak bilinen ve Türkçeye zincir eğrisi olarak çevrilen özel bir eğri formu.

Bir zinciri iki kancadan sarkıtıp kendi ağırlığı altında serbestçe asılı bıraktığınızda, oluşan eğriye zincir eğrisi (catenary) denir. Herhangi bir asılı zincir, doğal olarak bu denge şekline ulaşır. Bu formda, zinciri yukarıda tutan gerilme kuvvetleri ile zinciri aşağı çeken yerçekimi kuvveti tam olarak birbirini dengeler.
Bir zincir eğrisini ters çevirdiğinizde ortaya çok güzel bir şey çıkar. Ters çevrilen zincir eğrisi bir kemer oluşturur ve bu, bir kemerin sahip olabileceği en dengeli şekil olarak kabul edilir. Asılı duran bir zincirde, gerilme kuvvetleri eğri boyunca ilerler. Eğriyi ters çevirdiğinizde ise bu gerilme kuvvetleri, sıkıştırma kuvvetlerine dönüşür.

Bu sıkıştırma kuvvetleri kemerin hattı boyunca yönlendirildiği için kemer eğilmez veya bükülmez. Eğer bir kemer inşa etmek istiyorsanız, mutlaka bir ters zincir eğrisi formunu temel almalısınız. Böylece yapı, yalnızca kendi ağırlığıyla serbestçe ayakta durur. Aynı zamanda minimum miktarda malzeme kullanarak inşa edilebilir.
İngiliz mimar Robert Hooke, zincir eğrisini matematiksel olarak inceleyen ilk kişidir. 1675 yılında, bu eğrinin yapısal önemine dikkat çekmiş ve eğik duran bir zincir eğrisinin ters çevrildiğinde, kendi ağırlığı altında eğilip bükülmeden durabilen en dengeli kemer formunu oluşturduğunu anlatmıştır.

Peki Bir Zincir Eğrisini Döndürürsek Ne Olur?
Katenoid, serbestçe asılan bir zincirin oluşturduğu eğrinin — yani zincir eğrisinin — bir eksen etrafında döndürülmesiyle ortaya çıkan geometrik bir yüzeydir. Bu dönüş hareketi sonucunda oluşan yüzey, hem estetik açıdan göze hitap eden formuyla hem de fiziksel olarak taşıdığı yapısal özelliklerle dikkat çeker. Bu yüzden katenoid, matematikçiler ve mühendisler için uzun yıllardır ilgi çekici bir inceleme konusudur.
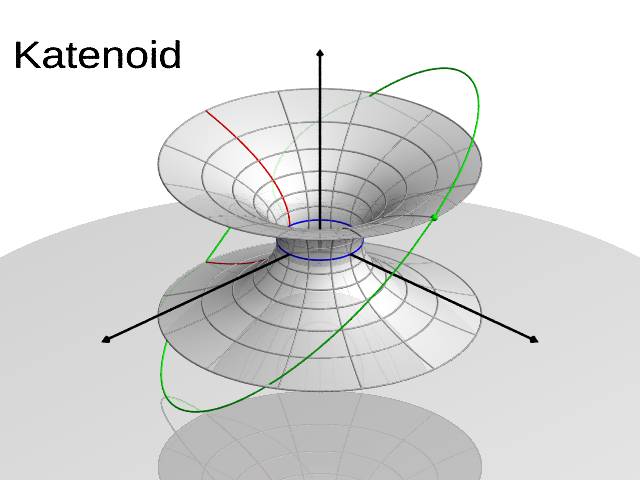
Katenoid, 1744 yılında İsviçreli matematikçi Leonhard Euler tarafından keşfedildi. Euler, bu yüzeyin bir minimal yüzey olduğunu kanıtladı. Yani, belirli bir sınır verildiğinde, o sınırı kaplayan en küçük yüzey alanına sahip form katenoidtir.
Bu özelliği en güzel şekilde sabunla gözlemlemek mümkündür. İki dairesel halka arasında gerilen sabun filmi, doğal olarak bir katenoid şekli alır. Çünkü sabun filmi, yüzey alanını minimumda tutmaya çalışır.
Katenoidi özel kılan bir diğer önemli nokta ise şudur. Düzlem dışında, bir eğrinin döndürülmesiyle oluşabilen tek minimal yüzey olmasıdır. Bu da onu hem teorik matematikte hem de fiziksel modellemelerde eşsiz kılar.
18. yüzyıldan bu yana, zincir eğrileri mimaride büyük bir ilham kaynağı olmuştur. Çünkü bu eğriler, kuvvetleri dengeli bir şekilde dağıtarak özellikle kemer yapıları için son derece ideal bir form sunar.
Catenary kemerlerine birçok kilise ve katedralde rastlanabilir. Aynı zamanda bu form, Barselona’daki La Pedrera gibi mimari başyapıtlarda da karşımıza çıkar. Bu yapı, vizyoner mimar Antoni Gaudí tarafından tasarlanmıştır. Gaudí, zincir eğrisinin doğal dayanıklılığını ve estetik yapısını benimseyerek, hem görsel açıdan çarpıcı hem de yapısal olarak verimli tasarımlar üretmiştir.

Sonuç olarak
Katenoid ve zincir eğrisi, bugün hâlâ matematikçiler ve mimarlar için hayranlık uyandıran formlar olmaya devam etmektedir. Çünkü bu iki yapı, işlevsellik ile zarafeti olağanüstü bir şekilde bir araya getirir.
Kaynaklar ve ileri okumalar:
- Maths in a minute: The catenary; Yayınlanma tarihi: 5 Aralık 2016. Kaynak site: Plus math. Bağlantı: Maths in a minute: The catenary/
- Carlson, Stephan C.. “catenary”. Encyclopedia Britannica, 22 Mar. 2024, https://www.britannica.com/science/catenary. Accessed 29 April 2025.
- Prof. Dr. Ali Sinan Sertöz; En Kısa Zaman Eğrisi; Bilim ve Teknik Mart 2017
- These Mysterious Shapes Are at the Heart of Intriguing Mathematical Problems. Yayınlanma tarihi: 15 Nisan 2025. Kaynak site: Bağlantı: Scientific American.These Mysterious Shapes Are at the Heart of Intriguing Mathematical Problems
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





