Havada top çevirmek kolay bir iş değildir. Ancak ardında yatan matematik aslında aktivitenin kendisinden çok daha karmaşıktır.

1970’li yıllarda günümüzde kendisinden sıkça bilgi teorisinin babası olarak bahsettiğimiz matematikçi ve elektronik mühendisi Claude Shannon (1916-2001) aynı zamanda usta bir hokkabazdı. Onun bu hobisi 1980’lerin başında, topların havada kalma süresi ile her bir topun elinde ne kadar süre kaldığını ilişkilendirmesine ve devamında da havada top çevirmek ile ilgili ilk resmi matematiksel teoremini yayınlamasına neden oldu.
Ancak aslında bu havada top çevirmek ile ilgili ilk bilimsel inceleme değildir. Çok daha önceleri, 1903’te Edgar James Swift konu ile ilgili bir öncü çalışma yapmıştı.
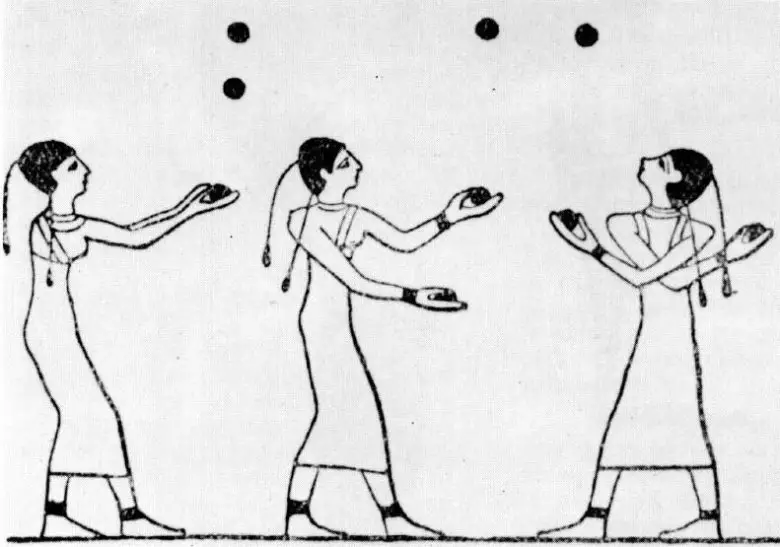
Shannon’ın top çevirme denklemi (F+D).H=(V+D).N biçimindeydi. (F: bir topun havada kaldığı süre; D: bir topun elde kaldığı süre; H: kullanılan el sayısı; V: bir elin boş kalma süresi; N: kullanılan top sayısı). Shannon’ın denklemi, bir hokkabazın el hızının önemini göstermekteydi.
Sonraki yıllar içinde matematikçiler hokkabazlık sanatının yapısını ciddi bir biçimde incelemeye başladılar. Bunun için de üst düzey bir matematik kullanmak zorunda kaldılar. Paul Klimek, Bengt Magnusson, Bruce Tiemann, Adam Chalcraft, Mike Day ve Colin Wright havada top çevirme ve matematik ilişkisi üzerine çalışmalar yapan matematikçilerden bazıları oldu. Sonunda da bazı şablonlara ulaştılar.
Siteswap Nedir?
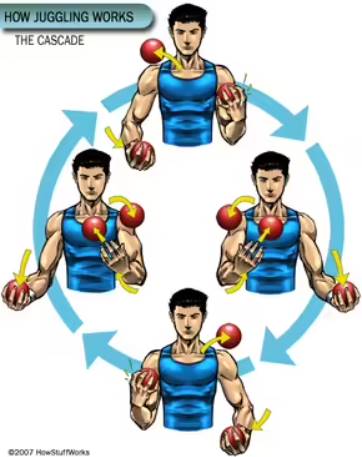
Havada top çevirme, esasen periyodik döngülerde klasik bir parabolik hareketi takip ederler. Oyunda birden fazla nesne vardır ve nesne sayısı arttıkça olay karmaşıklaşır. Siteswap her atışa bir sayı atayarak hareketi kodlamaya yarar. Örneğin 3 sayısı, çene hizasına kadar giden ve kabaca üç vuruş boyunca havada kalan bir atışı temsil eder.

Sonuçta acemilerin çoğu, üç top ile oynamayı öğrenerek işe başlar. Dolayısıyla 3-3-3 biçiminde olan bir sitewap denklemi 3 tane topun ( 3-3-3’ün ortalaması 3’tür) iki el arasında aynı yükseklikte atılıp tutulduğunu ifade eder. 6 ise 6, 3’ün yaklaşık iki katı kadar havada kalan bir kafa üstü atıştır. Tek sayılı atışlar bir elden diğerine geçer. Çiftler aynı el tarafından hem atılır hem de yakalanır. A 2, tutulan bir toptur ve 0, boş bir eli belirtir.
Bu Sayılar Ne İşe Yarar?
Tempo ne olursa olsun, bir hokkabazın eli bir seferde yalnızca bir atış yapacaktır. Bu, belirli bir atış dizisindeki sayıların ortalamasının her zaman atılan topların sayısına eşit olması gerektiği anlamına gelir. Yani siteswap diziliminde, belirli bir dizi oluşturan sayıların ortalaması daima oynatılan topların sayısına eşit olmalıdır. Örneğin 6-6-1-5-1-5 dizinin ortalaması 4 olduğundan belirtilen atışları takip eden bu diziyi oynamak için dört adet topun kullanılması gerekmektedir.
Ortalamaların kullanılması sayesinde üç topun tam olarak aynı yükseklikte sağ ve sol eller arasında ileri geri hareket ettiği bir rutin, 4-4-1 gibi bir dizilimle yer değiştirilebilir. Sonuçta her ikisinin de ortalaması aynıdır. Bu sayılar elbette topların yörüngesi ya da ellerin hareketi konusunda kesin bir bilgi vermez. Yine de bu şablonları birbiri ile paylaşan hokkabazlar için önemli araçlardır.
Ancak siteswap, matematik ile hokkabazlığı bütünleştirmek için aslında sadece bir başlangıçtır. Günümüzde hokkabazlık ile ilgilenen matematiğin daha bir çok alt dalı mevcuttur. İlk olarak eğlence ve ilgi çekmek amacı ile işe başlanmış olsa da şimdilerde hokkabazlık matematiği üst düzey matematik ve bilgisayar programlama bilgisi gerektirmektedir. Bu arada hatırlatalım. Hokkabazlık sadece matematikçilerin ilgisini çekmez. Hareketlerin arka planındaki sürecin anlaşılması için sinirbilim de konu ile ilgili araştırmalar yapmaktadır. Bu nedenle hokkabazlık insan hareketi ve algı arasındaki ilişkinin anlaşılması açısından bir çok deneyde rol oynamıştır.
Kaynaklar ve ileri okumalar için:
- The Mathematics of Juggling; Yayınlanma tarihi: 24 Mayıs 2017; Bağlantı: https://www.quantamagazine.org
- The Mathematics of . . . Juggling; Yayınlanma tarihi: 3 Kasım 2004; Bağlantı: https://www.discovermagazine.com/
- How Juggling Works; Bağlantı: https://entertainment.howstuffworks.com/juggling.htm
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel