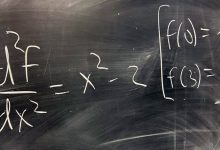Matematik nedir? Neden matematik öğrenmek zorundayız? Matematiği kim buldu da başımıza bu dertleri açtı? Bu ve buna benzer sorular, matematik ile ilgili sorun yaşayan her öğrencinin aklına gelir.

Oysa ki bazı soruların cevaplarını vermek kolay değildir. Yukardaki sorularda bunlara dahildir. Tarih boyunca insan dünyanın temel işleyişini anlamaya uğraştı. Sürekli olarak içinde bastıramadığı merak duygusu ile çevresindeki nesnelerin özelliklerini belirleyen kuralları ve birbirleriyle olan ilişkilerini keşfetmek istedi. İşte keşfetmeye çalıştığı bu düzen aslında matematikti.
Matematiğin bir keşif mi yoksa icat mı olduğu sık sık gündeme gelir. Kimilerine göre matematik insanın soyut düşünebilme yeteneğinin bir sonucu olarak insan beyninin bir icadıdır. Kimileri içinse matematik zaten dünya düzeni içine kodlanmış durumdadır. Aslında matematik hem keşif hem de icattır. İnsanlar önce matematiksel kavramları çevrelerindeki dünyadan soyutlayarak icat etmişler, sonra da icat ettikleri kavramlar arasındaki karmaşık bağlantıları keşfetmişledir.
Matematik Nedir?
Tanım olarak ele alındığında matematik şekil, nicelik ve düzenin mantığıyla ilgilenen bilimdir. Kavram olarak Eski Yunanca “medeis” ya da “matesis” kelimesi “matematik” kelimesinin köküdür ve “ben bilirim” anlamına gelmektedir.
Daha sonra sırasıyla “bilim, bilgi ve öğrenilmesi gereken şey” gibi anlamlara gelen “μάθημα (máthema)” sözcüğünden türemiştir. “Μαθηματικός (mathematikós)” “öğrenmekten hoşlanan” anlamına gelir. “Matematik” sözcüğü Türkçeye Fransızca “mathématique” sözcüğünden geçmiştir.
Matematikteki yenilikler kültürel değişiklikleri yönlendirmiştir. Kültürel gereksinimler matematikteki gelişmelerin yönünü çizmiştir. Bunun sonucunda tarih boyunca matematik ve kültür birlikte gelişmiştir. Yunan, Arap ve Hintli matematikçilerin trigonometrideki buluşları olmasaydı, ünlü denizcilerin engin okyanusları aşarak altı kıtaya açılması çok daha tehlikeli olurdu. Çin’den Avrupa’ya ya da Endonezya’dan Yeni Dünya’ya uzanan ticaret yollan, gözle görülmeyen matematiksel ipliklerle birbirine bağlanmıştı.
Matematiği İlk Kim Buldu?
Matematiği kim buldu? sorusu doğru bir soru değildir. Çünkü bu soru için tek bir cevap yoktur. Matematiğin kökeninin ne olduğu meselesi matematikçiler, matematik tarihçileri ve felsefeciler arasında sıklıkla tartışılan bir konudur.

Matematik tarihçileri, matematiğin temeli olan sayı kavramını genellikle doğa ile nesneler arasında kurulan birebir eşleşme olarak kabul ederler. Buna kanıt olarak da sayma çömlekleri ve sayma kemiklerini (çetele çubuklarını) gösterirler.
Yukarıda gördüğünüz 1970’lerde Güney Afrika’da keşfedilen Lebombo Kemiği (MÖ 44.200 – 43.000) ve 1960’larda Kongo’da bulunan İshango ( İşhango) Kemiği (MÖ 20.000 – 18.000) bu sayma kemikleri arasında bir adım öne çıkmaktadır.
Ancak matematiğin matematik olarak incelenmesi M.Ö 6000’li yıllar civarındadır. Bir çok kaynakta Mısır Nil Nehri kıyıları, matematiğin ilk ortaya çıktığı yer olarak kabul edilmektedir. Ancak yapılan araştırmalar aslında aynı anda dünyanın farklı bölgelerinde de matematiksel uyanışların başladığını göstermektedir.

Çin, Hindistan, Orta Amerika ve Mezopotamya’daki çeşitli medeniyetler, günümüzde kullanılan matematiğe pek çok katkı sağladı. Bu katkıları da birbirinden bağımsız yaptılar. Kısacası matematik, kimse tarafından bulunmamıştır. Farklı dilleri konuşan, farklı kültürlere sahip çok sayıda insanın çabalarının bir araya gelmesiyle gelişmiştir.
Neden Matematik Öğreniyoruz?
Günümüzde matematik, tüm dünyada doğa bilimleri, mühendislik, tıp ve sosyal bilimler dahil olmak üzere birçok alanda temel bir araç olarak kullanılmaktadır. Uygulamalı matematik, matematiksel bilginin diğer alanlara uygulanmasıyla ilgili matematik dalıdır. Yeni matematiksel keşiflere ilham verir ve bunlardan yararlanır. Bazen tamamen yeni disiplinlerin gelişmesine yol açar.

Uygulamalı matematiğin tam tersi olmasa da, saf matematik, gerçek dünya problemlerinden ziyade soyut problemleri ile ilgilidir. Saf matematikçiler tarafından çalışılan konuların çoğunun kökleri de somut fiziksel problemlerde bulunur. ( Matematiğin bölümleri hakkında bilgi almak için bu yazıya göz atmalısınız. )
Aslında bir zamanlar “neden matematik öğreniyoruz?” sorusuna cevap vermek kolaydı. Sonucunda herhangi bir kişi, yalnızca alışveriş yaparken faturayı kontrol etmek için olsa bile, temel aritmetiği kullanır.. Marangozların temel geometriyi bilmesi gerekir. Denizciler trigonometriye ihtiyaç duyar. Ancak günümüzde matematik giderek daha görünmez hale geldi. Oysa ki arka planda bir yerde hala bizim için çalışıp duruyor.
Köşedeki kafede bulunan lüks kahve makinesi, sizi tatil yerinize götüren uçaktaki otomatik pilot ve işinizi yapmak için her gün kullandığınız bilgisayar – hepsi matematiğe bağlıdır. Aerodinamiğin matematiksel denklemleri, uçak tasarımı için hayati öneme sahiptir. Navigasyon trigonometriye bağlıdır. Yeni ilaçların geliştirilmesi, ilaçların güvenli ve etkili olduğundan emin olmak için istatistiklere dayanır.
Sonuç olarak;
Bir düşünce biçimi ve evrensel bir dil olan matematik günümüzün gelişen dünyasında birey, toplum, bilim ve teknoloji için vazgeçilmez bir alandır. Günlük yaşamda, iş ve meslekte gerekli olan çözümleyebilme, akıl yürütme, iletişim kurabilme, genelleştirme yapabilme, yaratıcı ve bağımsız düşünebilme, strateji kurma gibi üst düzey davranışları geliştiren bir alan olarak matematiğin öğrenilmesi kaçınılmazdır.
Web sitemiz Matematiksel aslında yazıda ele aldığımız tüm sorulara cevap vermek adına kurulmuştur. Bu nedenle konu hakkında merak ettiğiniz diğer şeyleri sitemizde yapacağınız aramalar ile bulabilirsiniz. Ayrıca daha fazla bilgiye bu bağlantıdan erişebilirsiniz. Unutmayalım. Godfrey Harold Hardy’nin de dediği gibi “Dünyadaki en masum uğraş, matematiktir. “
Kaynaklar ve İleri okumalar:
- What is Mathematics; Bağlantı: https://www.tntech.edu
- What is mathematics?; Yayınlanma tarihi: 11 Kasım 2021; Bağlantı: https://www.livescience.com/
- The unreasonable relationship between mathematics and physics. yayınlanma tarihi: 3 Nisan 2018; Bağlantı: https://plus.maths.org/
Matematiksel