Bir strateji oyunu olan satranç sadece günümüzde değil tarihin hemen her sürecinde önem taşımaktaydı. Hatta belli bir dönem o kadar popüler hale geldi ki, matematikçiler fikirleri aktarmak için bu oyunu kullandılar.

O dönemin en ünlü satranç bulmacalarından biri 1256 yılında, tarihçi ve biyografi yazarı İbn Hallikan ( Khallikan / 1211–1282) tarafından kaleme alınmıştır. Ancak bu anlatı muhtemelen 5. yüzyılda Hindistan’da ortaya çıkan daha eski bir versiyonun yeniden yorumlanmasıdır.
Hikayeye göre, satrancın mucidi olarak bilinen Sissa ben Dahir, bir gün hükümdarı Kral Sharim’in huzuruna çağrılır. Kral yeni keşfedilen satranç oyunundan çok memnundur. Bu nedenle de Sissa’ya istediği herhangi bir ödülü vermeyi teklif eder. Sissa da biraz tahıl ister.
Bu mütevazi istediğini de 8 × 8 satranç tahtasındaki kareleri kullanarak açıklar. İlk başta bir buğday tanesini (hikayenin bazı versiyonlarında pirinç) satranç tahtasının sol alt karesine yerleştirir. Sonrasında bir sonraki kareye geçer ve buraya da iki buğday koyar. Devamında aynı biçimde devam eder. 4,8,16,32… biçiminde buğday tanelerini sırasıyla satranç karelerine yerleştirir.
Önemsiz bir ödül gibi görünen şeye şaşıran kral, tahılların sayılmasını emreder. 8. karede 128 tane, 24. karede 8 milyondan fazla ve satranç tahtasının ilk yarısındaki son kare olan 32. karede 2 milyardan fazla buğday tanesi vardır. Ve satranç tahtasındaki buğday sayısının toplamı da 18 446 744 073 709 551 615 yani (264 – 1) kadardır. (on sekiz kentilyon dört yüz kırk altı katrilyon, yedi yüz kırk dört trilyon, yetmiş üç milyar, yedi yüz dokuz milyon, beş yüz elli bir bin, altı yüz on beş).
Bu sayının değeri o kadar büyüktür ki, bu kadar çok buğdayın hasat edilmesi mümkün değildir. Aslında bu sayı 2020-21 döneminde yıllık dünya buğday üretiminin 2.000 katından fazladır. Aslında hikayenin iki alternatif sonu vardır: Birinde kral, Sissa’yı baş danışmanı yapar. Diğerinde ise, Sissa, kralı aptal gibi gösterdiği için idam edilir.
Buğday ve Satranç Tahtası Sorusu Ne Anlama Gelir?
Aslında muhtemel aktardığımız bu hikayeyi satrancın tarihi ile ilgili bir yerlerde okumuşsunuzdur. Olaya dahil olan kişiler farklı olsa da özünde verilen mesaj hepsinde aynıdır.

Sissa’nın bu isteği aslında her ardışık terimin bir öncekinin iki ile çarpıldığı ve sonucunda toplamın 1 + 2 + 4 + 8 + 16, vb. gösterildiği geometrik seri olarak bilinen şeye güzel bir örnektir. Bu örnek üstel büyümeyle sayıların ne kadar hızlı artabileceğini de bize hatırlatır.
Peki Buğdayın Asal Sayılar İle İlgisi Nedir?
Öklid asal sayıların sonsuza dek sürdüğünü kanıtladığından beri, matematikçiler daha büyük ve daha büyük asal sayılar üretebilecek akıllı formüller arayışındaydı. Bu formüllerin en iyilerinden biri, Marin Mersenne adlı bir Fransız keşiş tarafından bulunacaktı. Bu formülün sırrı, buğday ve satranç tahtası hikayesinde gizlidir.
Günümüzde p doğal sayısı için 2p – 1 şeklindeki sayılara Mersenne sayıları, bunların asal olanlarına da Mersenne asalları denir. Sebebi, Mersenne’in 1644 tarihli Cogitata Physica-Mathematica adlı eserinde 257’ye kadarki tüm p değerlerinden sadece p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 ve 257 değerlerinin bize asal sayı verdiğini iddia etmesidir.
Her kareden bir tane buğday çıkartırsak sonuç Mersenne’nin formülü olan (2n −1) olur. Görünüşe göre bunu, her karenin asallığını test etmek için kullanabiliriz. Aşağıdaki görselde gölgeli karelerde asal sayıları görebilirsiniz. Ayrıca bu işaretli kutulara kadar olan kutulardaki sayıların toplamlarının bazıları bu asal sayıya eşit olacaktır. Örneğin ilk üç karenin toplamı 1 + 2 + 4 = 7 ( 23-1) asaldır. Aynı biçimde ilk beş karenin toplamı 1 + 2 + 4 + 8 + 16 = 31 ( 25-1) asaldır.
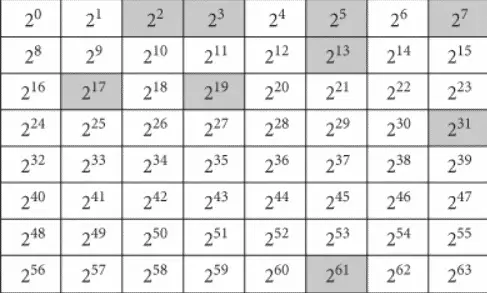
Mersenne bu kuralı genelleyebileceğini düşündü. Çünkü bu genellemeyi yapabilirse büyük bir sayının asal olup olmadığını anlamanın bir yolunu bulacaktı. Mersenne ve matematik için ne yazık ki bu fikri pek işe yaramadı. Satranç tahtasında 11. kareye baktığınızda, o noktaya kadar toplam 2047 pirinç tanesi var. 2047 bir asal değil çünkü 23 × 89’a eşit. Ancak Mersenne’in fikri her sayı için işe yaramasa da keşfedilen en büyük asal sayılar bulunmasında günümüzde hala geçerliliğini koruyor.
Kaynaklar ve İleri okumalar:
- Wheat and chessboard problem; https://en.wikipedia.org/
- Math Adventures/Wheat and the Chessboard; https://en.wikiversity.org/
- Bardi, Alberto. (2021). Mathematics and Cultures Across the Chessboard: The Wheat and Chessboard Problem. 10.1007/978-3-319-57072-3_82.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






