Eminiz ki matematik dersinde “Bu benim ne işime yarar? diye düşündünüz zamanlar olmuştur. Sanal sayılar ile ilk karşılaştığınızda kendinize bu soruyu sormuş olmanız da olasıdır. Ancak sanal sayılar ve tanımlamaya yardımcı oldukları karmaşık sayılar, fizik, mühendislik, sayı teorisi ve geometride geniş kapsamlı bir etkiye sahipler.

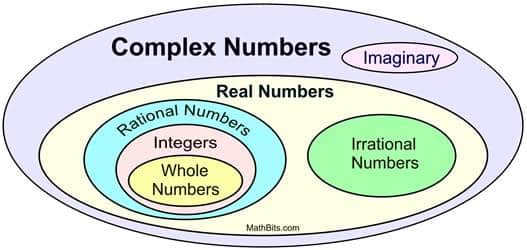
“Gerçek sayılar” aşina olduğumuz tüm sayılardır. Gerçek sayıları toplayabilir, çıkarabilir, çarpabilir ve bölebiliriz ve bunları hem sınıflarda hem de günlük hayatımızda soruları cevaplamak için kullanabiliriz.. Ancak gerçek sayılar tüm matematik problemlerimizi çözmek için yeterli değildir.
x2=1 denklemini çözmek kolaydır. Cevabın x=1 veya x=-1 olduğunu kolayca anlayabilirsiniz. Sıra x2=-1 denklemine geldiği zaman işler biraz garipleşir. Çünkü bu sorunun cevabının -1’in karekökü diğer deyişle x=√ -1 biçiminde olur. Bu da bizi sanal sayılar fikrine götürecektir.

Karmaşık Sayılar Hayatımıza Nasıl Girdi?
1500’lerde, Girolamo Cardano polinom denklemlerini çözmeye çalışıyordu. x2-8x+12=0 gibi denklemleri çözmekte hiç zorlanmıyordu çünkü toplamı 8 ve çarpımı 12 olan iki sayıyı, yani 2 ve 6’yı, bulmak kolaydı. Bu, x2-8x+12 ‘nin (x-2)(x-6) olarak çarpanlarına ayrılabileceği anlamına geliyordu ve bu polinomu iki çarpanın çarpımı olarak ifade etmek denklemi çözmeyi kolaylaştırıyordu.
Ancak x2-3x+10=0 gibi denklemler için bunu yapmak o kadar kolay değildi. Cardono kısa sürede bunu başarmanın bir yolu olmadığını fark edecekti. Ancak √ -1 yani -1’in karekökünü içeren sayıları dikkate alırsa, bir sonuca ulaşabileceğini fark etti.
Cardano bu gerçek olmayan sayılara tereddütle yaklaştı, hatta onlarla yaptığı aritmetiği işe yaramaz olarak tanımladı. Ancak gerçek sayılarla aynı kuralların çoğuna uyduklarını görünce şaşırdı. Ve biraz zaman alsa da, Cardano’nun √ -1 ‘i gönülsüzce kullanması, gerçek sayıların güçlü ve üretken bir uzantısı olan “karmaşık sayılar”ın geliştirilmesine yol açtı.
Sanal (imaginary) sayılar adı, filozof ve matematikçi Rene Descartes tarafından 1637 yılında verildi. Devamında da Euler bu sayılara bir kimlik kazandırdı. Bu sayede de √-1 , “i” olarak gösterilmeye başlandı.
Ne olduğunu tanımlasak da karmaşık sayılar çok uzun süre boyunca bir muamma olarak kaldı. Onları hayal edebiliyor, hatta çizebiliyor ama gerçekten ne anlama geldiklerini kavrayamıyorduk. Sorun, Carl Gauss adında bir matematikçi tarafından çözülecekti. Gauss, karmaşık sayılar için a + bi gösterimini doktora tezinde resmi olarak tanıttı.
Bunun göze batan ilk sonucu; gerçek sayıların, karmaşık sayıların b’yi sıfır aldığımızda ortaya çıkan özel bir türü oluşuydu. Ancak karmaşık sayılar sadece matematiksel araçlar olarak kalsaydı, muhtemel çok fazla kişinin ilgisini çekmezdi. Neyse ki öyle olmadı.
Kuantum Mekaniği ve Karmaşık Sayılar
Karmaşık sayıların bilim insanları tarafından bile kolayca kabul görmemesinin nedeni günlük hayatımızda karşılıklarının olmadığı düşüncesinden ileri geliyordu. Ancak Michael Faraday 1830’larda alternatif akımı keşfedince karmaşık sayılar fiziksel bir gerçekliğe bürünecekti. Sonrasında da bilimsel ilerlemeler neticesinde, matematiğin ve fiziğin başka alanlarında da karşımıza çıkmaya başladı.
Günümüzde parçacık fiziği, elektrik mühendisliği gibi birçok bilimsel alan karmaşık sayılara güvenir hale geldi. Ölçülebilir büyüklüğe karşılık gelen gerçek kısmın ve ölçülemeyen gerçekliğe karşılık gelen sanal kısmın birlikteliği, evrenin küçük boyutlardaki davranışını eksiksiz olarak anlamamızı sağlamaktadır.
Gerçel sayıları kullanarak geometrik şekiller tanımlayabiliyoruz. Peki ya karmaşık sayıların geometrisi nasıl bir şey? Karmaşık geometrik şekiller tanımlamak için karmaşık sayıları kullanabilir miyiz? Benoit Mandelbrot’un keşfettiği üzere, cevabımız kesin bir “evet”. Karmaşık sayılardan doğan garip şekillerin çizimine dair yaptığı çalışma, ilk bilgisayar grafik çalışmaları arasındadır.

Günümüzde Mandelbrot’un fraktalleri, Mandelbrot kümeleri olarak bilinir. Şekilleri, denklemdeki uzunlukları ikiden daha küçük değer alan karmaşık sayıların görüntüsüdür. Bu şekiller bilgisayarların oluşturduğu belki de en ünlü ve en çok bakılan görüntüler olmuşlardır.
Karmaşık Sayılarda İşlemler Nasıl Yapılır?
Karmaşık sayılarda da normal sayılarda yaptığımız bir çok işlemi yapabilirsiniz. Toplamak ve çıkarmak için, gerçek kısımları ve sanal kısımlar ile kendi aralarında işlem yapmanız yeterlidir. Karmaşık sayıların çarpımı da, dağılma özelliği yardımı ile yapılır ve elde edeceğiniz sonuç yeni bir karmaşık sayı olur.
Ayrıca karmaşık sayının ve eşleniğinin çarpımı bir reel sayıdır. Yani (a+bi). (a-bi)=a2+b2 sonucunu bize verir bu da herhangi bir karmaşık sayının tersini hesaplamamıza, dolayısıyla da bölme yapmamıza yardımcı olur. Peki tüm bunların gerçekten bir anlamı var mı?
Koordinatları (x,0) olan yatay eksende bulunan sayıları düşünün. Onları -1 ile çarpmak onları (0,0) noktasının diğer tarafına çevirecektir. Yani (1,0) noktasını -1 ile çarparsanız (-1,0) noktasını elde edersiniz. Bu nedenle -1 ile çarpmayı 180 derece döndürme olarak düşünebilirsiniz.
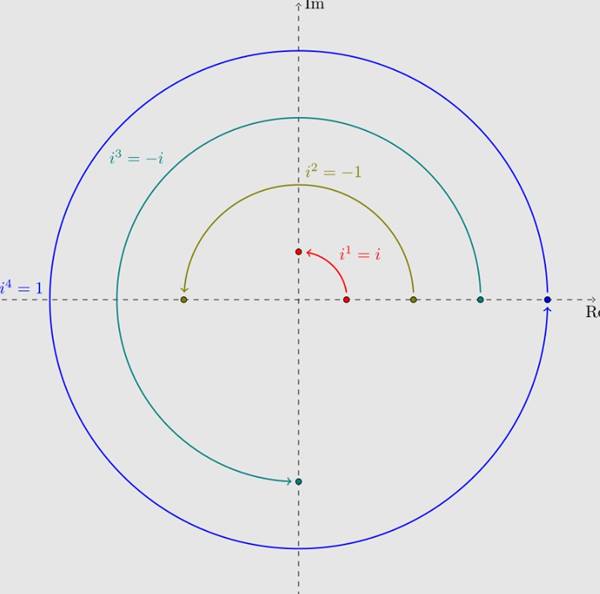
Şimdi i ile çarpmaya ne dersiniz? Aslında i ile iki kez çarpmak, -1 ile çarpmakla aynıdır. Dolayısıyla, ilki 180 derecelik bir dönüşe karşılık geliyorsa, ikincisi 90 derecelik bir dönüşe karşılık gelmelidir. Bunu aşağıdaki örnekte de görebilirsiniz.
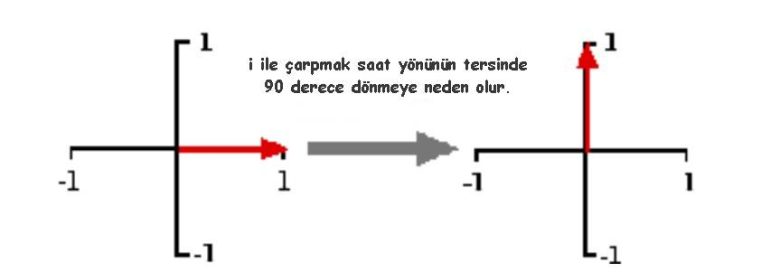
Peki ya sadece i ile değil, daha zor bir karmaşık sayı ile çarpmaya ne dersiniz? Sıradan bir pozitif sayı ile çarpma yaptığımızda koordinat düzleminde aslında ne olduğunu anımsayalım. Örneğin 2 ile çarpma sonucunda (x,y) koordinatları (2x,2y) biçimini alacaktır. Bu bir genişleme anlamına gelir. Benzer biçimde de 1/2 ile bir koordinatı çarparsanız, (0,0)’a daha yakın olan (x/2,y/2) sonucuna ulaşırsınız yani bir daralma olur. Aynı sonuç karmaşık sayılarda da geçerlidir.
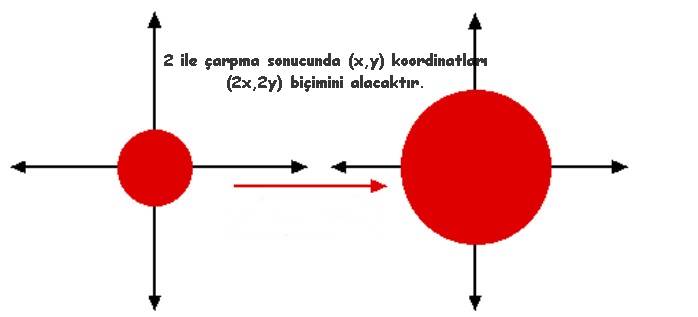
Dolayısıyla karmaşık sayılar, hayal gücünün tuhaf figürleri değildir. Aslında kendi başlarına geometrik anlamları da vardır. Sanal sayılar keşfedilecek tamamen yeni bir matematiksel dünyanın kapılarını bizlere açar. Gerçekten de karmaşıkmış dediyseniz aslında yanılıyorsunuz. Karmaşık sayılardan daha karmaşık şeyler de matematikte vardır.
Karmaşık Sayıların Dönüşlerini 3 Boyutlu Olarak Nasıl Düşünebilirsiniz?
Bu soru, William Hamilton’ı rahatsız ediyordu. Hamilton hayatının son yirmi yılını, karmaşık sayıların iki boyuttaki dönüşlerine benzer bir şekilde üç boyutlu dönüşlerini temsil etmenin bir yolunu aramaya adamıştı.

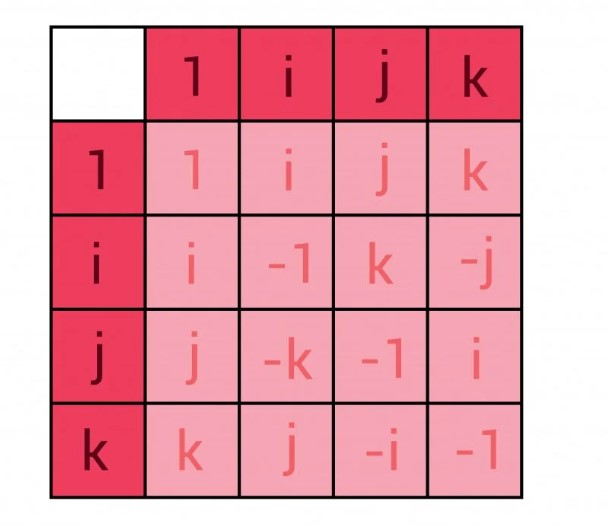
Ancak 4 boyutlu bir sayının sorunu çözeceğinin farkına varmasıyla bir aydınlanma anı yaşayacaktı. Sonucunda da kuaterniyonlar olarak bilinen bu sayıların ilk kuralını Brougham köprüsünün üzerine kazıyacaktı. Yazdığı formül şu şekildeydi: i2 = j2 = k2 = ijk = –1.
Bir kuaterniyon q ile gösterilmek üzere q=a + bi + cj + dk şeklinde yazılabilir. Burada a, b, c ve d gerçek sayılar ve i, j ve k ise sanal sayılardır. 2 boyutlu karmaşık sayılar durumunda gördüğümüz gibi, i ile çarpma sayıyı 2 boyutlu düzlemde döndürür; dördey durumunda, i, j, k’den herhangi biri veya bunların kombinasyonları ile çarpma, bir sayıyı 3 boyutta döndürür.
Her ne kadar kulağa soyut bir kavram gibi gelse de kuaterniyonlar, akıllı telefonunuzun ve tabletlerinizin dönüşünü programlamak için de kullanılır. Üstelik burada da bitmez. Gerçek sayıların ötesindeki bu uzantılar, Hamilton’un meslektaşları tarafından keşfedilen ve yedi sanal birime sahip daha da garip bir sayı sistemi olan sekiz boyutlu oktonyonlarla devam eder.
Gerçek sayıları genişleterek yarattığımız bu sistemler ile her adımda gerçek olarak düşündüğümüz şeyle de bağımızı kaybedebiliriz. Ancak kazandığımız şey, dünya hakkında düşünmenin yeni yollarıdır. Ve bunun için her zaman bir kullanım alanı bulabiliriz.
Kaynaklar ve ileri okumalar
- Maths in a minute: Complex numbers; yayınlanma tarihi: 19 Şubat 2013; Bağlantı: https://plus.maths.org
- Renou, MO., Trillo, D., Weilenmann, M. et al. Quantum theory based on real numbers can be experimentally falsified. Nature 600, 625–629 (2021). https://doi.org/10.1038/s41586-021-04160-4
- The (Imaginary) Numbers at the Edge of Reality. Yayınlanma tarihi: 25 Ekim 2018. Kaynak site: Quanta Magazine. Bağlantı: The (Imaginary) Numbers at the Edge of Reality
Matematiksel