İstatistik ve veri bilimi dünyasında olasılık dağılımları, rastgele olayları tanımlamamıza ve analiz etmemize yardımcı olan temel araçlardır. Olasılık dağılımları, önceden emin olamayacağınız birden fazla sonucu olan süreçleri tanımlamamıza yarar.

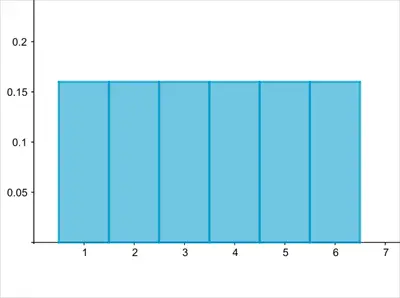
Bir örnek, bir zarın atılmasıdır. Bildiğiniz gibi 6 olası sonuç vardır. Zar adil olduğu sürece, 1 atma olasılığınız ile 6 atma olasılığınız birbiri ile aynıdır. Bu, herhangi bir sayıyı atmak için 100/6 yaklaşık 16.6 şansınız olduğu anlamına gelir. Bu da 0.166 olasılığa karşılık gelir. Bunu bir histogram kullanarak görselleştirseniz aşağıdaki gibi olacaktır. Gördüğünüz gibi her sonucun eşit olasılığa sahip olduğu olaylarda tek tip bir dağılım söz konusudur.
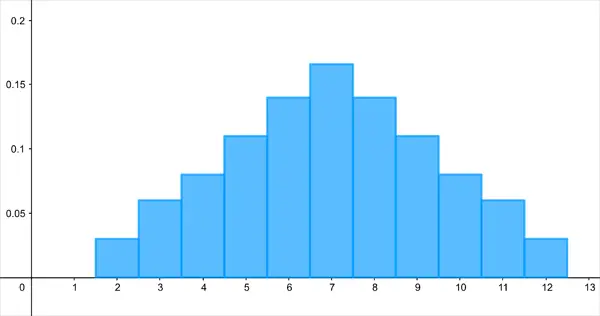
İki zar atarsanız ve gösterdikleri sayıları toplarsanız, 11 olası sonucunuz olur. (2’den 12’ye kadar olan sayılar). Ancak hepsinin olasılığı eşit değildir. Birçok farklı kombinasyon size nihai sonucu 7 (1 ve 6, 2 ve 5, vb.) verebileceğinden, 7 ile sonuçlanma olasılığınız 2 ile sonuçlanmaktan çok daha olasıdır.
Diyelim ki sokakta tanıştığınız rastgele bir kadının tam olarak 170 cm boyunda olma olasılığı nedir? Soruyu cevaplamak imkansız gibi gelecektir. Ancak neyse ki matematik size yardımcı olacaktır. Çünkü matematik size, insanların boylarının, normal dağılım denen, çan şeklindeki bir eğriyle temsil edilen bir olasılık dağılımını izlediğini söyler. Bu da bizi en ünlü olasılık dağılımına götürecektir.
Normal Dağılım (Gauss-Laplace Dağılımı) Nedir?
Ölçmeye çalıştığınız şey ne olursa olsun eğer örneklem boyutunuz yeterince büyükse, her zaman bir çan eğrisi yani normal dağılım elde edersiniz. Bu durum ilk olarak modern olasılık teorisine önemli katkılarda bulunan Abraham de Moivre tarafından gözlemlenmişti. De Moivre’nin 1756 tarihli The Doctrine of Chances (Şansların Doktrini) isimli kitabında bu konuyu açıklamıştı.
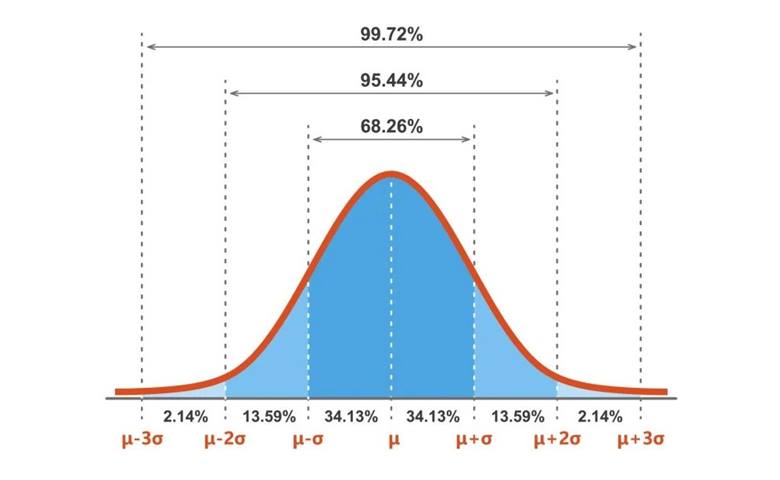
Normal dağılım, ortalamanın her iki tarafında da simetrik olan sürekli bir olasılık dağılımıdır; dolayısıyla merkezin sağ tarafı, sol tarafın ayna görüntüsüdür. Eğrinin altındaki alan olasılığı temsil eder ve eğrinin altındaki toplam alanın toplamı birdir. Normal bir dağılımda veriler ortalama etrafında kümelenme eğilimindedir ve bir değer ortalamadan ne kadar uzaksa, ortaya çıkma olasılığı da o kadar az olur.
Normal dağılım ve daha genelinde istatistikteki en önemli olasılık dağılımıdır çünkü doğadaki birçok sürekli veri grafik haline getirildiğinde bu çan şeklindeki eğriyi gösterir. Ancak daha karmaşık süreçler için başka olasılık dağılımı aileleri de vardır. Yazıda sadece çok bilinen bir kaç tanesine daha yer vereceğiz.
Bernoulli Dağılımı
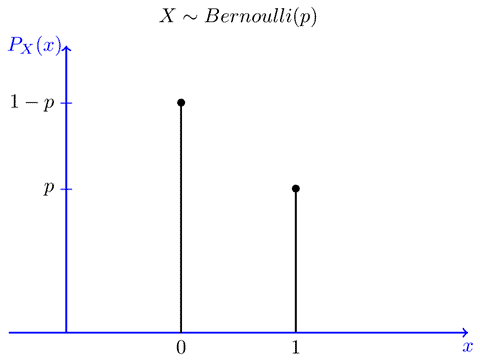
İsviçreli Matematikçi ve Fizikçi Daniel Bernoulli‘nin (1700 – 1782) adını taşıyan Bernoulli dağılımı, başarı veya başarısızlık gibi ikili sonuçları modelleyen temel bir dağılımdır. Diğer bir deyişle eğer bir olayın 2 cevabı varsa Bernoulli dağılımını oluşturur.
Dağılımda genellikle 0 başarısızlığı ve 1 başarı durumunu kategorize eder. Ziyaretçilerin satın alma işlemi yaptığı (başarılı) veya satın alma yapmadığı (başarısızlık) bir web sitesi düşünün. Bernoulli dağılımı bir ziyaretçinin satın alma olasılığını modellemek mümkündür. Aslında bu dağılım oldukça basittir; ama dağılımın önemi diğer dağılımların temelini oluşturmasıdır.
Binom Dağılımı
Binom dağılımı, sabit sayıda bağımsız Bernoulli denemesindeki (başarı ve başarısızlık) başarılı sonuçların (genellikle “k” ile gösterilir) sayısını modelleyen bir olasılık dağılımıdır. Her denemenin başarı olasılığı “p”, başarısızlık olasılığı ise “1 – p”dir.
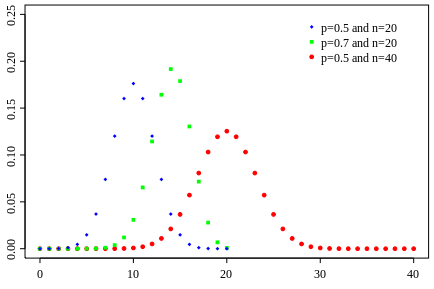
Adil bir parayı birden çok kez attığınızı hayal edin. Her yazı tura atma, iki olası sonucu olan bağımsız bir Bernoulli denemesidir. Her atışta “p” ile gösterilen başarı olasılığı (“tura gelme”) 0,5’tir. Aynı biçimde her atışta başarısızlık olasılığı (“yazı gelme”) de 0,5’tir.
Şimdi, diyelim ki, 5 atışta, belirli sayıda “tura” gelme olasılığının ne kadar olduğunu bilmek istiyorsunuz. Binom dağılımının devreye girdiği yer burasıdır. Binom dağılım formülünü kullanarak, 5 yazı-tura atışınızda belirli sayıda “tura” gelme olasılığını hesaplayabilirsiniz.
Bir tedavinin işe yarayıp yaramadığı, bir piyango biletinin kazanıp kazanmadığı gibi iki seçenekli herhangi bir olay Binom dağılımına örnek olur. Gerçek hayatta psikolojiden sosyolojiye, mühendislikten tıp alanına kadar oldukça geniş bir kullanıma sahiptir.
Poisson Dağılımı
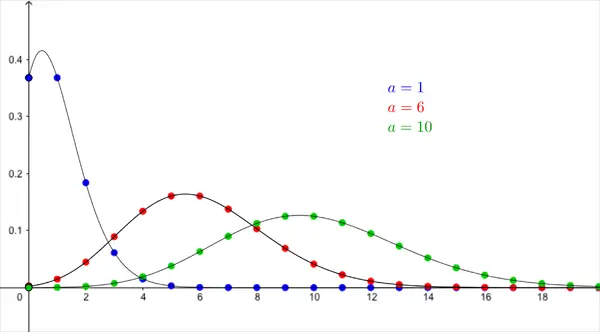
Poisson dağılımı, sabit bir zaman veya mekan aralığında meydana gelen olayların sayısını modeller. Ortalama oluşum oranını temsil eden tek bir parametre olan λ (lambda) ile karakterize edilir. 1837’de Fransız matematikçi Siméon Poisson tarafından tanıtılan bu dağılım yardımıyla çok çeşitli olasılıkları tahmin etmek mümkündür.
Bu dağılım başarı olasılığı p’nin küçük olması durumunda Binom dağılımının matematiksel anlamda basitleştirilmesidir. Belirli bir zaman aralığında ve belli bir alanda nadir görünen olayların olasılık dağılımlarında sıklıkla kullanılır. Örneğin, bir çağrı merkezine dakika başına gelen müşteri çağrılarının sayısı Poisson dağılımı kullanılarak modellenebilir. Bu dağılım söz konusu olaylar birbirinden bağımsız olduğu sürece işe yarayacaktır.
Log-Normal Dağılım
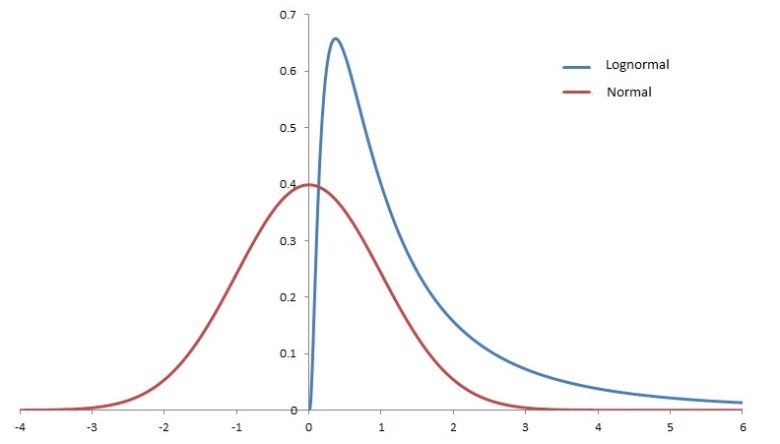
Lognormal dağılım; logaritması normal olarak dağılan bir rastgele değişkenin ayrık ve devam eden dağılımıdır. Bir başka deyişle bu dağılımda orijinal veriler normal olarak dağılmak yerine, hesaplanan bu orijinal verilerin logaritmaları normal olarak dağılır. Bu dağılım tanımı gereği sadece pozitif değerlerden oluşur. Çünkü değişkenleri ln(x1), ln(x2), ln(x3) gibi değişkenlerdir.
Lognormal dağılımının bazı yaygın kullanım alanlarına bakım veri analizlerini veya borsa veri analizlerini örnek verebiliriz. Örneğin borsada lognormal dağılım, hisse senedinin gelecekteki getirilerini tahmin etmek amacıyla kullanılmaktadır.
Sonuç Olarak
Yazımızda bu noktaya kadar karşınıza en sık çıkma ihtimali olan dağılımlardan bahsettik. Ancak daha bahsetmediğimiz onlarca dağılım olduğunu anımsatalım. Tüm bu olasılık dağılımları modern istatistiğin ve veri biliminin omurgasını oluşturur.
Kaynaklar ve ileri Okumalar:
- Maths in a minute: The normal distribution; yayınlanma tarihi: 7 Ocak 2022; Bağlantı: Maths in a minute: The normal distribution
- Maths in a minute: The binomial distribution; yayınlanma tarihi: 7 Ocak 2022; Bağlantı: Maths in a minute: The binomial distributionn
- Poisson Distribution; Bağlantı:https://www.sciencedirect.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel