Ünlü fizikçi Albert Einstein, görelilik teorisinin bir parçası olarak uzay-zaman fikrinin geliştirilmesine yardımcı oldu. Günümüzde de pek çok yerde karşımıza bu kavram çıkıyor. Peki uzay-zaman tam olarak nedir? Uzayın uzunluk birimleri ile zamanın dakikaları nasıl uyumlu olur?

Sorunun cevabını anlamak için bu ikiliğinin birlikteliğini düşünmediğimiz yüz yıl öncesine gitmeliyiz. 1915’te Albert Einstein, Prusya Bilimler Akademisi’ne genel görelilik teorisini sundu. Genel görelilik bizlere uzay ve zamanın halihazırdaki en iyi ve en isabetli açıklaması idi.
Bize madde ve enerjinin uzay ve zamanda bükülmelere ve gerilmelere yol açtığını söyledi. Hatta karadelikler ve solucan delikleri gibi egzotik uzay-zaman şekillerinin var olmasına izin veren, genel görelilik matematiği olacaktı. Genel görelilik ise, teorik fiziğinin en büyük bulmacalarından bazılarına çözümler sağlayan özel görelilik üzerine inşa edilmişti.
Uzay Zaman Tam Olarak Nedir?
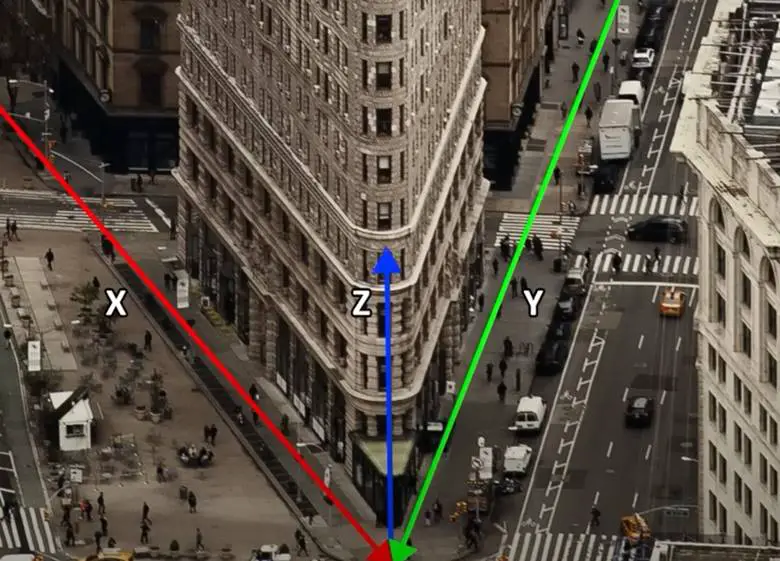
Diyelim ki iki arkadaş kahve içmek için buluşmak istiyor. Birinin diğerine tam konum vermesi lazım. Bir haritaya bakarak bunu “haritada G5’te bulunan binanın ikinci katındaki kafede buluşuruz” biçiminde arkadaşına tanımlayabilir.
Dikkat ederseniz bu tanımda üç koordinat mevcut ( G-5 ve 2. Kat). Ancak bu buluşmanın kesin biçimde gerçekleşmesi için dördüncü bir koordinat da eklememiz gereklidir. Bu 4. koordinat ise, öğleden sonra 2.00 gibi, bir zaman eklemekle mümkün olacaktır. Bu dört kavramı bir arada ele aldığımızda bir uzay-zaman olayı tanımlamış oluruz.
Uzay zamanın tanımı, uzay ve zamanda 4 sayı ile konumlanmış noktalar kümesidir. Yani alışık olduğumuz x,y,z koordinatlarına ek olarak bir de zaman koordinatı olacaktır. Ancak insan zihni dört boyutu algılayacak biçimde gelişmemiştir. Zaten fikrin anlaşılmasını zorlaştıran temel şey de budur. Şimdi biraz daha detaya inebilmek için işin arka planına göz atmalıyız.
Uzay Zaman Fikri Nasıl Gelişti?

17. yüzyılda Isaac Newton etrafımızdaki dünyanın fiziksel özelliklerini tanımlayan bir dizi denklem geliştirdi. Bu denklemler bir top atışından, gezegenlerin hareketine kadar bir çok şeyi başarıyla tanımlıyordu. Ayrıca bu denklemlerin cazip bir özelliği de vardı. Hareket edip etmemelerine bakılmaksızın tüm gözlemciler için olaylar aynı biçimde tanımlanıyor ve fizik yasaları aynı biçimde işliyordu.
Ancak 19. yüzyılda insanlar her şeyin bu kurala göre oynanmadığını fark etmeye başladı. 19. yüzyıl elektrik, manyetizma ve ışık olgularının kapsamlı bir şekilde incelendiği bir dönemdi. 1865’te James Clerk Maxwell, tüm bu olguları tek bir elektromanyetizma olgusunda birleştiren bir dizi denklem yayınladı.
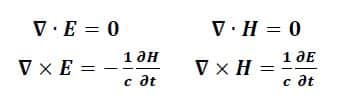
Maxwell’in keşfinden kısa bir süre sonra insanlar onun denklemlerinde bir tuhaflık olduğunu fark ettiler. Hareket etmeyen bir kişi, hareket eden bir kişiden belirgin şekilde farklı fiziksel olayları gözlemliyordu. Söz konusu sorun ışığın doğasında bir gariplik olduğuna işaret ediyordu.
Çeşitli fizikçiler, ışığın garipliklerini ve eter adını verdikleri bir ortamda yayılma olasılığını araştırdılar. Ancak hiç kimse böyle bir eter için kanıt bulamadı. Einstein’ın 1905’teki katkısı, eterin gereksiz olduğuna ve o olmadan fizik yasalarını daha iyi anlayabileceğimize işaret etmekti. Tek yapmamız gereken tamamen yeni bir uzay ve zaman anlayışını kabul etmekti.
Einstein’ın teorisi özel görelilik teorisi olarak bilinmeye başlandı. Özel görelilik bize temelde iki şey söyledi 1) Fizik yasaları ivmesiz tüm referans çerçevelerinde değişmezdir. 2) Işığın boşluktaki hızı (c), hareketinden veya söz konusu ışık kaynağının hareketinden bağımsız olup tüm gözlemciler için aynıdır.
Genel göreliliğe giden yol Hermann Minkowski ile geldi
Ancak 1907’de Einstein teorisinin tamamlanmadığını fark etti. Patent memuru olan Einstein’ın laboratuvar ekipmanına erişimi yoktu. Bunu telafi etmek için kendini düşünce deneylerine adamak zorunda kaldı. Kafasında çeşitli senaryoları değerlendirdi ve bunların üzerinden adım adım çalıştı.
Tüm bu akıl yürütme, Einstein’ı uzay-zamanın geometrisi ile uzay-zamanda meydana gelen fiziksel süreçlerin birbiriyle ilişkili olduğuna ve birinin diğerini etkileyebileceğine ikna etti. Kütleçekimi olarak algıladığımız şey yalnızca uzay-zamandaki hareketin bir sonucuydu. Tüm bu ilişkiyi ortaya koymak Einstein’ın sekiz yılını almıştı.

Özel göreliliğe kıyasla, Genel Görelilik çok daha devrimseldi. Çünkü bizi Newton’ın kütle çekimi yasasından kurtarmış ve bükülmüş uzay-zamanı ortaya koymuştu. Ancak tüm bunlara rağmen Einstein uzay ve zamanın birleştirilmesini savunacak kadar ileri gitmedi. Bu adım 20. yüzyılın başlarında Hermann Minkowski tarafından atıldı.
Minkowski uzay-zamanı nedir?
Bir zamanlar uzayın sadece büyük bir boşluk olduğunu düşünüyorduk. Ancak 1908’de Hermann Minkowski zamanın uzayın üç boyutu ile birlikte dördüncü bir boyut olarak düşünülebileceği fikrini ortaya atmıştı. Sonrasında da Einstein bu uzay zamanın nesnelerin yörüngesini ve zamanın geçişini etkileyen bir tür geometri olduğunu gösterdi.

Eviniz ve restoran gibi uzayda iki yeri düşünün. Aralarındaki mesafeyi nasıl ölçersiniz? Cevap seçiminize bağlı olsa da iki lokasyon arasındaki en kısa mesafeyi belirlemek için kuş bakışı düz bir çizgi düşünmeniz gerekecektir. Şimdi uzay-zamandaki iki olayı düşünün. A olayı “akşam 6’da evde” olmak ve B olayı da “akşam 7’de restoranda” olmak olsun. Bu iki olay arasında ne kadar zaman geçtiğini nasıl hesaplarsınız?

Bunun hileli bir soru olduğunu düşünebilirsiniz. Çünkü cevap 1 saat gibi gözükmektedir. Ancak bu modası geçmiş, Newtoncu bir dünya anlayışıyla uyumludur. Görelilik farklı bir hikaye anlatır. “Akşam 6” ve “akşam 7” aslında koordinat değerleridir yani olayların yerini belirlememize yardımcı olan etiketlerdir. “Akşam 7’de restoranda buluşalım” ile aynı anlama gelmemektedir.
Minkowski geometrisinde zaman ne anlama gelir?
Zamanın bir koordinat olarak ele alınması gerektiğini kavradıktan sonra alışık olduğumuz 3 boyutlu koordinatlar ile yaptığımız işlemleri bu dört boyutlu koordinat sistemi ile de yapmaya başlayabiliriz.
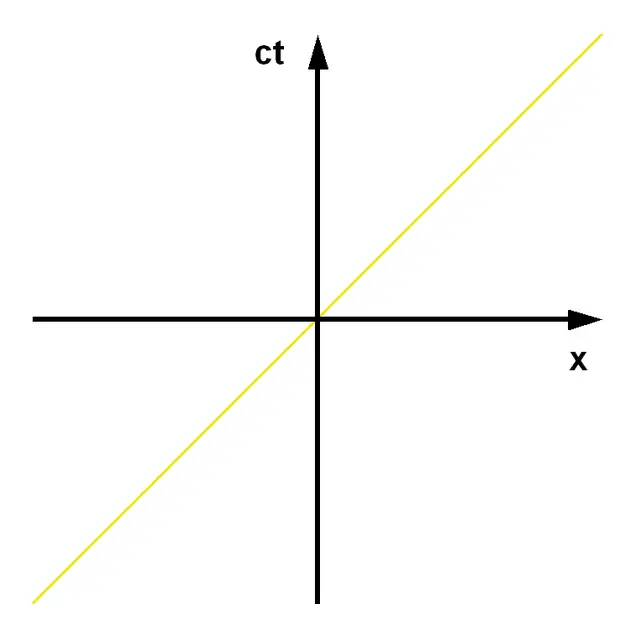
Örneğin iki nokta arasındaki uzaklığı hesaplamak için bu yeni koordinat sistemimizi kullanabiliriz. Ancak tek bir farkla. Bu iki noktamız artık belli olaylardır. Bu nedenle kullanmamız gereken geometri Öklid geometrisine değil, Minkowski geometrisine bağlı olacaktır.
Bu geometride iki nokta arasındaki düz bir çizgi sabit bir hızla seyahat etmek demektir. Ancak geçen zamanı bulmak için basit bir çıkarma işlemi yapamayız, çünkü zaman görecelidir. Hızlı hareket eden birinin algıladığı zaman ile, duran birinin algıladığı zaman aynı değildir. Bu nedenle kullanmamız gereken formül aşağıda gördüğünüz gibidir. Minkowski uzay zamanında iki nokta arasındaki düz çizgi aslında en uzun süredir.
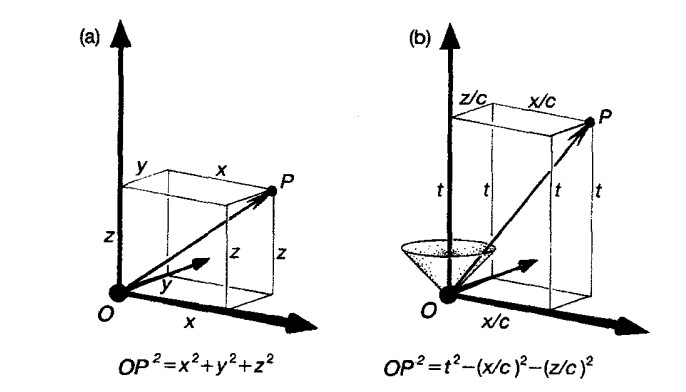
Bu nedenle uzayda ne kadar çok hareket ederseniz, zamanda o kadar az hareket ederseniz. Yani uzay zamanda A olayından B olayına kavisli bir yol izlenirse, geçen zaman düz bir çizgiye göre daha kısa olacaktır. Mantığa aykırı mı geliyor? Bu iyi. Sezgisel olsaydı, bu fikri ortaya çıkarmak için Einstein olmanıza gerek kalmazdı.
Kaynaklar ve ileri okumalar
- What is space-time?. Yayınlanma tarihi: 20 Mayıs 2021. Kaynak Livescience. Bağlantı: What is space-time?
- Spacetime: is it real and physical, or just a calculational tool? Yayınlanma tarihi: 4 Mayıs 2023. Kaynak: Big Think. Bağlantı: Spacetime: is it real and physical, or just a calculational tool?
- From Newton to Einstein: the origins of general relativity. Yayınlanma tarihi: 9 Kasım 2023. Kaynak site: The Conversation. Bağlantı: From Newton to Einstein: the origins of general relativity
Matematiksel





