Fiziksel dünyamızı Öklid uzayına uygun biçimde üç boyutlu olarak algılarız. Sonucunda algılarımıza uygun olan budur. Uzunluk, genişlik ve yükseklik biçiminde üç boyut vardır ve bir çoğumuza bu kadarı yeterlidir. Ancak pek çok problem sadece üç boyutlu uzay kullanılarak çözülemez. Bu yazımızda ele alacağımız Minkowski uzayında işin içine, dördüncü boyut olarak zaman eklenir.
Çoğumuz gibi, Einstein’ın ilk yaşamı da ona inanan insanlarla (öğretmenler, aile üyeleri ve akranlar) ama aynı zamanda onun yeteneklerine inanmayan ve onun içindeki başarı potansiyelini çok az gören birkaç önemli insanla doluydu. Ona çok da inanmayan ve hatta onun pek de sağlam bir matematik eğitimine sahip olmayan, tembel bir öğrenci olduğunu düşünen öğretmenlerinden biri de Hermann Minkowski idi.
Minkowski fiziğin matematiğine, özellikle de ışık ve maddenin etkileşimine merak sarmıştı. Einstein’ın 1905’te özel görelilik kuramını açıklaması Minkowski’yi, uzay ve zamanın dört boyutlu bir gerçekliğin bileşenleri haline getirip kendi kuramını geliştirmeye teşvik etti. Onun bu düşüncesinden ilham bulan Einstein 1915’te genel görelilik kuramını üretti, ama Minkowski bu tarihte hayatta değildi. Apandisit yırtılması nedeniyle 44 yaşında hayata veda etmişti.

Minkowski Uzayı Tam Olarak Nedir?
Einstein, iki görelilik kuramı ortaya atmıştır. Bunlardan ilki olan özel görelilik, içinde kütleçekiminin bulunmadığı bir gezegene ilişkin bir kuramdır. Einstein’ın 1905’te yayımladığı iki makalede sunulmuştur ve aslına bakarsanız sunulduğu zamanda da çok da ilgi toplamamıştır. Bilim camiasının farkındalığı Hermann Minkowski’nin 1908’de Cologne’da verdiği bir konferans sayesinde olmuştur.
Özel görelilik bize temelde iki şey söyledi. 1) Fizik yasaları ivmesiz tüm referans çerçevelerinde değişmezdir. 2) Işığın boşluktaki hızı (c), hareketinden veya söz konusu ışık kaynağının hareketinden bağımsız olup tüm gözlemciler için aynıdır. Ancak 1907’de Einstein teorisinin tamamlanmadığını fark etti.
Patent memuru olan Einstein’ın laboratuvar ekipmanına erişimi yoktu. Bunu telafi etmek için kendini düşünce deneylerine adamak zorunda kaldı. Kafasında çeşitli senaryoları değerlendirdi ve bunların üzerinden adım adım çalıştı. Tüm bu akıl yürütme, Einstein’ı uzay-zamanın geometrisi ile uzay-zamanda meydana gelen fiziksel süreçlerin birbiriyle ilişkili olduğuna ve birinin diğerini etkileyebileceğine ikna etti. Sonraki on yıl boyunca geliştirilen genel görelilik işin içine, kütleçekimini de ekleyecekti.
Ancak tüm bunlara rağmen Einstein uzay ve zamanın birleştirilmesini savunacak kadar ileri gitmemişti. Bu adım Minkowski tarafından atılmıştı. Tanımladığı uzay-zaman günümüzde Minkowski uzay-zamanı olarak biliniyor. Hem görelilik hem de kuantum alan teorisindeki hesaplamaların arka planını oluşturuyor.
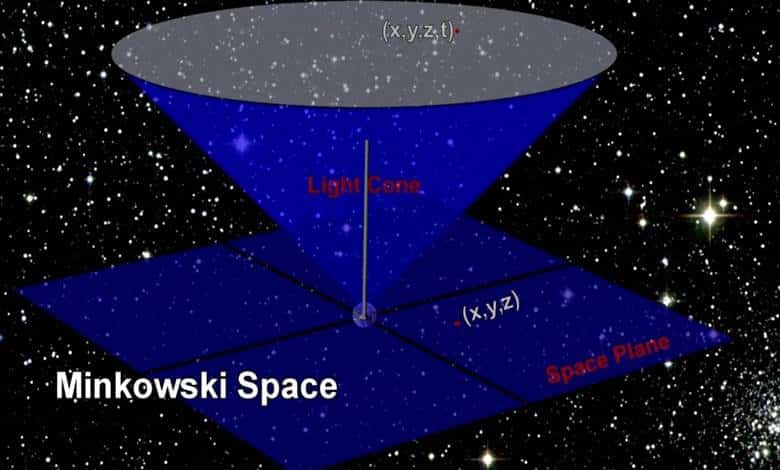
Uzay-zamanı dört boyutlu düşündüğünüzde, onun hakkında sorular sormaya başlayabilirsiniz. Mesela düz mü yoksa kavisli midir? Statik mi dinamik midir? Sonlu mu yoksa sonsuz mudur? Minkowski uzay-zamanı düz, statik ve sonsuzdur. Minkowski uzay-zamanı ile ilgili araştırma yaptığımızda da genellikle aşağıdaki görsele benzeyen bir yapı karşımıza çıkar. Buna ışık konisi denir.
Minkowski Uzayında Işık Konisi Ne Anlama Geliyor?
Işık konisi yapısı bu geometrinin önemli bir unsurudur. Bu nedenle bu ışık konisini biraz daha detaylı incelmememiz gerekecektir. Görselde üstteki koni geleceği ve alttaki koni geçmişi simgeler. Yani üst taraf bir A olayından gelecekte etkilenecek tüm olayları içerir. Benzer şekilde, geçmiş ışık konisi, A olayının geçmişi ile ilgili olaylar tanımlanmaktadır.
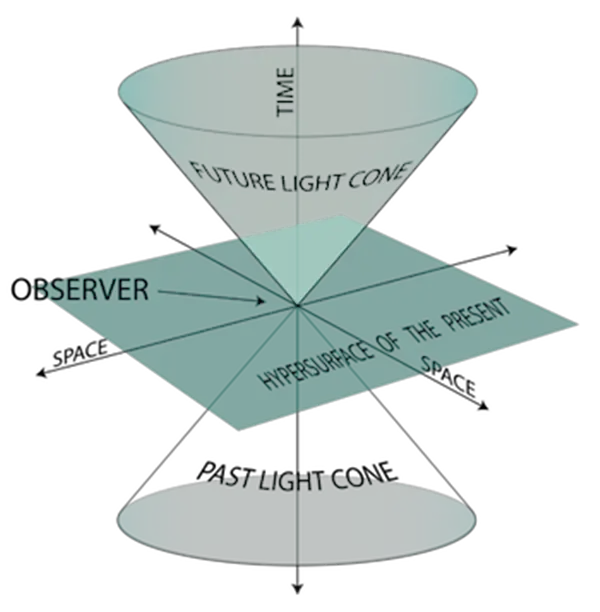
Bu ışık konisinde 4 boyut tanımlanmaktadır. Bunlardan üçü bizim alıştığımız boyutlardır. Dördüncü boyut ise zamandır. Ancak bu dört boyutu görselleştirmek kolay değildir. Çünkü insan beyni dördüncü bir boyutu algılayacak biçimde gelişmemiştir. Bu nedenle daha sezgisel hale getirmek için biri zaman olmak üzere üç boyuta indirgenmiş halini anlamak zorundayız.
Elde ettiğimiz üç boyutlu uzay zaman diyagramında, karşımıza çıkan bir başka sorun ise birimler ile ilgilidir. Zamanın birimi ile diğer boyutların birimi birbiri ile tutarlı değildir. Peki bu üçlüyü nasıl uyumlu hale getirebiliriz? Minkowski’nin bunun için bir fikri vardı. Bunun için hepimizin bildiği Yol= Hız x zaman eşitliğinden yararlandı. Ancak burada bahsi geçen hız ışık hızı olacaktı.
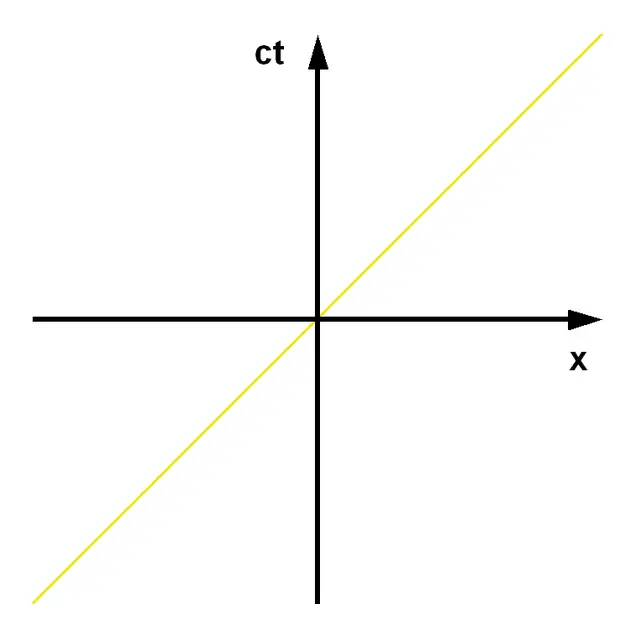
Işık hızını saniyede yaklaşık 300 milyon metre olarak düşünürsek bu durumda ışığın bir metre yol alması için geçen süre 1/300.000.000 saniye olacaktır. Bu sayede zaman boyutunu ışık hızı çarpı zaman biriminden ifade edebiliriz. Bu sayede de birbiri ile tutarlı üç koordinatımız olur.
Minkowski uzayı ve Öklid uzayı arasındaki fark nedir?
Bu koordinat sisteminde uzaysal boyutların hiçbirinde hareket etmeyen bir parçacık düz bir çizgi ile gösterilir. Çünkü sadece zamanda ileri doğru hareket ediyor olacaktır. Ancak zamanda hareket ederken uzamsal koordinatların en az birinde hareket ediyorsa grafikte çapraz bir çizgi ortaya çıkar. Hızlanma durumunda da eğri ile gösterilecektir.
Öklid geometrisinde iki nokta arasındaki mesafe bir değişmezi ifade eder. Koordinat sistemi değişse dahi yer değiştirme sabit kalır. Ayrıca bildiğimiz gibi mesafe her zaman pozitif olmalıdır. Üç boyutlu Öklid geometrisinde, bir noktanın merkeze olan r uzaklığı ise aşağıdaki bağlantıyı yazmamız olasıdır. İki boyutlu durumda ise bu ifade aslında hepimizin bildiği Pisagor teoremine dönüşecektir.
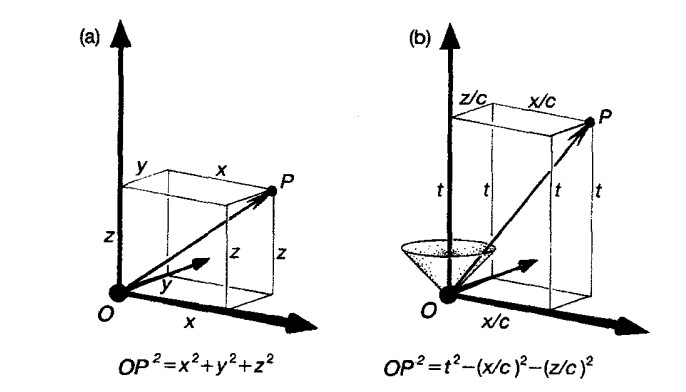
Minkowski geometrisinde de, esas olarak aynı şeyi kullanırız. Temelinde fark tek bir işarettir. Eksi işaretleri vektörel iç çarpım kuralları sonucunda ortaya çıkar. Ancak uzaklık bu durumda geçen zaman anlamındadır.
Şimdi bu koordinat düzleminin içinde bir ışık yaktığımızı düşünelim. Işık zamanla birlikte her yöne doğru yayılır. Bu da bir koni şeklini oluşturur. Minkowski buna ışık konisi adını vermişti. Uzay zamandaki herhangi bir A olayı için ışık konisi inşa edilebilir. Işığın A olayından sonra ulaştığı nokta gelecek olayları temsil eder. Alt kısımdaki koni ise A olayına ulaşan geçmiş olayları temsil etmektedir. Bu iki ışık konisinin dışındaki noktalar ise nedensel olarak A olayından kopuktur.
Sonuç olarak;
Bu yazımız sadece konuyu özetlemek adına yazılmıştır. Ancak sonuç olarak gördüğünüz gibi Minkowski uzayının ana yapısı, özel göreliliğin özünü içerir.
Kaynaklar ve İleri okumalar:
- Violating causality. Yayınlanma tarihi: 15 Ağustos 2017; Bağlantı: Violating causality
- Ask Ethan: What Is Spacetime? Yayınlanma tarihi: 28 Ocak 2017; Bağlantı: Ask Ethan: What Is Spacetime?/
- Pyragas, K. & Svirskas, Kestutis. (2005). On the Biography and the Scientific Heritage of Hermann Minkowski. Baltic Astronomy. 14. 323-330.
Matematiksel