Sokaktaki herhangi bir kişiye “kaç boyut var” diye sorduğunuz zaman, cevap büyük ihtimal ile üç olur. Oysa ki dünyanın en az dört boyutlu olduğunu biliyoruz. Ancak bilsek de hala bir çoğumuz bu dördüncü ve hatta beşinci boyutun ne olduğunu açıklayamıyoruz.

Dördüncü Boyut Nedir?
Sonucunda üç boyutlu bir dünyada yaşıyoruz. Yukarı ve aşağı, sağ ve sol, ileri ve geri. Birbirine dik açı yapan üç yöne sahibiz. Düz bir çizgi gibi tek boyutlu bir şeyi veya bir kağıda çizilmiş kare gibi iki boyutlu bir şeyi hayal etmek kolay. Ama 1905’te Albert Einstein, Özel Görelilik Teorisi’nde, uzayın, ışığın kozmik hız sınırı aracılığıyla zamanla yakından bağlantılı olduğunu ve dolayısıyla, kesin olarak konuşursak, uzay-zamanın dört boyutuna sahip bir Evrende yaşadığımızı gösterdi.
Bu nedenle artık Evreni uzayın üç boyutunda (kuzey-güney, doğu-batı, yukarı-aşağı) ve zamanın tek boyutunda (geçmiş-gelecek) düşünüyoruz. Zaman+uzay bir noktayı dört koordinatla (t, x, y, z) tanımlamamızı sağlar. Hatta 1920’lerde fizikçiler Oskar Klein ve Theodor Kaluza, Einstein’ın fikirlerinden esinlenerek, uzayın ekstra bir boyutu olarak beşinci boyutun var olabileceğini de ileri sürdü.

Daha yakın zamandaki gelişmeler bize aynı zamanda ek uzaysal boyutların da var olabileceğini gösterdi. Ve aslında fizikteki pek çok teori, boyutların sayısı konusunda kolaylıkla formüle edilebilir. Sonucunda (t, x, y, z….) biçiminde fazladan koordinatlar ekleyerek bu fazladan uzaylarda çalışmak mümkündür. Ancak tüm bu boyutları hala anlamak kolay değildir ve aslında bunun da basit bir nedeni vardır.
Dördüncü Boyutu Neden Anlayamıyoruz?
Film izlerken ekranda izlediklerimiz derinliğe sahip gibi görünse de görüntü aslında düzdür. Ancak 3 boyutlu gözlük taktığımızda içine girebileceğimiz bir dünya görürüz. Bu gördüklerimiz bize çok yabancı gelmez çünkü zaten böyle bir dünyada yaşıyoruz. Oysa ki yaşamı yalnızca iki boyutta bilen birinin üçüncü boyutu anlaması imkansızdır.
Birçok araştırmacıya göre dördüncü boyutu ya da onun ötesindeki herhangi bir boyutu göremememizin sebebi de budur. Fizikçiler en az 10 boyutun olduğu varsayımıyla çalışırlar, ancak çoğunluğumuz bunları asla “görmeyeceğiz”. Hayatı yalnızca 3 boyutlu olarak bildiğimiz için beynimiz daha fazlasını nasıl arayacağımızı anlamıyor.
1884 yılında, ek boyutlar kavramını açıklamak için, İngiliz matematikçi Edwin A. Abbott Flatland isimli bir roman yazdı. Romanın kurgusu içinde (çeşitli geometrik şekillerde) iki boyutlu varlıkların barındığı, iki boyutlu bir evrende geçmekteydi. Romanına da Düzülke adını vermişti. Abbott bize, bütün hayatlarını iki boyutta; örneğin bir masanın üstünde, yaşayan Düzülkelilerin, üç boyut fikrine, neden en az bizim dünyamızda yaşayan insanların, dört boyut fikrine şaşırdıkları kadar şaşırdıklarını anlatır.

Bizim için, üç boyuttan fazlası bir miktar hayal gücü gerektirir ama Düzülke’de, üç boyut orada yaşayanların algılarının ötesindedir. Çünkü evrenin, onların algılayabildiği iki boyuttan daha fazlasını barındırmadığı onlar için aşikardır. Düzülke’de yaşamak, kare biçiminde bir vatandaşın daireler, üçgenler ve dikdörtgenlerle çevrelendiği anlamına gelir. Ancak karenin gördüğü tek şey başka çizgilerdir.
Bir gün bir küre bu ülkeyi ziyarete gelir. Ancak kareye, bu küre bir daire gibi gözükür. Sonunda küre, kareyi 3 boyutlu dünyaya götürür ve kare içinden geçen nesnelerin kesitleri aracılığıyla durumu anlar. Sadece çizgileri değil, derinliği olan tüm şekilleri artık görmeye başlar. Aşağıda kitaptan bir çizimi görebilirsiniz.
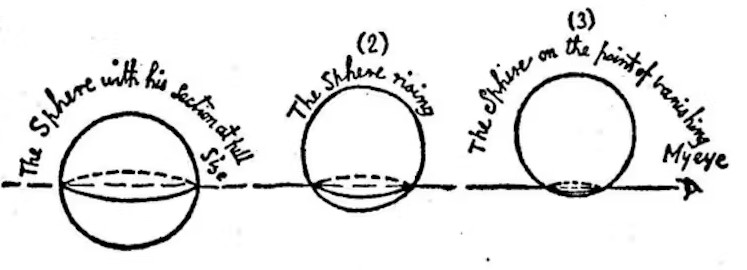
Ne yazık ki, dördüncü bir uzaysal boyutu, göstermeye çalışırsak, biz de aynı engellenmeye sahip oluruz. Ama bizim de henüz görmemiş olmamız, o boyutun orada olmadığı anlamına gelmemektedir.
Konu İle İlgili Bilimsel Çalışmalar Nasıl Başladı?
19. yüzyılın başlarında matematikçiler ve düşünürler, alıştığımız üç boyutun (derinlik, genişlik ve yükseklik) ötesinde dördüncü bir mekansal boyut fikrini keşfetmeye başladılar. August Ferdinand Möbius da bu ek boyutun olasılıkları üzerine kafa yoranlar arasındaydı. Daha sonra 19. yüzyılda matematikçi Bernhard Riemann, yüksek boyutlu uzayları anlamak ve onlarla çalışmak için matematiksel bir çerçeve sağlayarak gerçek dört boyutlu geometrinin temellerini attı.
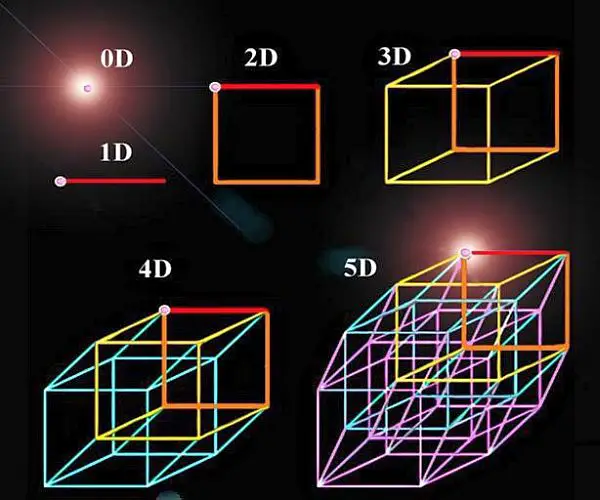
Hiperküp olarak da bilinen teserakt, 4 boyutlu uzayın yaygın bir görsel temsilidir. Küp (3 boyutlu nesne) kavramının dördüncü boyuta genişletilmesidir. Üç boyutlu dünyamızda görselleştirmek zor olsa da matematikçiler tesseract fikrini aktarmaya yardımcı olmak için diyagramlar ve modeller kullanır.
Dört boyutta bir hiperküpü ve beş boyutta daha isimlendirmemiş olduğumuz bir şeyi genelleyebiliriz. Bir hiperküp inşa edebilmek için bir küpü bir diğerinin üstüne koyun ve onları başlangıçtaki küpün yüzlerini kesiştirecek şekilde altı küp daha ekleyerek birleştirin. Bu yapı bir soyutlamadır ve çizimi zordur ama bu durum hiperküpü daha az gerçek yapmamaktadır.
Dördüncü Boyutu Anlamak Neden Önemlidir?

Zamanda yolculuk yapmak için kullanamıyorsak ve hatta göremiyorsak, o zaman onu bilmenin ne anlamı var? diye düşünmüş olmanız mümkündür. Oysa ki bu fazladan boyutları anlamak matematikçiler ve fizikçiler için önemlidir.
Günlük yaşamda navigasyon ve iletişim gibi görevler büyük ölçüde dördüncü boyut olarak zamanı kavramamıza bağlıdır. GPS ve doğru zaman tutma sistemleri gibi teknolojiler bu temel anlayışa dayanarak günlük yaşamlarımızı iyileştirir. Ayrıca Büyük Patlama, kozmik genişleme ve galaksilerin ve yıldızların oluşumu gibi önemli olayların incelenmesine yardımcı olarak kozmosa dair paha biçilmez bilgiler sağlar.

sanatçı Alexa Meade’nin çalışmaları buna bir örnektir.
Sonuç Olarak
Fiziksel teorileri görselleştirmedeki zorluklar hiçbir zaman onların reddedilmesi için geçerli bir temel oluşturamadı, ancak anlamanın önünde bir engel oluşturdular. Sonucunda sonsuzlukları ve kuantum mekaniksel durumların süper konumlarını hayal etmeyi de zor buluyoruz, ancak bu kavramların her ikisi de doğada görülüyor. Aynı durum dördüncü boyut için de geçerlidir. Tek sorun aslında algılarımızın sınırı ile ilgilidir.
Kaynaklar ve ileri İleri Okumalar:
- Understanding the Fourth Dimension From Our 3D Perspective. Yayınlanma tarihi: 4 Mayıs 2017. Kaynak site: Intersting Engineering. Bağlantı: Understanding the Fourth Dimension From Our 3D Perspective/
- How many dimensions are there? Yayınlanma tarihi: 28 ocak 2021; Kaynak site: ZME Scince. Bağlantı: How many dimensions are there?
- Our Universe may have a fifth dimension that would change everything we know about physics. Yayonlanma tarihi: 25 Temmuz 2023. Kaynak site: BBC Science Focus. Bağlantı. Our Universe may have a fifth dimension that would change everything we know about physics
- The 4th Dimension: Where Science and Imagination Collide. Yayınlanma tarihi: 20 Temmuz 2023. kaynak site: How Stuff Works. Bağlantı: The 4th Dimension: Where Science and Imagination Collide
- Understanding the hidden dimensions of modern physics through the arts. yyaınlanma tarihi: 28 Ekim 2015. Kaynak site: Conversation. Bağlantı: Understanding the hidden dimensions of modern physics through the arts
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










