Ünlü fizikçi Werner Heisenberg’e atfedilen bir rivayet, onun bir gün Tanrı’ya şu iki soruyu sormak istediğini anlatır: “Neden görelilik? Neden türbülans?” Bu alıntı kurgusal olsa da, türbülans hakkında kafa yoran pek çok fizikçinin hislerini yansıtır. Çünkü türbülans, bilim dünyasında çözülmesi en zor problemlerden biri olmaya devam ediyor.

Sıvılar ve havanın hareketi basit gibi görünebilir, ancak türbülans işin içine girdiğinde durum değişir. Örneğin, bir kasırganın bir masa tenisi topu fabrikasının çatısını uçurduğunu düşünün. Etrafa saçılan pinpon toplarının nereye düşeceğini tahmin etmek, karmaşık türbülanslı hava hareketleri nedeniyle neredeyse imkansızdır. Bu durum, fizikçiler ve matematikçiler için büyük bir zorluk yaratır.
Türbülans sadece doğal olaylarda değil, teknolojik tasarımlar ve süreçlerde de kendini gösterir. Uçakların aerodinamiğinden boru hatlarındaki sıvı akışına kadar birçok alan türbülansın etkisi altındadır. Hava durumu tahminleri gibi doğal olayların öngörülmesinde de türbülansın anlaşılması büyük önem taşır.

Türbülans, basitçe düzgün bir sıvı akışının küçük girdaplara ayrılmasıdır. Ancak bu girdaplar daha küçük girdaplara bölünür ve süreç devam ettikçe her bir girdap diğerlerini etkiler. Bu nedenle, bir sıvının herhangi bir noktasındaki hareketi kesin olarak tahmin etmek neredeyse imkansızdır.
Bu karmaşıklık, bilim insanları, mühendisler ve matematikçiler için sürekli bir meydan okuma oluşturur. Bunun nedeni, türbülansın farklı ölçeklerde ve ortamlarda meydana gelmesidir. Atmosferde binlerce kilometrelik mesafeleri etkileyebileceği gibi, okyanuslarda yüzlerce kilometrelik alanlarda hissedilir.

Laboratuvar ölçeğinde ya da jeofiziksel olaylarda türbülansı incelemek, her durumda farklı bir dinamikle karşılaşmayı gerektirir. İster astrofiziksel ölçekte, ister jeofizik ölçekte, ister laboratuvar ölçeğinde olsun, doğadaki çoğu akış türbülanslıdır. ( Fizik dilinde “akışkan”, sıvılar, gazlar ve hatta bazen kum gibi tanecikli malzemeler de dahil olmak üzere akan her şeydir. ) Bu akışları anlamak için bilim insanlarının elindeki tek araç matematiktir.
Türbülansın Matematiksel Temelleri Nelerdir?
Türbülans, sıvıların hareketini tanımlayan iki temel denklem setiyle açıklanır. Bunlardan biri, 18. yüzyıl matematikçisi Leonhard Euler’in geliştirdiği Euler Denklemleridir. Bu denklemler, viskoz olmayan sıvıların her anki hareketini ve hareketin basınçla ilişkisini tanımlar.
Euler denklemleri, sıvının hız ve basıncının hem zamana hem de uzaya göre değişim oranını açıklayan kısmi diferansiyel denklemlerdir. Ancak bu denklemleri gerçekçi koşullarda çözmek, 300 yılı aşkın süredir kimsenin başaramadığı bir zorluk olarak kalmıştır.
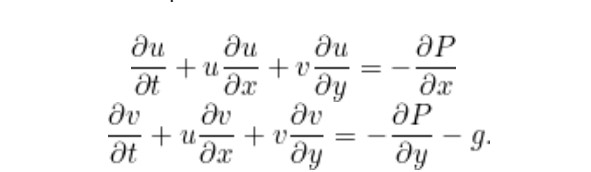
Euler denklemlerini çözmek, kısmi türevleri denklemleri karşılayan u, v ve P fonksiyonlarını bulmak anlamına gelir. Ancak aradan geçen 300 yıl içinde hiç kimse gerçekçi koşulları tanımlayacak denklemleri çözmeyi başaramamıştır.
Navier-Stokes Denklemleri Nedir?
Sıvıların hareketini tanımlayan bir diğer denklem seti ise Navier-Stokes denklemleridir. Bu denklemler, Euler denklemleriyle ilişkili olup, sıvıların viskozitesini (yapışkanlığını) de hesaba katar. Adını 19. yüzyıl matematikçileri Claude-Louis Navier ve Gabriel Stokes‘tan alan bu denklemler, bal ya da yağ gibi viskoz sıvıların hareketini açıklamada kritik bir rol oynar.
Navier-Stokes denklemleri, sıvının hızındaki değişiklikleri, basınçtaki değişikliklerle ve viskozite ile ilişkilendirir. Bu, sıvıların hareketini daha detaylı anlamamızı sağlar. Örneğin, su gibi düşük viskoziteli bir sıvı ile bal gibi yüksek viskoziteli bir sıvının hareket dinamikleri arasındaki farkı bu denklemlerle açıklamak mümkündür.
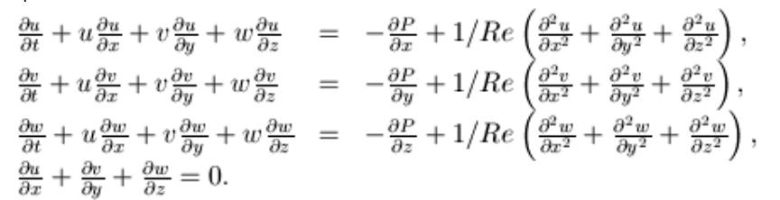
Bu denklemler, Newton’un İkinci Hareket Yasası‘nın bir akışkana uygulanmış halidir. 200 yılı aşkın bir süredir yapılan deneyler, bu denklemlerin inanılmaz derecede faydalı olduğunu göstermiştir. Navier-Stokes’un öngördüğü akış davranışları, gerçek dünyada gözlemlenen akışlarla büyük ölçüde uyumludur. Ancak, bu denklemleri çözmek bilim insanları ve mühendisler için hala büyük bir zorluktur.
Uygulamada, Navier-Stokes denklemleri birçok sıvı akışı için neredeyse mükemmel çözümler sunar. Ancak bu çözümler genellikle yaklaşık çözümlerdir. Yani, denklemlerin kesin çözümleri değildir. Bu yaklaşık çözümler, mühendislikten meteorolojiye kadar birçok alanda güvenle kullanılsa da, denklemlerin varlığı ve çözümlerinin sınırları hakkında resmi bir matematiksel kanıt bulunmamaktadır.
Bu nedenle Clay Matematik Enstitüsü‘nün 2000 yılında ortaya koyduğu yedi matematik problemi arasında Navier-Stokes denklemleri de vardır. Bu problemler, matematik dünyasının en büyük meydan okumaları arasında yer alır ve her biri için 1 milyon dolarlık bir ödül vaat edilmiştir.
Aslında Clay Enstitüsü’nün ödülü vermek için talep ettiği bilgi ise oldukça basittir. Birincisi denklemlerin çözümlerinin varlığına odaklanır. İkincisi ise bu çözümlerin sınırlı olup olmadığını (sonlu kalıp kalmadığını) sorar.
Reynolds Sayısı: Akışkanların Sınıflandırılması
Belirli bir sıvı akışını ele aldığınızda, Euler veya Navier-Stokes denklemlerinin çözümleri, sıvının zaman ve uzayda herhangi bir noktadaki hızını ve basıncını size söyler. Bu kulağa her şeyi tahmin edebileceğimiz bir dünya sunuyormuş gibi gelecektir. Ancak bu denklemler doğrusal değildir ve bu doğrusal olmama durumu, işleri oldukça karmaşık hale getirir.
Eğer denklemler doğrusal olsaydı, tüm akışkanların davranışlarını her zaman ve her yerde kesinlikle tahmin edebilirdik. Ancak bu, gerçek dünyada mümkün değildir. Bunun yerine, Hesaplamalı Akışkanlar Dinamiği (Computational Fluid Dynamics – CFD) kullanılarak, denklemlerimizin doğruya yakın yaklaşık çözümleri elde edilir.

Ancak bu süreç, büyük bilgi işlem gücü gerektirir. Süper bilgisayarlar olmadan bu tür hesaplamaları yapmak oldukça zordur, çünkü türbülansın karmaşıklığı ve ölçekleri hesaplamalar sırasında büyük miktarda veri üretir.
Akışkanları ve onların hareketlerini daha iyi anlamak için, bilim insanları Reynolds sayısı adı verilen bir ölçüt kullanır. Reynolds sayısı, bir akışkanın hızı ile viskozitesi (yapışkanlığı) arasındaki ilişkiyi temsil eder. Bu sayı, akışkanların davranışını sınıflandırmamıza yardımcı olur:
- Düşük Reynolds Sayısı: Akışkanın hareketi genelde düzenlidir ve türbülans görülmez. Örneğin, bal gibi viskoz sıvılar bu kategoriye girer.
- Yüksek Reynolds Sayısı: Akışkanın hareketi karmaşıktır ve türbülanslıdır. Hızlı hareket eden nehirler ya da atmosferik hava akımları buna örnek olarak gösterilebilir.
Reynolds sayısı, akışın düz (laminer) veya türbülanslı olup olmayacağını anlamamızda kilit bir rol oynar. Ancak, Reynolds sayısını bilmek bile türbülansın kaotik doğasını tam anlamıyla çözmemizi sağlamaz.
Sonuç olarak
Türbülans, hayatımızın birçok alanında etkili olan karmaşık bir olgudur. Gözlemlenmesi kolay gibi görünse de, bilimsel olarak modellenmesi ve anlaşılması son derece zordur. Türbülansın temelini anlamak için matematik, fizik ve mühendislik disiplinlerinin iş birliği içinde çalışması gereklidir.
Kaynaklar ve ileri okumalar
- Why turbulence is troubling. Yayınlanma tarihi: 22 Nisan 2022. Kaynak site: PlusMath. Bağlantı: Why turbulence is troubling
- Turbulence trouble. Yayınlanma tarihi: 3 Şubat 2021. Kaynak site: Cosmos. Bağlantı: Turbulence trouble
- Turbulence, the oldest unsolved problem in physics. Yayınlanma tarihi: 10 Ekim 2018. Bağlantı: Turbulence, the oldest unsolved problem in physics
Matematiksel