Zeno paradokslarından en çok bilinen 4 tanesi, hareket konusunu ele alır. Bu paradokslar, hareketin gerçek gibi görünse de gerçekte var olmadığını göstermeyi amaçlar.

Sokrates öncesi düşünürlerin en önemlilerinden sayılan Parmenides, felsefe tarihinde 5. yüzyılın ilk yarısında etkin olmuştur. Kendisi ayrıca doğduğu kent Elea’da aynı adı taşıyan bir felsefe okulu kurmuştur. Felsefe tarihinde bu okulun üyelerine Elealılar denir. Evrenin kendisini oluşturan atomlara bölünebileceğine inanan çoğulcuların aksine, Elea felsefesi her şeyin bölünmezliğine inanır. Ayrıca görünüş ile gerçeklik arasında bir ayrım olduğunuz savunurlar.
Elealı Zeno (MÖ 490- 430) da Parmenides’in öğrencisi ve aynı zamanda Parmenides’in manevi oğludur. Bir mantık ustası ve diyalektik düşüncenin en önemli geliştiricilerinden biridir. Felsefe tarihinde Zeno paradoksları olarak anılan paradoksları Parmenides’in öğretisini desteklemek amacıyla yaratmıştır. Çalışmalarından hiçbiri günümüze ulaşmamış olsa da, 40’tan fazla paradoks ona atfedilir.
Parmenides, gerçekliğin tek, sabit, değişmez bir şey olduğuna ve “Varlık” adını verdiği tekliğe inanıyordu. Bu radikal inancı savunurken Zeno, değişimin yani hareketin imkansız olduğunu göstermek için 40 argüman oluşturmuştu.
Akhilleus ile Kaplumbağa Paradoksu
Birçok bilim dalının temelini oluşturmuş matematik bilimi, fizik bilimi ile de bir hayli içli dışlıdır. Ancak matematiksel bazı ifadeler fiziksel bazı ifadelerle bazen ters düşer. Bunlardan birisi de sonsuzluk kavramıdır.
Zeno paradokslarından en çok bilinen 4 tanesi, hareket konusunu ele alır. Bu paradokslar, hareketin gerçek gibi görünse de gerçekte var olmadığını göstermeyi amaçlıyordu. Bu paradoksların en ünlüsü Yunan kahraman Akhilleus’un adıyla anılan “Akhilleus ile Kaplumbağa Paradoksu” dur. Biz daha kolay anlaşılabilen ilk üç paradoksu yazımızda ele alacağız.

Yunan kahramanı Akhilleus ( Aşil) bir kaplumbağa ile yarış yapmaktadır. Kaplumbağadan 10 kat daha hızlı olan Aşil, rakibine bir yarışta 10 metre önde başlama şansı verir. Eğer her ikisinin de sabit hızlarda koştuğunu düşünürsek belirli bir süre sonra Aşil on metre koştuğunda, kaplumbağanın başladığı yere gelmiş olacaktır. Bu süre boyunca kaplumbağa da küçük de olsa belirli bir mesafe koşmuştur.
Yani 1 metre. Aşil bir süre sonra bu mesafeyi de tamamladığında, o süre zarfında kaplumbağa yine küçük de olsa bir mesafe ilerlemiş olacaktır ve bu böyle devam edecektir. Böylece, Aşil ne zaman kaplumbağanın varmış olduğu bir noktaya varsa, daha hâlâ gitmesi gereken bir mesafe kalmış olacaktır. Bu nedenle Zeno, Aşil’in kaplumbağayı hiçbir zaman geçemeyeceğini söyler.
Matematiksel Açıdan Sorun Nerede?
Matematiksel anlamda düşündüğümüzde bu düşünce elbette hatalıdır. Sonuçta Aşil, kaplumbağanın başladığı noktaya ulaştığında (T0 = 10 m), yavaş ama istikrarlı kaplumbağa 1 metre ilerlemiş yani T1 = 11 m’ye hareket etmiş olacaktır.
Aşil T1‘e ulaştığında, kaplumbağa 0.1 metre ilerleyecektir. (T2 = 11.1 m’ye). Sonuçta her ikisi de 11 m’nin biraz üzerinde koştuğunda Aşil’in kaplumbağayı 1.11 saniye sonra geçmesi gerektiğini biliyoruz. Bu yüzden Aşil aslında 11.11 metreden daha uzun herhangi bir yarışı kazanacaktır. Ama neden Zeno’nun argümanında kendisi kaplumbağayı asla yakalayamayacak gibi görünüyor dersiniz?

Aslında Aşil’in aldığı yolu bir geometrik seri biçiminde gösterebiliriz. 10 + 1 + 0.1 + …. + 10(2-n) + …. Bu geometrik serinin çarpanı birden küçüktür. Bu nedenle mesafenin sonlu olduğunu biliyoruz. Yani Aşil sabit bir hızla, sınırlı bir mesafe seyahat ediyorsa bu mesafeyi sonlu bir zamanda kat edecektir. Yani matematik açısından, Aşil ve kaplumbağa hakkında gerçekte hiçbir paradoks yoktur.
Ancak Zeno’nun argümanı, uzayı (yarış pisti) ve zamanı (koşmanın ne kadar sürdüğü) sonsuz olarak bölebileceğiniz varsayımına dayanmaktadır. Bu sayede yarışı sanki hiç bitmeyecekmiş gibi görünen sonsuz sayıda adıma dönüştürür.
Uzayı ve dolayısıyla zamanı daha küçük parçalara bölerek zamanın geçişinin ‘yavaşladığını’ ima eder. Ancak zamanın bu şekilde yavaşlamadığını biliyoruz. Uzayın (ve zamanın) sonsuz bölünebilir olduğu varsayımı yanlıştır.
Dikotomi Paradoksu
Zeno bu paradoksta bir koşucunun düz bir yarış pistinde sabit hedef çizgisine asla ulaşamayacağını söyler. Sonuçta koşucunun önce hedefe kadar olan mesafenin yarısına ulaşması gerekir. Oraya vardıktan sonra da kalan mesafenin yarına varmalıdır, sonra da yine kalanın yarısına.
Yani hedef bir metre uzaktaysa, koşucu 1/2 metre, sonra 1/4 metre, sonra 1/8 metre biçiminde yol almalıdır. Bu durumda hedefe ulaşması asla mümkün değildir.
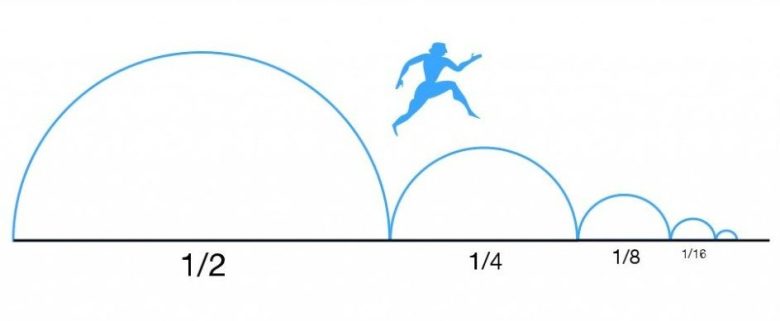
Koşucunun hedefe ulaşması sorununa farklı bir açıdan bakalım. Paradoksun bir diğer versiyonuna göre, koşucu ilk adımı bile atamaz. Herhangi bir adım kavramsal olarak ilk yarı ve ikinci yarıya bölünebilir. Koşucu tam bir adım atmadan önce 1/2 adım atmalıdır, ancak ondan önce 1/4 adım atmalıdır, ancak ondan önce 1/8 adım ve sonsuza kadar böyle devam eder. Bu nedenle koşucu asla koşamaz.
Aşil Paradoksu gibi, bu paradoks da herhangi bir hareketin imkansız olduğu sonucuna varır. Bu sonuç size saçma gelebilir. Ancak bu Zeno’nun problemlere yaklaşım biçimiydi. Her iki paradoksta da Zeno, uzay ve zamanın sürekliliğini varsaydı ve sonra bu varsayımdan bir çelişki çıkardı. Bu nedenle de, süreklilik varsayımının yanlış olduğunu kabul etti..
Ok Paradoksu
Zeno’nun Ok Paradoksu, zaman ve hareket kavramlarımızın tutarlılığına meydan okumak için farklı bir yaklaşım benimser. Yalnızca bir anlık görüntüsüne baktığınız takdirde, uzayda sabit duran bir oku uzayda hareket eden bir oktan ayırmanız mümkün olur muydu?
Yaydan fırlamış ilerlemekte olan bir ok düşünelim. Ok zaman içindeki her anda belirli bir konumda olacaktır. An denilen şey belirli, tek bir noktaysa, okun o anda hareket etme zamanı olmayacaktır, yani durağan olacaktır. Dolayısıyla gelecek anlarda da durağan olacaktır. Bu şekilde her an durağan olacaktır ve hareket etmeyecektir.
Aslında, uzay ve zamanın ayrı olduğu bir dünyada, uçan bir ok Zeno’nun dediği gibi davranırdı. Ancak Zeno, böyle bir dünyada hareketin imkansız olacağı konusunda yanılıyordu. Bunu hepimiz dijital cihazlarımızda film ve video izleme deneyimimizden biliyoruz.
Cep telefonlarımız ve bilgisayar ekranlarımız her şeyi ayrı piksellere bölüyor ve yine de Zeno’nun iddiasının aksine, bu ayrık manzaralarda hareket mükemmel bir şekilde gerçekleşebiliyor. Eğer uçuş halindeki bir okun yüksek çözünürlüklü videosunu izleseydik, aslında birbiri ardına ayrı karelerde cisimleşen bir ok görüyor olurduk. Ancak Zeno bunu elbette bilemezdi.
Zeno’nun uzay, zaman ve hareket hakkında kaleme aldığı, sonsuzluğun baş döndürücü ve şaşırtıcı bir rol oynadığı bu paradokslar günümüzde hala bilim dünyasında tartışılmaya devam ediliyor. Argümanları, Platon ve Aristoteles aracılığıyla bize ulaştı.
Anlattıklarında Zeno, değişimin imkansız olduğunu kanıtlamaya çalışıyordu. Duyularımız bize aksini söylese de Zeno’ya göre değişim bir yanılsamaydı. Neyse ki matematik sayesinde duyularımıza güvenmek zorunda kalmadan cevaplar bulabiliyoruz.
Kaynaklar ve İleri Okumalar:
- Zeno’s Paradoxes Verses Reality; yayınlanma tarihi: 7 Kasım 2019; Bağlantı: https://www.ancient-origins.net/
- Mathematical mysteries: Zeno’s Paradoxes; Yayınlanma tarihi: 1 Aralık 2000; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










