Bir probleminin çözümünü hesaplamak yerine hayal etmeyi denediniz mi? Bazı konularda araştırma yapmak mümkün değildir. Bu durumlarda işin içine kişinin hayal gücü ve düşünce deneyleri girer. Düşünce deneyleri, karmaşık veya soyut fikirleri anlamak, mantıklı sonuçlara varmak veya bir görüşü test etmek amacıyla kullanılır.
Düşünce deneyleri farklı formlarda karşımıza çıkar. Örneğin, “Trolley Problem” (Tramvay İkilemi) gibi bir düşünce deneyi, etik konuları ele alırken kullanılırken, “Zeno’s Paradoxes” (Zenon Paradoksları) gibi deneyler matematiksel ve fiziksel kavramları keşfetmek için kullanılır. Bu yazıda sizlere modern zaman ait dört düşünce deneyinden bahsedeceğiz.
Einstein’ın Tren Deneyi
Modern zamana ait düşünce deneylerinden bahsettiğimiz zamanlarda akla gelen ilk isim elbette Einstein olacaktır. Einstein bu düşünce deneyini 19. yüzyılın sonlarına doğru, aynı anda iki olayın gözlemciler tarafından farklı zamanlarda algılanabileceği fikrini açıklamak amacıyla kullanılmıştır.
Bu düşünce deneyinden önce insanlar zamanın tüm referans çerçevelerinde evrensel olarak sabit olduğunu kabul ediyorlardı. Ancak Einstein, bir çerçeve diğerine göre hareket ediyorsa, olayların farklı fiziksel referans çerçevelerinde eşzamanlı olmadığını gösterdi. Başka bir deyişle, zaman aslında göreceliydi.
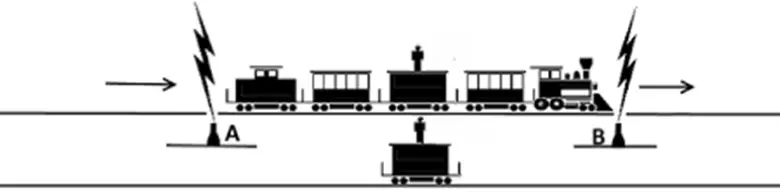
Bir trenin geçişini izleyen bir gözlemci olduğunuzu düşünün. Trenin tam ortasında da bir arkadaşınız olsun. Arkadaşınız ile siz aynı hizaya geldiğiniz anda trenin her iki ucuna da yıldırım düşsün. Bu yıldırımların her ikisini de siz aynı anda göreceksiniz.

Ancak aynı durum trenin ortasındaki kişi için geçerli olmayacaktır. Yukarıdaki diyagramda, yıldırım çarpmaları A ve B noktalarında meydana gelmektedir. A ve B noktalarından gelen iki ışık huzmesi M orta noktasında buluşmaktadır. Bu sırada trende bir yolcu, M’ noktasında bulunduğu ve sağa doğru gittiği için birinin diğerinden çok az önce parladığını görecektir. Yani A noktasından gelen parlamayı görmeden önce B noktasındakini görecektir. Bu da, onun B noktasındaki yıldırımın önce gerçekleştiğini düşünmesine neden olacaktır.
Bu düşünce deneyine dayanarak Einstein, zamanın kişinin hangi referans çerçevesine sahip olduğuna bağlı olarak değiştiği sonucuna vardı. Bu nedenle de bu düşünce deneyi, Einstein’ın izafiyet teorisinin temel taşı niteliğindedir.
İkizler Paradoksu

Einstein’ın özel görelilik teorisi bize zamanın göreceli olduğunu öğretir. Fakat zamanın göreceli olması ne anlama geliyor? Olayların ne zaman başladığı, ne zaman bittiği ve ne kadar sürdüğü konusunda kimsenin hemfikir olmadığı bir evrende nasıl yaşayabiliriz? İkizler paradoksu bu soruya cevap vermeyi amaçlıyor.
Einstein 1905 tarihli makalesinde izafiyet teorisi hakkında yazdığında, bir problemi merak ediyordu. Neyse ki Einstein koltuğundan kıpırdamadan deney yapmakta oldukça başarılıydı. Bu problemin cevabını da başka bir düşünce deneyi ile bulacaktı.
Basitçe söylemek gerekirse, özel görelilik, hareket eden bir nesneye bağlı bir saatin, duran bir nesneye bağlı olana göre daha yavaş çalışacağını söyler. Bu durumu kolumuzdaki saate bakarak anlamamız zordur. Sorun ışık hızına yaklaştığımız zamanlar da ortaya çıkacaktır.
Bu fikrin tüm sonuçlarını keşfetmek için, düşünce deneyine ikizler kardeşler Alice ve Bob ile başlayalım. Birbirlerine yakın durdukları sürece saatleri senkronize kalacak ve aynı oranda yaşlanacaklardır. Ama Bob bir uzay gemisine binip galakside ışık hızına yakın bir hızla dolaşsaydı, her şey biraz farklı olurdu.
Bob için yolculuğunda belki sadece birkaç ay veya birkaç yıl geçerdi. Bu esnada zamanın geçişini de tamamen normal hissederdi. Ama ne kadar hızlı gittiğine bağlı olarak Alice için on yıllar, hatta yüzyıllar geçmiş olabilirdi.
Bu hikaye ne kadar kafa karıştırıcı olsa da, bu bir paradoks değildir. Bu, Einstein’ın özel göreliliği geliştirmesine yardımcı olan çok önemli düşünce deneyidir. Zaman genişlemesi olarak bilinen zamanın yavaşlaması, birçok deneyle doğrulanmıştır. Ancak bunun neden olduğunu konusunda henüz tek bir anlaşma yoktur. Yakın zamanda yayınlanan bu çalışma paradoksun henüz çözülmediğini doğrulamaktadır.
Çin Odası Düşünce Deneyi

“Çin Odası Argümanı” olarak da bilinen bu ilgi çekici düşünce deneyi, bilgisayarların insan dilini anlamadan onu nasıl taklit edebildiğini ele alır. Yapay genel zeka dediğimiz zamanlar da yeni görevleri hızla öğrenebilen ve yeni sorunları esnek bir şekilde çözebilen bir üst sınıftan bahsederiz. Peki yapay genel zekanın var olması mümkün mü?
Filozof John Searle, Minds, Brains ve Science (1984) adlı kitabında bir yapay zekanın insanlar tarafından yapılan zihinsel süreçleri taklit edeceğini, ancak bu esnada ne yaptığının farkında olmayacağını savundu. Amacını daha iyi açıklamak için de Çin Odası deneyini tasarladı.
Tek kelime Çince bilmeyen bir Türk’ü bir odaya kapattığımızı düşünelim. Bu esnada da eline, bir dizi Çince karaktere başka bir karakter dizisiyle nasıl yanıt vereceğini söyleyen, Türkçe yazılmış bir kılavuz kurallar kitabı verelim. Odanın dışından birileri, kapının altından üzerinde Çince karakterler ile yazılı sorular olan kağıtlar atsın.
İçerideki adam da “Şu harfler gelirse şu harfleri yaz” türünden talimatlara bakarak bu sorulara cevap versin. Sonrasında da bu cevapları kapının ardından geri yollasın. Sonucunda bu görev bu adam için anlamsızdır. Gelgelelim farkına varmaksızın tek kelime Çince bilmeden Çince konuşan birini taklit etmiş olacaktır. Bu durumda dışardaki kişilerin içerde bir Çinli’nin olduğuna ikna olması da olasıdır.
Searle’e göre bilgisayarlar sembolleri insan düşüncesini simüle edecek şekilde işlerler. Ancak aslında akılsız otomatlardır. Bütün yaptıkları, onları oluşturanların kendilerine programlamış oldukları kurallar çerçevesinde sembolleri dağıtmaktır. Bu düşünce deneyi, “Turing Testi“nin gerçek yapay zekaya dair kanıt sağlamadığını ileri sürer.
Mary’nin Odası (Bilgi Argümanı) Düşünce Deneyi

20. yüzyılın önemli filozoflarından biri olan Frank Cameron Jackson, özellikle bilinç ve fizikalizm alanlarındaki çalışmalarıyla tanınmıştır. Jackson’in en ünlü çalışmalarından biri, “What Mary Didn’t Know? isimli makalesinden gelir. Jackson, bu makalesinde, Mary adında bir karakteri ele alarak ünlü “Mary’nin Odası” düşünce deneyini tasarlar.
Mary adında son derece zeki ve hayatını bilime adamış bunun neticesinde de son derece başarılı bir nörolog olmayı başarmış bir kadın düşünün. Uzmanlığı renkler ve renkli görüş üzerine olsun. Renk fizyolojisi ve biyolojisi ile alakalı keşfedilen her bilgiden haberdar. Yani bilgisi konusunda yok yok. Ancak Mary’nin bir sorunu var.
Mary tüm hayatını siyah-beyaz bir odada geçirmiş. Çevresindeki odada gördüğü her şey, yemeği, televizyonu, kitapları, bilgisayar ekranı siyah, beyaz veya gri tonlarında. Yani Mary, tüm hayatı boyunca hiç bir renk görmemiş. Mary, siyah beyaz odasından bir gün çıkar. Çıkar çıkmaz da, diğer odanın masasında duran, parlak kırmızı bir elma ile karşılaşır. Bu sayede artık kırmızı görmenin nasıl bir şey olduğunu öğrenir.
Filozoflar bu deneyi “Bilgi Argümanı” olarak adlandırırlar. Frank Jackson’a göre renk tecrübesi gibi bazı şeyler fiziksel olarak aktarılamaz. Fiziksel gerçekler sevgi, can sıkıntısı, endişe gibi zihinsel süreçleri açıklayamaz.
Bu argüman evrenle ilgili yalnızca fiziksel gerçeklerden daha fazlasının bilinip bilinmeyeceğine odaklanır. Bir kişi, yalnızca fiziksel gerçekleri biliyorsa, bilgisinin önemli bir şekilde sınırlı olduğunu iddia eder. Bu nedenle de günümüzde en çok tartışılan argümanların başında yer alır.
Kaynaklar ve ileri okumalar
- 4 Thought Experiments That Ask Tough Questions About the Nature of Reality. Bağlantı: 4 Thought Experiments That Ask Tough Questions About the Nature of Reality
- Einstein’s Relativity Explained in 4 Simple Steps. Yayınlanma tarihi: 16 Mayıs 2017. Bağlantı: Einstein’s Relativity Explained in 4 Simple Steps
- The ‘twin paradox’ shows us what it really means for time to be relative. Yayınlanma tarihi: 17 Mayıs 2022. Bağlantı: The ‘twin paradox’ shows us what it really means for time to be relative
- Mohazzabi, Pirooz & Luo, Qinghua. (2021). Has the Twin Paradox Really Been Resolved?. Journal of Applied Mathematics and Physics. 09. 2187-2192. 10.4236/jamp.2021.99138.
Matematiksel