Matematik çoğu zaman kalıpların incelenmesi ile ilgilidir ve karşımıza bir kalıp çıktığı zaman da insanlar bunda bir gizem olduğuna kolayca ikna olurlar. Buna bir örnek altın oran ve onunla bir biçimde ilişkili olan Fibonacci dizisidir.
Altın oranın tarihi hakkında bir sürü hikaye vardır. Bu hikayeler sizlere Mısır piramitlerinin, Yunan tapınaklarının, Mona Lisa portresinin altın orana uyacak şekilde yapıldığını söyleyecektir. Mistik öğeler barındırdığı için tüm bu hikayeler ilgi çekicidir ancak hatalıdır. Aynı biçimde Fibonacci dizisi ile ilgili de duyduğunuz bir çok şey yanlıştır. Altın oran miti ile ilgili yazımızı buradan inceleyebilirsiniz: Altın Oran Nedir? Hakkında Duyduklarımıza İnanmalı mıyız?

Fibonacci Dizisi Nedir?
Fibonacci dizisi, her sayının kendisinden önceki iki sayının toplamı olduğu bir sayı dizisidir. 0 ve 1’den başlayarak, dizinin ilk 10 sayısı şöyle görünür: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ve sonsuza kadar böyle devam eder. Matematiksel bir denklem olarak ifade etmemiz gerekirse bu dizi Xn+2= Xn+1 + Xn biçiminde yazılacaktır.

Bu dizi adını İtalyan Leonardo Bigollo Pisano’dan alır. (1170 – 1250). Kendisi Orta Çağ’ın en yetenekli Batılı matematikçisi olarak kabul edilmektedir. Ancak biz kendisini daha çok ‘Fibonacci’ lakabıyla, yani ‘Bonaccio’nun oğlu’ olarak biliriz.
Fibonacci ismi 18. yüzyıldan önceki kayıtlarda yer almamaktadır. Bu lakabın daha sonraları Guillaume Libri tarafından adına eklendiği düşünülmektedir. Ancak onun adı ile günümüzde anılsa da, bilinmesi gereken ilk şey, dizinin aslen Fibonacci’ye ait olmadığıdır.

Tarihe baktığımızda, Gopala (1135) ve Hemanchandra (1150) gibi birçok Hintli matematikçinin aslında söz konusu sayı dizisine atıflar yaptığı göze çarpmaktadır. Ancak Fibonacci’nin Liber Abaci’yi yazdığı dönemde bu sayılar özel bir şey olarak tanımlanmamıştı.
Fibonacci’nin matematiğin gelişimine katkısı büyüktür. Babasıyla yaptığı yolculuklar sonucunda tanıştığı Hindu-Arap matematiğinden son derece etkilenmiş ve bunun sonucunda 1202’de Liber Abaci adlı kitabı kaleme almıştır. Kitap, Hint-Arap sembollerini Avrupa’ya tanıtması anlamında önemlidir.
Fibonacci Dizisi ve Tavşan Problemi

Bu kitabın üçüncü bölümünde, bir problem yer alır. ‘Adamın biri, her tarafı duvarla çevrili bir yere yeni doğmuş bir dişi ve bir erkek tavşan koyar. Tavşanlar bir aylıkken çiftleşebilir, böylece ikinci ayın sonunda dişi tavşanımızın iki tavşan yavrusu daha olur. Bu tavşanlar ayda bir kez bir çift tavşan yavrularsa ve bu yavrular da ikinci aydan itibaren yavrulamaya başlarsa, adamın bir yılda kaç çift tavşanı olur? İşte bu problem bizi tarihe adını Fibonacci dizisi olarak yazacak bir sayı dizisi ile tanıştırır.
Şöyle düşünün. İlk ayın sonunda çiftleşirler, ancak hala sadece 1 çift vardır. İkinci ayın sonunda dişi yeni bir çift doğurur, yani şimdi 2 çift tavşan vardır. Üçüncü ayın sonunda, orijinal dişi ikinci bir çift daha doğurur ve toplamda 3 çift yapar.
Dördüncü ayın sonunda, orijinal dişi yeni bir çift daha doğurur ve bu esnada iki ay önce doğan dişi de ilk çiftini doğurur ve toplamda 5 çift yapar. Bu problemde tavşanlar hiç ölmez. Bunun sonucunda mantığı devam ettirirseniz bir yıl sonunda 233 çift tavşan olacağını göreceksiniz.
Yukarıdaki problem kitapta yer alsa da Fibonacci, kitabının başka bir yerinde bu diziden bir daha bahsetmez. Kimsenin de fazla ilgisini çekmez. Nitekim ünlü Alman matematikçi ve astronom Johannes Kepler (1571-1630), 1611 tarihli “Strena Seu de Nive Sexangula” adlı eserinde bu sayı dizisini incelemiştir. Ancak bu sayılar matematikçiler arasında yine de fazla ilgi görmemiştir.
Fibonacci Dizisinden Altın Orana Geçiş
Fibonacci sayıları ancak 1800’lerin ortalarında matematikçilerin ilgisini çekmeye başlayacaktı. 1877’de Fransız matematikçi Édouard Lucas, tavşan problemini resmen “Fibonacci dizisi” olarak adlandırdı. Matematiği popülerleştirme çabasında olan ve sayılar ile oynamayı seven Édouard Anatole Lucas, bu sayılarda küçük bir değişiklik yaparak Lucas sayılarını da ortaya attı.

Bu sıralarda Fransız matematikçi Jacques-Philippe-Marie Binet (1786-1856), konumu verilen herhangi bir Fibonacci sayısını bulmak için bir formül geliştirdi.
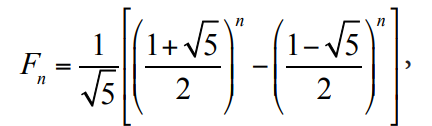
1753’te de Robert Simson, ardışık Fibonacci sayıları arasındaki oranın bir sayıya yaklaştığını fark etti. Bu sayede de Fibonacci dizisi matematikçilerin ilgisini daha fazla çekmeye başladı. Sonuçta altın oran ile ilişkisi ortaya konulmuştu. Fibonacci sayı dizisi, Fibonacci’ye matematikçilerin nezdinde ölümsüzlük verilmesine yetti. Bu sayede altın oran efsanesi ile Fibonacci sayı dizisi birleşmiş oldu.
Fibonacci Dizisi Doğada Karşımıza Çıkar mı?
Bu sayılar günümüzde genelde tavşanlar ile ilişkilendirilse de aslında Leonardo Fibonacci, hiç bir zaman biyoloji ile ilgilenmek gibi bir amaca sahip olmamıştı. Verdiği tavşanlar sadece bir örnekti. Gerçek tavşanlar, Fibonacci’nin varsaydığı gibi üremezler. Ancak Fibonacci dizisi, arıların üreme şemasını açıklar.
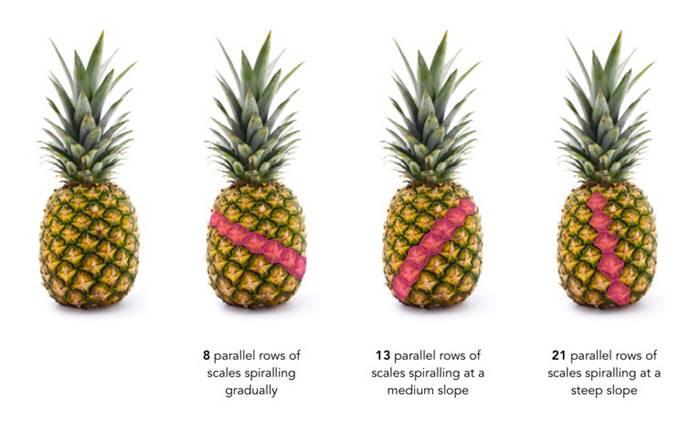
Arılar tek istisna da değil. Fibonacci sayıları bitkilerde ve çiçeklerde de görülür. Bazı bitkiler, her zaman bir Fibonacci sayıda büyüme noktasına sahip olacak şekilde dallanır. Bir ananası veya bir çam kozalağını inceleyin. Bu bitkilerde, yukarıdan aşağıya doğru uzanan spiral biçiminde pul sıraları vardır. Spiral sıralarının sayısı ananasta genellikle 8 ve 13’tür. Çam kozalağında ise tipik olarak 13 ve 21 veya 21 ve 34 biçimindedir.
Ayçiçeğinde ise çiçeğin ortasından dışarıya doğru genişleyen spiraller bulacaksınız. Bu spirallerin toplam sayısı genellikle saat yönünde ve saat yönünün tersinde sırasıyla 34 ve 55 veya 55 ve 89 olacaktır. Aynı şekilde çiçeklerde taç yaprakları sayarsanız 8,13, 21, 34 ve 55 gibi sayıların diğerlerinden daha yaygın olduğunu görürsünüz.

Gördüğünüz gibi Fibonacci dizisi doğada birkaç yerde kendini gösterir. Ancak bu evrenin mimarisini yöneten bazı gizli kodlar olduğu anlamına gelmez. Doğada bazı sayıların diğerlerinden daha sık görünmesi tahmin ettiğiniz gibi tesadüf eseri değildir. Bitkiler güneşe ve besine erişebilmek için belli bir biçimde gelişmek zorundadır. Bu dizilim de bunun bir sonucudur. Detaylar için: Dört Yapraklı Yonca, Altı Yapraklı Çiçek Neden Nadirdir? Cevap Fibonacci Sayıları Olabilir
Kaynaklar ve ileri okumalar:
- Fibonacci and his Magic Numbers; https://www.bbvaopenmind.com/
- What is the Fibonacci sequence? Yayınlanma tarihi: 1 Mart 2023; Bağlantı: https://www.livescience.com/
- Maths in a minute: the Fibonacci sequence; yayınlanma tarihi: 1 Mayıs 2020; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel