Asal sayılar ile ilgili yenir bir gelişme haberi duyurulduğu zaman, çoğu kişinin kafasında klişe bir cümle olan “iyi de bu benim ne işime yarayacak?” ister istemez oluşmaktadır. Aslına bakarsanız bir zamanlar, asal sayılarla ilgili keşifler pek de işe yaramamaktaydı. Ancak internetin hayatımıza dahil olduğu zamanlardan itibaren bu durum tamamen değişti.
Günümüzde internetle iletişime girdiğimiz hemen her noktada asal sayıların bize sağladığı güvenlik sayesinde içimiz rahat bir biçimde işlemlerimize devam ediyoruz. Kısacası asal sayılar şifreleme yani kriptografinin de temelini oluşturuyor.
Asal sayılar, genellikle sayıları oluşturan atomlar olarak adlandırılmaktadır. Bunun nedeni asal çarpanlara ayırma ile ilgilidir. Örneğin, 10 sayısı iki asal sayı olan 2 ve 5’in çarpımı olarak yazılabiliriz. Ve aslına bakarsanız, asal çarpanlarına ayırma, temel eğitim almış herhangi bir kişi için fazla da zor bir süreç değildir. Detaylar için: Asal Sayılar Nedir? Matematikçiler İçin Neden Bu Kadar Önemlidir?
Ancak söz konusu olan yüzlerce basamaklı sayılar olduğunda bildiğimiz yöntemler yararsızdır. Büyük bir sayıyı asal çarpanlarına ayırmak süper bilgisayarlar için bile oldukça zaman alıcıdır. Bu sizi fazla ilgilendirmiyor ise küçük bir not düşelim. Günümüzde internette yaptığımız işlemlerin güvenliği bu sayede sağlanmaktadır.
Asal Sayılar ve Şifreleme
Bilgisayarlarda ve çevrimiçi ortamda veri korumanın merkezinde kriptografi yani şifreleme yer alır. Kriptoloji bir matematik bilimidir ve genelde sayılar teorisi üstüne kuruludur. Bu sayıların başında da asal sayılar gelir. İletişim kurmak isteyen iki kişinin birbirlerine e-posta aracılığı ile ileti göndermesini göz önünde tutalım.
Bu iletiler birçok bilgisayardan geçmektedir. Bir kullanıcıdan diğer kullanıcıya gittiğinde daha önce açılıp okunmadığını veya açılıp üstünde değişiklik yapmadığını bilemeyiz. Bu yüzden devreye şifreleme girmektedir.
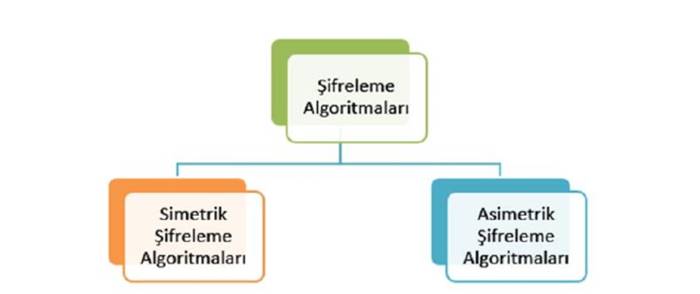
Günümüzde internet üzerinden aktarılan verileri şifrelemek için kullanılan kriptografi yöntemleri iki ana grupta sınıflandırılır: simetrik ve asimetrik yöntemler. Simetrik algoritmaların temel özelliği hem şifreleme hem de şifreyi çözmek için aynı anahtarın kullanılmasıdır. Gönderici, alıcı tarafından da bilinen bir anahtarı kullanarak aktarılacak metni şifrelendirir. Sonrasında da, alıcı da yine aynı anahtarı kullanarak şifreli metni çözer.
Asimetrik sistemlerde bir değil iki anahtar vardır. Bu anahtarların biri açık anahtar, diğeri gizli anahtar biçimindedir. Açık anahtarlar internet üzerinden aktarılır. Ancak şifreli mesajları çözmek, ancak gizli anahtarın bilinmesiyle mümkündür.
Bu durumda biri kilitlemek diğeri de açmak için birbirine uyumlu iki sayıya ihtiyaç vardır. Ayrıca açma anahtarı bilgilerinin de internet sağlayıcı tarafından gizli tutulması gerekmektedir. Buna karşılık kilitleme anahtarı da sizin bilgisayarınızda olmalıdır.
RSA Şifreleme Algoritması

Günümüzde kullanılan asimetrik kriptografi algoritmalarından biri 1977 yılında Ronald Rivest, Adi Shamir ve Leonard Adelman tarafından geliştirildi. İsimlerinin baş harflerinden oluşan bu algoritma RSA algoritması olarak bilinmektedir.
RSA algoritması, en popüler ve güvenli açık anahtar şifreleme yöntemlerinden biridir. Algoritma, çok büyük (100-200 basamaklı) sayıları asal çarpanlarına ayırmanın etkili bir yolu olmadığı gerçeğinden yararlanır.
RSA algoritmasında matematiksel yöntemler ile çalışan iki ayrı anahtar bulunmaktadır. Bu anahtarlardan biri açık diğeri gizli anahtardan oluşmaktadır. Açık anahtarı ile şifreli metin göndermek isteyen bir kullanıcı metni şifreler ve gönderir.
Ancak şifreli metnin çözülebilmesi gizli anahtara sahip olan kullanıcıya bağlıdır. Yani gizli anahtar kimde ise şifreli metni o çözmektedir. RSA algoritmasının güvenirliği kullanılan asal sayıların büyüklüğü ile orantılı olması avantaj iken şifrelemede ve şifre çözme işlemlerinde yavaş kalması en büyük dezavantajlarındandır. RSA algoritmasının arka planındaki matematiği incelemek için bu kaynağa göz atabilirsiniz.
Kuantum Bilgisayarlar ve Kriptografi
Kuantum bilgisayarlar çarpanlara ayırma konusunda kullandığımız sıradan bilgisayarlara göre çok daha hızlı ve başarılı olabilirler. Örneğin, Peter Shor tarafından 1994 yılında kuantum bilgisayarları için geliştirilmiş olan bir algoritma bu işi çok daha kolay hale getiriyor. Bu nedenle matematikçiler bir yandan daha büyük asal sayı ararken, öte yandan güçlü kuantum teknolojilerinin bile kıramayacağı yeni şifreleme algoritmaları geliştiriyorlar.

Gelecekte internet üzerinden aktarılan bilgilerin güvenliğini sağlamanın bir yolu kuantum bilgisayarlar tarafından bile çözülmesi çok zor matematik problemleri olacaktır. Bu amaçla bazı araştırmacılar, asal sayıların yerini matrislerin aldığı algoritmalar üzerine çalışmalar yapıyorlar. Bazı araştırmacılarsa çok değişkenli polinom sistemlerini çözmenin zorluğuna dayalı algoritmalara odaklanıyorlar.
Sonuç olarak zaman içinde asal sayılar tahtını bırakmak zorunda olabilir. Ancak kesin olan bir şey var ki matematiğin gücü her zaman arka planda olacaktır. Ayrıca bu yazımıza da göz atabilirsiniz: Kötü Şifreler, Güçlü Şifreler: Şifre Oluşturma ve Kırmanın Ardındaki Matematik
Kaynaklar ve ileri okumalar:
- The science of encryption: prime numbers and mod n arithmetic; https://math.berkeley.edu
- The Impact of Quantum Computing on Present Cryptography; https://arxiv.org/abs/1804.00200
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel