Fermat’ın İki Kare Toplamı ve 400 Yıl Sonra Gelen Tek Cümlelik Kanıtı

Asal sayılar, geçmişten günümüze dek pek çok insanın ilgisini çekmeyi başarmıştır. Bu yazımızda da yine ilginç bir asal sayı problemini ve çok uzun yıllar sonra gelen tek cümlelik bir kanıtı ele alalım. Bu soruyu ortaya atan kişi de on yedinci yüzyılın Fransız matematikçisi Pierre de Fermat. Bu nedenle de teorem onun adı ile “Fermat’ın İki Kare Toplamı” olarak biliniyor.

Yukarıda bir liste görüyorsunuz. Dönem dönem matematikçiler de listeler yapar. Bu liste de matematikçilerin seçtikleri en güzel matematik teoremlerini bizlere gösteriyor. Yazımızın konusu olan iki kare toplamı da bu listede 10. sırada yer alıyor.

Fermat’ın İki Kare Toplamı Nedir?

Bildiğiniz gibi Pierre de Fermat sayılar ile oynamayı seven amatör bir matematikçiydi. Her ne kadar bir çok kişi kendisinin adını ünlü Fermat’ın son teoremi ile duysa da aslında kendisinin ortaya attığı daha bir çok teorem vardı. Bunlardan bir tanesi yine asal sayılar ile ilgiliydi. Sebebini bilemediğimiz bir nedenden dolayı Fermat bir gün asal sayıların iki kare toplamı biçiminde yazılıp yazılamayacağını merak etmişti. Sonrasında da aşağıda gördüğünüz gibi bir listeye ulaşmıştı.

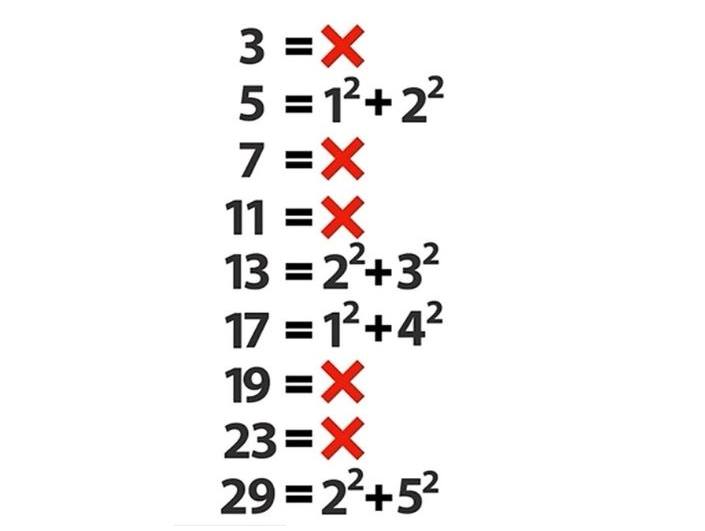
Fermat, yüzlerce asal sayıyı eliyle yaptığı işlemler ile denedi. Sonuçta da iki doğal sayının toplamı biçiminde yazılabilen 100 kadar sayı buldu. Sonra bir anda bu bulduğu sayıların belirli bir model oluşturduğunu da fark etti.

Yukarıya baktığını zaman bu modeli göremiyor olabilirsiniz. Ancak biraz daha ekleme yaparsak yukarıdaki listede, iki kare toplamı biçiminde yazılabilen sayılar 5,13,17, 29, 41… biçiminde devam edecektir. Aralarındaki örüntüyü fark etmeniz kolaydır. Sonuçta bu sayılar 4 sayısının katlarının 1 fazlasıdır. Kısacası hem asal olup hem de iki kare toplamı biçiminde yazılabilecek sayılar k bir doğal sayı olmak üzere 4k+1 biçimindeydi. Aslında yazılamayan sayılar da 4k+3 biçimindeydi.

Aslında Fermat’ın iki kare toplamı ile ilgili problemi budur. Sonucunda kendisi bu ilişkiyi görmüş 1640 yılında görmüş ancak kanıtlayamamıştı. Zaten bildiğiniz gibi kendisi teoremleri kanıtlanmadan bırakma konusunda bir üne sahip idi. Aslına bakarsanız Fermat’tan 15 yıl önce Albert Girard isimli bir başka matematikçi daha aynı ilişkiyi fark etmiş ancak o da bir kanıt sunamamıştı.

Teoreme ilişkin ilk ispat yaklaşık 100 sene sonra Leonard Euler tarafından yapılacaktır. Ancak bu ispat oldukça karmaşık biçimde yapılmıştı.( Merak edenler buradan bakabilirler.)

Devamında da Gauss, Lagrange ve Dedekind gibi önemli matematikçiler tarafından farklı kanıtlar sunuldu. Bunların hepsi önemli katkılar olsa da sadece profesyonel matematikçilerin anlayabilecekleri biçimde ispatlanmıştı. 1990 yılında ise Don Zagier tarafından bu teorem “tek cümle” ile kanıtlandı.

Don Zagier İki Kare Toplamını Nasıl Kanıtladı?

Her ne kadar tek bir cümlelik ispat olsa da yukarıda gördüklerinizin sizin için fazla bir anlam taşımıyor olması da olasıdır. Anlamlandırabilmek için bildiklerimizden yola çıkalım. Fermat’ın iki kare toplamını doğru kabul ederek elimizde p biçiminde bir asalımız olduğunu bu asalın p = 4k+1 biçiminde yazılabildiğini ve aynı zamanda p = a² + b² olacak biçimde de gösterilebildiğini de kabul edelim.

İki kare toplamı ile uğraşırken 2’den büyük asal sayıları dikkate alıyoruz. Bu nedenle p asalının bir biçimde tek sayı olması gerektiğini biliyoruz. Bu durumda a veya b’den bir tanesi çift sayı diğeri ise tek sayı olmak zorundadır. Şimdi bir değişken değiştirme yapalım. Tek olan sayıyı x biçiminde yazalım. Çift olan sayıya ise 2y diyelim. Bu durumda elimizde p= x²+(2y)² biçiminde bir eşitliğimiz var. Buradan da, p = x² + 4yy sonucunu elde ederiz.

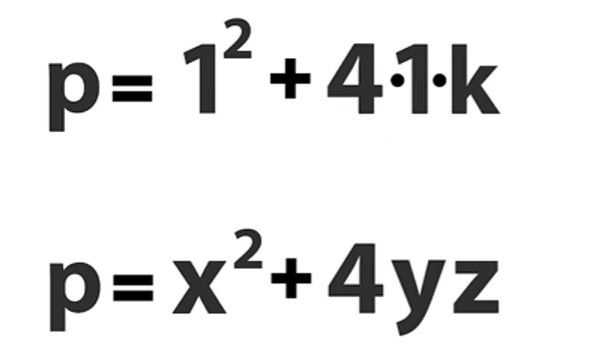
Şimdi elimizdeki y’lerden bir tanesini z ile değiştirelim. Yani eşitliği p = x² + 4yz biçiminde yazalım. Sonrasında da x ve y’i 1 ve k=z kabul edelim. Bu seçimi neden yaptığını anlamak için bir örneği inceleyelim. 37 sayısını ele alırsak ve yukarıdaki formata uygun yazmaya çalışırsak aşağıdaki sonucu elde ederiz.

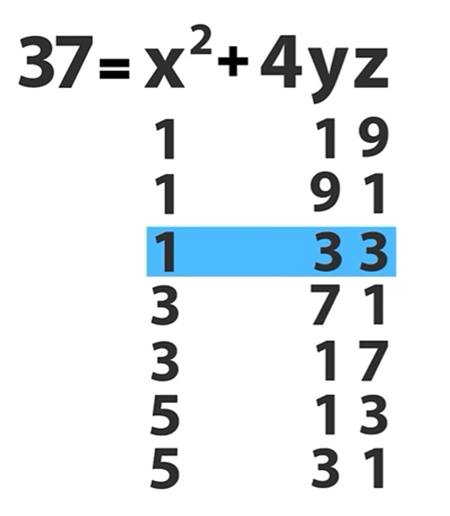
Gördüğünüz gibi 37 sayısını elde etmenin bir çok yolu vardır. Ancak biz sadece y ve z’nin eşit oldukları ile ilgileniyoruz. Ancak bu sayede sayımızı iki kare toplamı biçiminde yazabiliriz. Bu arada y ve z’nin birbirine eşit olmadıklarının çiftler halinde bulunduğuna dikkat edin. Yani y ve z’nin yerleri değişse de sonuç değişmez.

37 sayısını yukarda da görebileceğiniz gibi 7 farklı biçimde yazabiliriz. Benzer biçimde 41 sayısını da 11 farklı biçimde yazabiliriz. Ancak y ve z’nin birbirine eşit olmadıkları durumlar her zaman çift sayıda olacakları için sonucunda genel olarak Fermat’ın iki kare toplamını sağlayan her sayı için her zaman y ve z’nin eşit olduğu bir çözüm bulmak mümkün olacaktır.

İspat Nasıl Tamamlandı?

Aslında fark ettiğiniz gibi şu andan itibaren aradığımız şeyi değiştirdik. Artık Fermat’ın söylemini kanıtlayan genel çözümün tek sayıda farklı biçimde yazılıp yazılamayacağını bulmaya çalışıyoruz. Bunu yapabilmek için de biraz geometriden destek almak zorunda kalacağız.

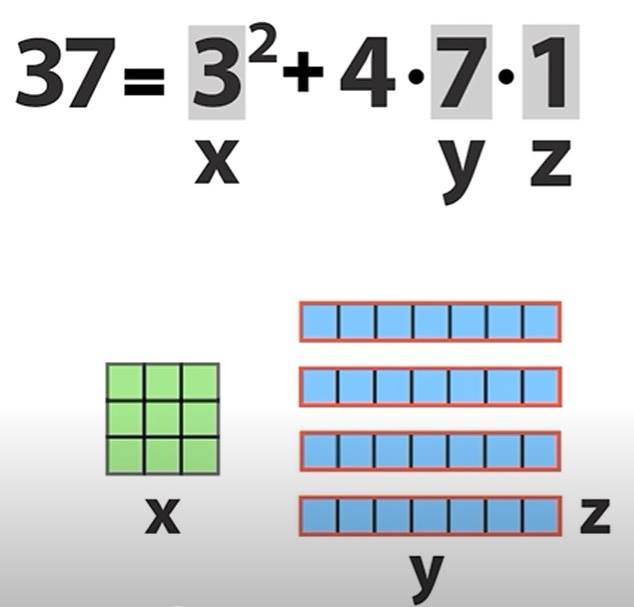
Aşağıdaki 7 şekil 37 sayısının farklı gösterim biçimleri ile oluşturulabiliyor. Alt alta duranlar ise yerlerinin değiştirilmesi sonucunda elde edilen şekilleri gösteriyor. Örneğin orta sırada bulunan şekiller 37=3² +4.7.1 ve 37=3² +4.1.7 sonucunda oluşuyor. Ancak sayfanın en sağında kalan şekle dikkat edelim. Farkındaysanız o tek. Çünkü bu şekil 37=3² +1.3.3 sonucunda oluşmuş durumda.

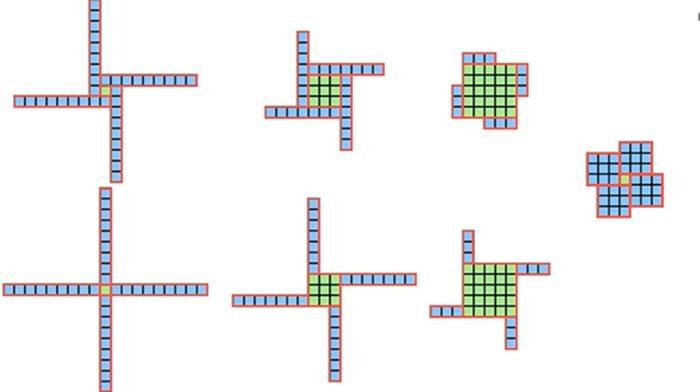
Bu şekillerin her biri merkezdeki kareyi büyüterek ya da küçülterek birbirine eş şekillere dönüşebilir. Ancak sadece bir tanesi dönüşmez. Bu da sol alt köşede gördüğünüz artı şeklidir. Hangi asal sayıyı seçerseniz seçin elinizde her zaman farklı büyüklüklerde olan bir artı olacaktır. Bu da bizi çözüme ulaştıracaktır.

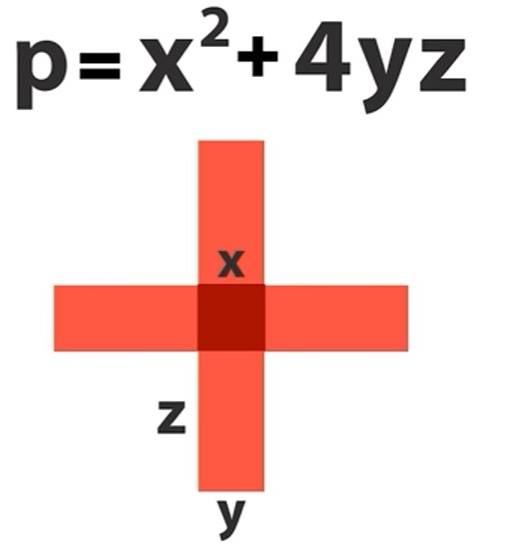
Elimizde kalan artıyı yukardaki görseldeki gibi düşünebiliriz. Buradan x ile y’nin aynı olduğunu anlıyoruz. Bu durumda p = x² + 4xz= x( x+4z) elde ederiz. Şu anda p sayısı iki sayının çarpımı haline geldi. Ancak p sayısının asal olduğunu biliyoruz. Bu durumda x=1 olmalıdır. Bu durumda y’de 1 olacaktır. Ayrıca başta kabul ettiğimiz gibi k=z sonucu ortaya çıkacaktır. Bu sayede p = x² + 4yz ile p = x² + 4yy nin aynı şey olduğunu göstermiş de oluyoruz. Bu aslında Fermat’ın iki kare toplamının kanıtlandığı anlamına geliyor.

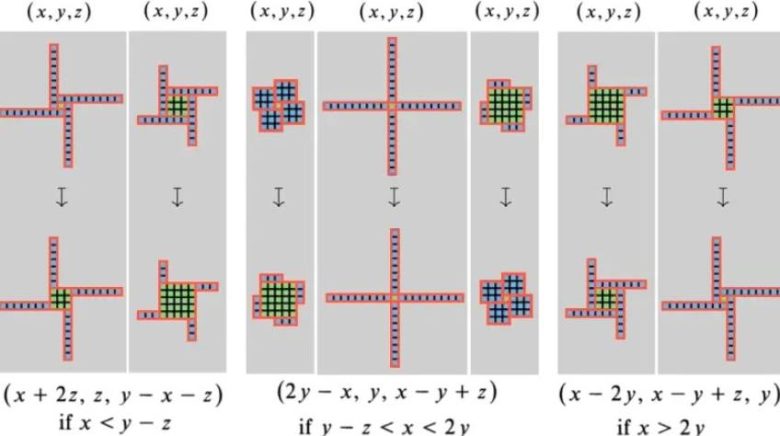
Son olarak Don Zagier’in tek satırlık ispatında yer alan denklemlerin ne anlama geldiğini merak edebilirsiniz. Bu denklemler de aslında bize olası farklı geometrik şekillerin hangi koşullarda birbirine dönüşebildiğini gösteriyor. Kesinlikle çok zekice bir yaklaşımla da sorun çözülmüş oluyor.

Kaynaklar ve ileri okumalar:

• Why was this visual proof missed for 400 years? (Fermat’s two square theorem). Bağlantı: https://www.youtube.com/watch?v=DjI1NICfjOk
• A One-Sentence Proof That Every Prime p 1 (mod 4) Is a Sum of Two Squares; https://fermatslibrary.com/

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel