Birazdan okuyacağınız 4 tane 4 sorusu 1914’te W.W Rouse Ball tarafından yazılan “Mathematical Recreations and Essays” isimli kitapta yayınlandı. Ancak bu sorunun 1890 civarında ilk olarak ortaya çıktığı ve zamanının matematikçileri arasında popüler olduğu da söylenceler arasındadır. Soru oldukça kolay ve şaşırtmaca yok. Size gereken sadece kağıt, kalem ve biraz da boş zaman
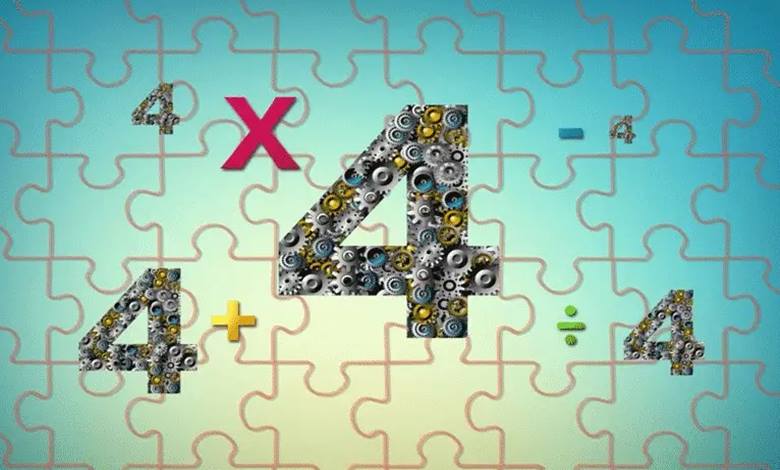
Göreviniz şu: Elinizde sadece 4 tane 4 rakamı olsun. Sadece bu sayıları kullanarak 1’den 100′ kadar tüm sayıları yazabilir misiniz?
Öncelikle Kuralları Belirleyelim
Aslında kurallar oldukça basit. Size kullanmanız için izin verilen işlemler ve semboller şunlar. Dört aritmetik işlemini kullanabilirsiniz. (+, x, -, /). Rakamları birleştirebilirsiniz. Yani 44 sayısı kuralı bozmaz ama bu durumda iki adet 4 kullanmış sayılırsınız.
Ayrıca, ondalık sayılar kullanmak yani 4,4 yazmak da serbesttir. (Ondalık sayıları yazarken bazı zamanlarda 0 rakamını kullanmadan ,4 biçiminde de 4 sayısını kullanabilirsiniz). Son olarak, üstlü sayılar (44 ‘te olduğu gibi ), kare kökler, küp kökler, faktöriyeller (4! gibi) kısacası aklınıza gelen tüm matematiksel işlemleri kullanabilirsiniz. Ayrıca istediğiniz parantezleri de kullanmanıza da izin verilir. Sonuçta, tek şartımız var sadece 4 adet 4 kullanacaksınız.

Şimdiden sizlere hatırlatalım. Bazı sayıları son derece kolay yazabileceksiniz. Ancak üzerinde en çok zaman harcayacağınız sayılar muhtemelen 69 ve 73 sayıları olacaktır. Bu sayıların çözümleri yukarıdaki işlemlerin akıllıca kombinasyonlarını gerektirmektedir.
Aslında, yaklaşık 20’ye kadar olan sayıları sadece temel aritmetik işlemleri kullanarak yazmanız mümkündür. Bu nedenle bu bulmacanın ilk 20 sayıya kadar olan kısmı öğrencileri için keyifli bir alıştırma olacaktır. Ancak tahmin ettiğiniz gibi daha büyük sayılar için toplama, çıkarma, çarpma ve bölme yeterli gelmeyecektir. Neden bahsettiğimizi tam olarak anlamayanlar için öncelikle ilk 20 işlemi yayınlayalım.
4 Tane 4 Rakamı İle Yazabileceğiniz İlk 20 Sayı
Aşağıya sizin için ilk 20 sayıyı ekledik. Gördüğünüz gibi kesinlikle farklı bir biçimde düşünmeniz gerekiyor. Ayrıca elbette 0 = 44 − 44 ; 1 = 44 / 44 ; 3 = (4 + 4 + 4) / 4 veya 5 = (4 × 4 + 4) / 4 düşünmüş olmanız da olasıdır. Çünkü bu sayıları elde etmenin tek yolu yoktur. Önemli olan kurallara uygun hareket etmektir.

Aslına bakarsanız daha büyük sayılar ile uğraşmaya başladığınız zaman sadece toplama, çarpma, çıkarma, bölme dört işlemi ile sonucu bulabileceğiniz sadece 11 pozitif tam sayı daha vardır. Bunlar da aşağıdaki gibidir.
- 24 = (4+4×4)+4
- 28 = ((4+4)x4)-4
- 32 = (4×4)+(4×4)
- 36 = ((4+4)x4)+4
- 48 = (4×4-4)x4
- 60 = 4x4x4-4
- 64 = (4+4)x(4+4)
- 68 = 4x4x4+4
- 80 = (4×4+4)x4
- 128 = (4×4)x4+4)
- 256 = 4x4x4x4
4 Tane 4 Rakamı İle Aslında Her Sayıyı Yazmak Mümkündür
Aslına bakarsanız Nobel ödüllü fizikçi Paul Dirac bu soruyla uğraşana kadar 4 tane 4 rakamı ile kaç sayı yazılabilir sorusu matematikçileri uzun süre meşgul etmişti. Sonucunda matematikçiler bir soruyu kafaya taktıktan sonra kolayca vazgeçmezler. Ancak Paul Dirac olaya farklı bir bakış açısı ile bakarak sonsuza kadar istediğimiz tüm sayıları sadece 4 tane 4 kullanarak yazabileceğimizi göstermişti.
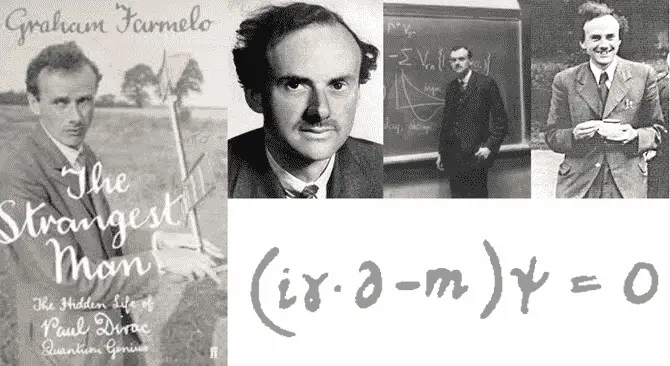
Ancak bunun için işin içine logaritmayı da katmamız gerekiyordu. Unutulanlar için hatırlatalım. Logaritma ( kısaca log) temelde bir üssün tersidir. Bir kaç örnek için aşağıya göz atınız.

4 tane 4 yazmamız için tahmin edeceğiniz Örneğin log4 4 sayısı yazarak bir elde edebilirsiniz. Hatta, 4 tane 4 kullanarak sonsuzluğa bile aşağıda gördüğünüz gibi erişebilirsiniz. Ayrıca log44n=n olacaktır. Burada da n bir tamsayı olmak zorunda değildir. Şimdi √4/4 yazarak iki tane dördümüzü kullanalım. Bu arada √4/4=1/ anlamına gelir. Bu bizim tabanımız olacak. Kalan iki dördümüzü de aşağıda gördüğümüz biçimde kullanırsanız aslında 1 den başlayarak sonsuza kadar olan bütün sayıları sadece 4 tane 4 ile yazmanız mümkün olacaktır.
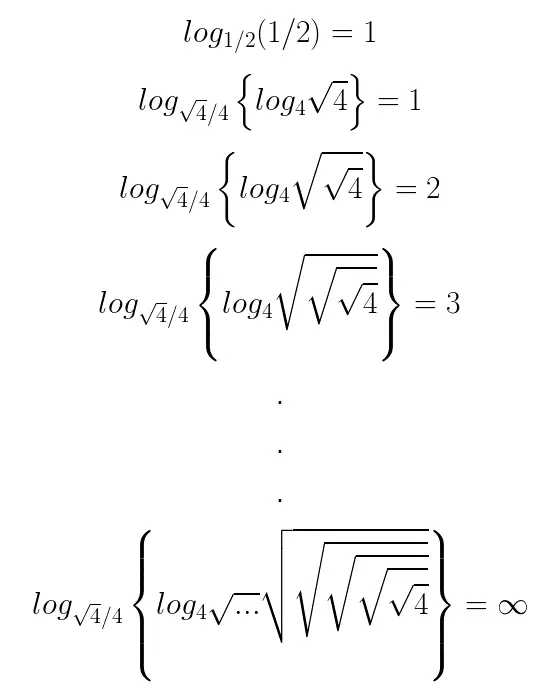
Sonuç Olarak;
Yukarıdaki çözüm moralinizi bozmasın. Herhangi bir doğal sayıyı üretmeye yönelik bu genelleme aslında bulmacayı kesin olarak ortadan kaldırır. Aslına bakarsanız bu nedenle bulmacanın çözümünde logaritmanın kullanılmasına izin verilmez.
Kaynaklar ve ileri okumalar:
- The Four Fours Puzzle; Kaynak site: Wikipedia. Bağlantı: The Four Fours Puzzle;
- What Is The Four Fours Puzzle?. Yayınlanma tarihi: 19 Ekim 2023. Kaynak site: Science ABC. Bağlantı: What Is The Four Fours Puzzle?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





