Sonsuz kelimesi çelişkilerle dolu ve akıl karıştıran bir kavram ancak aklınız karıştığı zaman hemen endişelenmeyin. Bu normal bir durum çünkü sonsuz nedir diye kendinize sormaya başladığınızda tehlikeli bölgelere girmiş olursunuz.

Aslında imkanları olsa matematikçiler sonsuzluğu siler atarlardı belki de. Ancak bu elbette mümkün değil çünkü matematik her açıdan sonsuzluğun izlerini taşır. O zaman sonsuz, sonsuzluk gibi kavramlar hakkında bildiklerimize kısaca göz atalım. Öncelikle klasik bir soru ile başlayalım.
Sonsuz Nedir?
Sonsuzluğu başlangıç düzeyinde tanımlarken akıl edilebilecek en büyük sayı olarak düşünürüz oysa bu yanlıştır. Akıl edilebilen her sayı sonludur. Üstelik sonsuzu sınırsızlık gibi de algılamamak gerekir. Çünkü matematiksel açıdan sonsuz sınırsız olabildiği gibi sınırlı da olabilir. Hatta sayılamaz olduğu kadar sayılabilir de.
Örnek olarak 1,2,3… şeklinde devam eden doğal sayılar kümesini ele alalım. Bu sayılar sınırsızdır ve bütün doğal sayıların birleşim kümesi büyüklük olarak sonsuzdur. Şimdide sayı doğrusunda 0 ile 1 arasında kaç nokta vardır sorusunun cevabını düşünelim.? Cevap elbette yine sonsuzdur, ancak bu sefer sonsuzluğumuz sınırlıdır. Gördüğünüz gibi sonsuz, sınırsız olabildiği gibi sınırlı da olabilir.
Sonsuz Ne Kadar Büyüktür?
Sonsuzluk ile ilgili an garip şey de aslında büyüklükleri ile ilgilidir. Sonsuz işte büyüklüğü mü olurmuş demeyin! Alman matematikçi George Cantor’un 19. yüzyılın sonlarına doğru gösterdiği gibi çeşitli sonsuzluklar vardır. Üstelik bazıları açık bir şekilde diğerlerinden daha büyüktür. Cantor, doğal sayıların sayılamaz çoklukta olmalarına rağmen bir başka sayı ailesi olan reel sayılardan daha az sayıda olduğunu çok zekice bir argüman kullanarak göstermiştir.
Göreceli olarak, A ve B kümelerine bakarak, aynı mı yoksa farklı mı olduklarını karşılaştırabiliriz. Ama her iki kümede sonsuz büyüklükteyse bunu nasıl yapacağız? Elbette öğeleri sayamayız. Başka ne yapabiliriz? Bir an için Cantor gibi düşünelim. A ve B kümelerinin sonlu büyüklükte olduğunu varsayalım. Sonra da kümelerin elemanlarını saymak yerine elemanlar arasında birebir eşleme yapalım.
Büyüklüğünü bilmediğimiz iki kasa hayal edelim, birinde elma diğerinde portakal olsun. Elma-portakal partnerleri oluşturmak için iki kasadan da aynı anda bir elma ve bir portakal çekelim. Eğer kasaların içi aynı anda boşalıyorsa eşit sayıdadırlar. Eğer biri diğerinden daha önce boşalıyorsa kalan kasadaki meyveler daha çoktur.
Konuda ilerlemeden önce bilgilerimizi anımsayalım. Elimizde sonsuz bir kümemiz diyelim ki tam sayılar kümemiz olsun. Bu kümenin bütün elemanlarına bir eklediğimizi düşünelim. Sonrada iki küme arasında 1-1 eşleme yapalım. Aslında ilk kümenin bütün elemanlarına bir değil 100 eklesek de aynı 1-1 eşlemeyi yapabilirdik. Sonsuz bir kümeye sonlu sayıda öğe eklemenin onu büyütmediğini anlamış olduk.
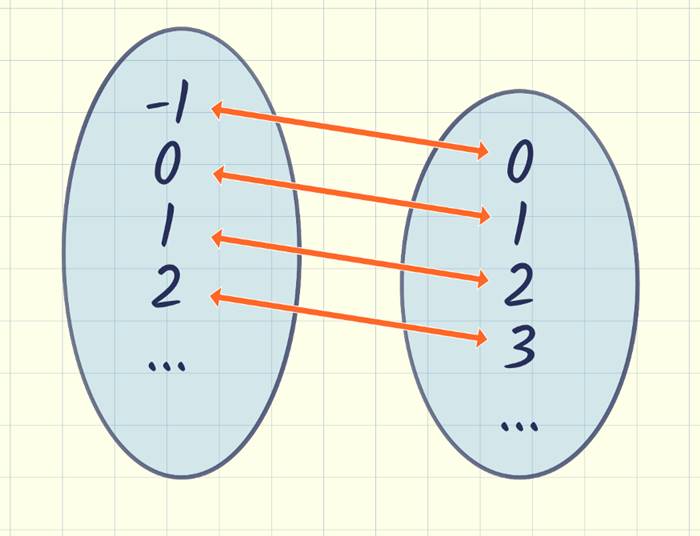
Şimdi doğal sayılar kümesine uygulayalım. Kümemize tüm negatif tam sayıları ekleyelim. Sezgisel olarak bu kümemiz doğal sayılar kümesinden iki kat daha büyük, ancak 1:1 ilişki kurma söz konusu olduğunda bu herhangi bir fark yaratmayacaktır. Görünen o ki, sonsuz bir kümenin boyutunu iki katına çıkarmak onu büyütmedi. Ancak yazının başında hatırlarsanız tek tip bir sonsuz olmadığından bahsetmiştik. Şu ana kadar denediğimiz sonsuzluklar sınırsız olanlardandı. Ve aslında bu sonsuzluklar ile her durumda 1-1 eşleme yapmak mümkün olacaktır. Ancak bir de sınırlı sonsuzlara bakalım.
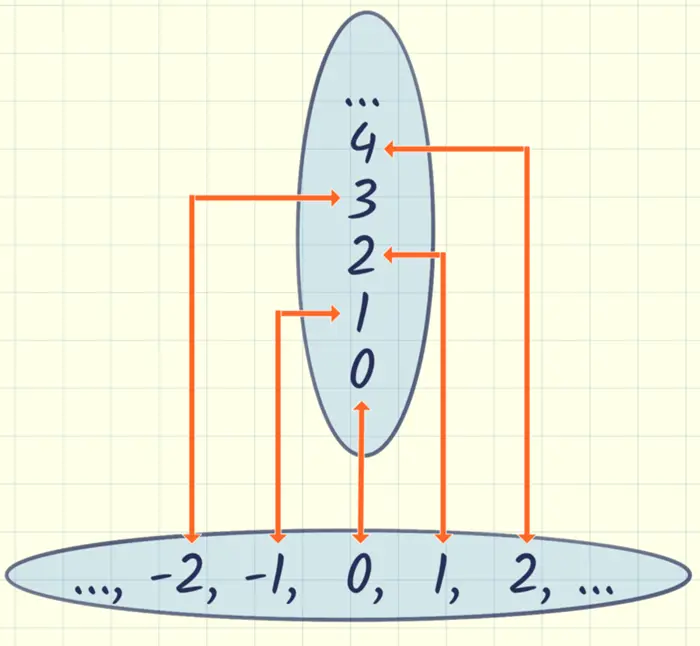
Cantor Soruna Nasıl Yaklaşmıştı?
Cantor bize tam sayılar ve doğal sayılar kümelerinin eşit büyüklükte olduğunu göstermiştir. Hatta Cantor, rasyonel sayıların da doğal sayılarla bire bir eşleşmeye sokulabileceğini kanıtlamıştır. Ancak gerçek sayıların (yani rasyonel ve irrasyonel sayılar) doğal sayılarla bire bir yazışmaya koymanın da mümkün olmayacağını da kanıtlamıştır.

Şimdi elinizde bir reel sayı listesi olduğunu düşünün. Bu liste olası tüm ondalık açılımlı sayıları içersin. Sizin listenize bakarak ben yeni bir reel sayı oluşturacağım. Kural şu: 1.sayınızın virgülden sonraki ilk basamağına bakacağım. Eğer bu sayı 1 ise, ben kendi sayımda 2, değilse 1 alacağım. Ardından listedeki 2. sayınızın 2. basamağına bakacağım ve tekrardan bu sayı 1 ise, benimkini 2 alacağım. Değilse 1 alacağım. Ardından 3. sayınızın 3. basamağına bakacağım ve aynı biçimde devam ederek kendi listemi oluşturacağım.
Sonsuz Nedir Sorusunun Cevabı Kolay Değildir
Sonuçta hiçbir zaman birbirimizin aynısı iki sayı bulma şansımız olmayacaktır. Sonuç olarak reel sayılar sayılamayacak çokluktadır ve reel sayıların sonsuzluğu bir şekilde doğal sayıların sonsuzluğundan daha büyüktür.
Aslında Cantor aynı zamanda bizlere herhangi bir sonsuz kümenin tüm alt kümelerinden oluşan yeni bir küme oluşturulduğunda, orijinal kümeden daha büyük bir sonsuzluk temsil edeceğini gösterdi. Yani, bir sonsuzluğunuz varsa, daima onun alt kümelerinin kümesinden daha büyük bir sonsuzluk elde edebilirsiniz. Zamanında kendisini derin bunalımlara sürükleyen Cantor’un bu tehlikeli düşünceleri bugün tüm matematik araştırmacılara tarafından kabul görmekte.
Kaynaklar ve İleri Okumalar:
- Strange but True: Infinity Comes in Different Sizes; Yayınlanma tarihi: 18 Temmuz 2017. Bağlantı: https://www.scientificamerican.com/
- Infinities are not made equal; Yayınlanma tarihi: 26 Ocak 2020. Bağlantı: https://towardsdatascience.com/
Matematiksel