Borçla ilgili tek iyi şey, matematikteki en önemli sabitlerden biriyle bağlantılı olmasıdır. Bu sayı Euler sayısı ya da Euler sabiti diğer adıyla e sayısıdır. Matematik ve fizikte yaygın olarak logaritmik ve üstel fonksiyonlarda karşımıza çıkar.

Nüfus artışını belirlemede, finansal matematikle uğraştığımız zamanlarda, olasılık ve istatistik hesaplamalarında e sayısı sıkça karşımıza çıkar. Aslında yaşamda değişim ya da büyümeyi içeren bir şey yapmak istediğimizde muhtemelen arka planda bir yerlerde bu sayı gizlidir. Bu yerlerden birisi de bileşik faiz ile bağlantılıdır. Detaylara geçmeden önce, böyle bir sabite neden ihtiyaç duyduğumuza anlayarak işe başlamalıyız.
17. yüzyılda İskoç matematikçi, fizikçi ve astronom Napier, çok büyük sayıları çarpmanın daha basit bir yolunu aramaya başlamıştı. Özellikle, üsler için bir kısayol bulmak istiyordu. Bu çalışmaları esnasında e sayısını keşfetmese de oluşturduğu logaritma listesinin üslerle ilişkilendirilmesine vesile oldu.

1683’te İsviçreli matematikçi Jacob Bernoulli, bileşik faizle ilgili bir finansal problemi çözerken de e sabitini keşfetti. Bunu elbette kredi kartı borçlarımızın çığ gibi neden büyüdüğünü araştırırken değil (1+1/n)n limitinin ne olacağı konusunda çalışırken bulmuştur. Konuyu sonrasında Euler el attı. Sonucunda da bu sabit onun adı ile anılmaya başladı.
e Sayısı ile Bileşik Faiz Nasıl İlişki İçindedir?
Diyelim ki bir yerden %3 yıllık faizle 100 lira borç para aldınız. 3 yıl boyunca da borcunuzu geri ödemediniz. Ödemeye karar verdiğiniz gün ne kadar para planlamanız gerekiyor dersiniz? Eğer matematik ile aranız iyi değilse yıl başına 3 lira fazla ödeyeceğinizi düşünebilirsiniz. Ancak geri ödemeyi planladığınız 109 lira eksik kalacaktır.
Gerçekten de bir yılın sonunda geri ödeme yapmanız gereken miktar 103 liradır. Bunu 100+0,03 x100=103 biçiminde kolayca hesaplayabilirsiniz. Ancak bir sonraki yıl ne kadar borcunuz olduğunu öğrenmek için ikinci yılın faizini eklemeniz gerekir. Önce ödememiz gereken faize bakalım. Bu faiz 0,03x (100 x (1+0,03)) = 3,09 kadar olacaktır. Bunun sonucunda da ikinci yılın sonunda borcunuz. 103+3,09=106,9 lira olmuştur.
Üçüncü yıla geçtiğinizde ise faiz 0,03x (100 x (1+0,03)2)= 3,18 lira olacaktır. Yani üç yılın sonunda ödemeniz gereken toplam borç aslında 106,9+3,18= 109,27 liradır. Bu hesaplamanın neticesinde, her yıl tahakkuk eden faiz tutarının bir önceki yıl tahakkuk eden tutardan fazla olduğunu görebilirsiniz.
Hesaplamanın kolay olması açısından 100 lira borç aldığımızı varsaymıştık. Bu nedenle tahmin ettiğimiz ile hesaplanan sonuç arasındaki fark size fazla rahatsız edici gelmeyebilir. Ancak daha fazlasını aldıysanız, faizin artışı çok belirgindir. Bu da hem borcun laneti ve hem de tasarrufun nimetidir.
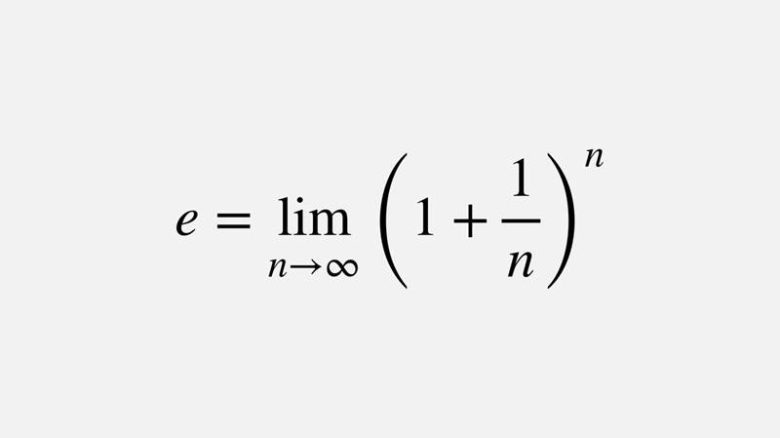
Bileşik Faiz Hesaplaması
Yukarıdaki faiz hesaplamasında bir kalıp görmüş olmalısınız. Aslında bu kalıp da bizi bir formüle götürecektir. Bu formül anapara x (1+ borç yüzdesi) yıl biçimindedir. Matematik dilinde ifade etmemiz gerekirse formül P( 1+ r)n biçiminde yazılabilir. ( Hesaplamalarda faiz yüzdesi yani r ondalık sayı olarak yazılmalıdır. Yani %3=0,03 haline dönüşür.)
Şimdi bu formülün nasıl çalıştığını ve yazının başında söylediğimiz gibi e sayısı ile bağlantısını anlayabilmek için yine işi basitten tutalım. Diyelim ki bu sefer 1 lira paranız var ve bunu bankaya yatırmaya karar veriyorsunuz. Yani P=1. Olmaz ama diyelim ki çok cömert bir banka buldunuz ve yıllık faiz yüzdeniz %100. Bu durum da r=1 olacaktır. Bunları formülde yerine yazıp ilk yılın sonunda toplam ne kadar paranız olduğunu hesaplayalım. Sonuç 1. ( 1+1)2 = 2 liradır.
Şimdi de bankamız size yıllık faiz yerine 3 aylık faiz vermeyi öneriyor. 3 ay bir yılın dörtte biridir. Bu durumda size 4 defa faiz verecek. Şimdi bu bilgileri yerine yazınca bakalım neler olacak. Sonuç 1.(1+1/4)4 = 2,44 lira olacaktır.
Eğer bankanız aylık faiz üzerinden çalışmaya karar verirse bu durumda 1.(1+1/12)12 =2,61 lira elde ederseniz. Ayrıca günlük faiz hesaplaması da yapabilir. Bu da 1.(1+1/365)365 =2,71 lira biçiminde olacaktır. Gördüğünüz gibi elde ettiğimiz formül 1.(1+1/n)n biçimine dönüştü. n sayısı büyüdükçe kazancınız ( çoğu zaman elbette borcunuz) büyümektedir. Saatlik, saniyelik vs gibi bu hesaplamayı çok daha uzatırsanız ulaşacağınız sayı giderek 2,718281828459045… gibi bir sonuca ulaşacaktır.
Euler Sabiti ile Başka Ne Yapabilirsiniz?
Euler sabiti sadece finansta yardımcı olmaz. Diğer bazı yaygın kullanım durumları aşağıda yer almaktadır.
- Olasılık teorisi: Bir rulet oyunu oynuyorsanız ve tek bir sayı üzerine bahis yapıyorsanız, 37 oyun boyunca her oyunu kaybetme olasılığınız yaklaşık 1/e’dir .
- Radyoaktif kimyasalların yarı ömürlerinin hesaplanması.
- Fizikte dalgaların (ışık, ses ve kuantum dalgaları gibi) denklemler hesaplamaları.
Sonucunda başta da dediğimiz gibi yaşamda bir yerlerde bu sayı gizlidir. Yazımızın bitiminde göz atmak isteyebilirsiniz: Paranın Matematiği: 72 Kuralı Nedir Ve Nasıl Çalışır?
Kaynaklar ve İleri Okumalar
- Maths in a minute: Compound interest and e; Yayınlanma Tarihi: 7, Şubat, 2018; Yayınlandığı Yer: Plus.maths; Bağlantı: https://plus.maths.org/
- Wednesday Is E Day. Can We Make It As Fun As Pi Day?; Yayınlanma Tarihi: 7, Şubat, 2018; Yayınlandığı Yer: Slate; Bağlantı: https://slate.com
- Reichert, S. e is everywhere. Nat. Phys. 15, 982 (2019). https://doi.org/10.1038/s41567-019-0655-9
Matematiksel









