Bu yazıda size iki farklı ve kullanışlı antik çarpma yöntemi göstereceğiz. Aslında sizin de kolayca fark edeceğiniz gibi bu iki çarpma işlemi birbiri ile belli bir noktaya kadar bağlantılı. İlk çarpma işlemimiz Rus köylülerden gelsin.

Birazdan göstereceğimiz çarpma işlemi sayesinde, çarpım tablosunu ezberlemeye gerek kalmadan, sadece yarıya bölme ve ikiye katlama işlemi yaparak, istediğiniz büyüklükte iki sayıyı çarpmanı mümkündür. Bu yöntem bir zamanlar Rusya’da köylerde sıkça kullanıldığı için bu ismi almıştır.
Rus Çarpımı (Russian peasant multiplication) Nasıl Yapılır?
Bu yöntemi uygulamak için öncelikler çarpmak istediğiniz iki sayıyı iki sütunun üstüne yazın. Sol sütunda bulunan her sayıyı sürekli ikiye bölmeye başlayın. Bölme sonucunda çıkan buçuklu değerleri dikkate almayın. Sadece tam kısmını yazarak 1 sayısına erişene kadar bölmeye devam edin. Sağ sütunda bulunan, çarpacağınız ikinci sayıyı ise soldaki 1 sayısının karşısına denk gelene kadar ikiye katlayın. Yani kendisi ile toplayın. Bunun bir örneğini aşağıda görebilirsiniz.
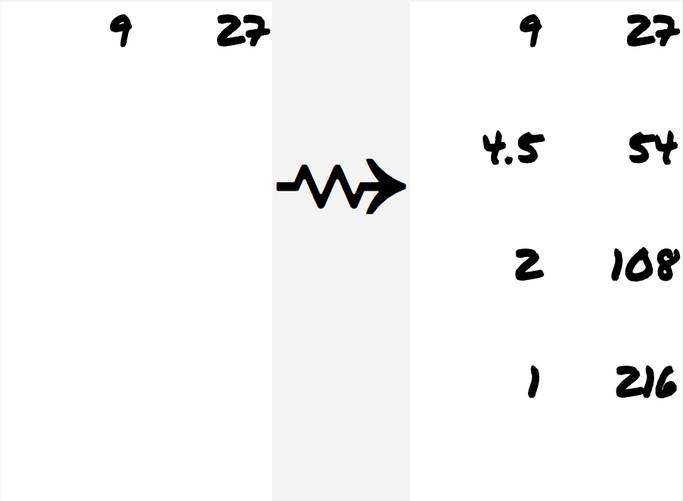
Şimdi yapmanız gereken basit. Sol taraftaki sütunu gözden geçirin ve çift olan satırları silin. Sonrasında ise yanıtı elde edebilmek için sağ sütunda geriye kalan sayıları toplayın.
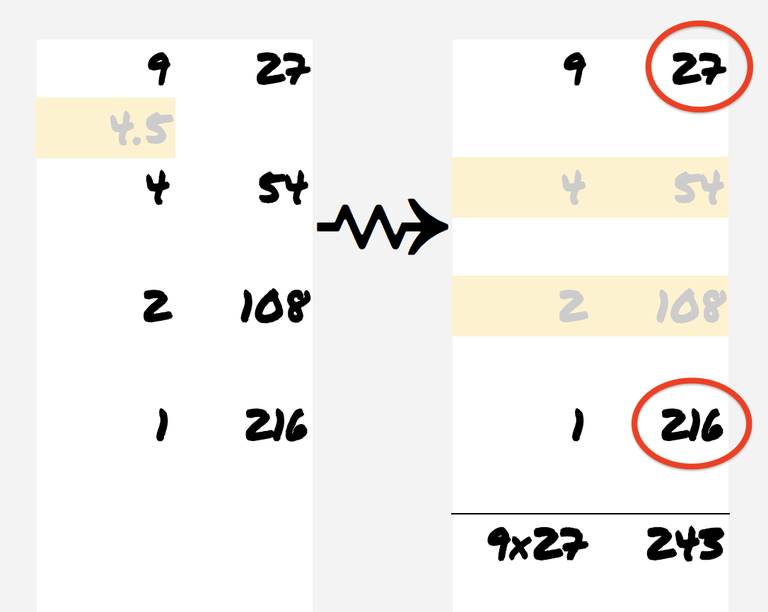
İşlem sırasını değiştirseniz de sonuç değişmeyecektir. Bu çarpma işleminde, hangi sayı ile denerseniz deneyin doğru cevabı bulacaksınız.

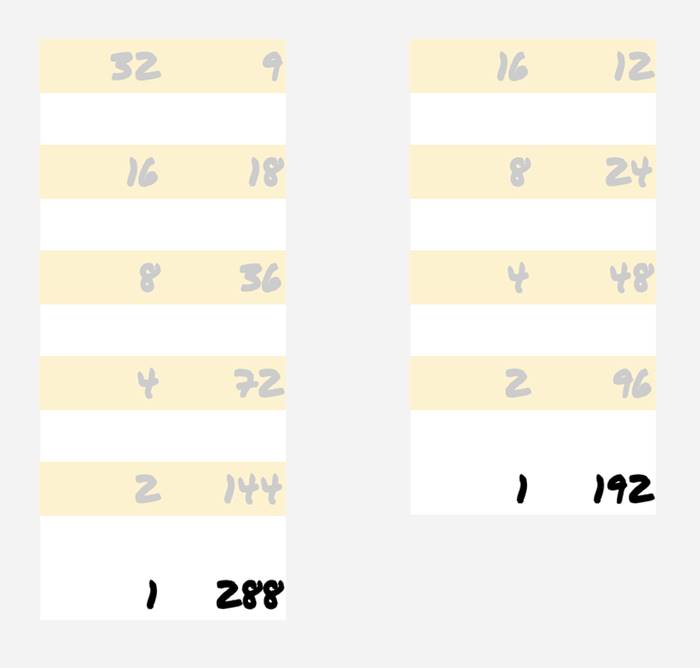
Eğer çarpmak istediğiniz sayı çift ise sonuç daha da eğlenceli bir hal alıyor. Toplama işlemi yapmadan direk cevabı elde ediyorsunuz.
Rus Çarpımı Neden İşe Yarıyor?
Bu yöntemin işe yaramasının nedeni ikilik sayı sistemi üzerinde çalışmasıdır. Günümüz teknolojisinin temelinde yer alan ikilik sistem temelde sadece 1 ve 0 sayılarını içermektedir. Günlük yaşantımızda kullandığımız 10’luk sistemde sayıların basamakları birler, onlar gibi 10 sayısının katları olacak biçimde düzenlenmiştir. İkilik sistemde ise basamaklar iki sayısının katları biçimindedir. Bununla ilgili aşağıdaki örneklere göz atabilirsiniz.
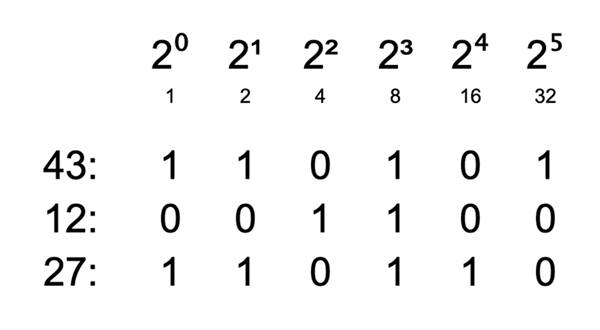
Aslında verdiğimiz yukarıdaki örneklere bakarak Rus usulü çarpma işleminin neden işe yaradığını anlamaya başlamış olabilirsiniz. Örneğin 27 sayısını ele alın. Karşısında 1 yazan değerleri toplayın. Yani 20 + 21 +23 +24. Bu toplamınız 27 yapacaktır. Bunda elbette şaşılacak bir şey yok. Ancak az evvelki Rus Çarpımını hatırlayın. Orada yaptığımız şey soldaki çift değerleri silmek ve geriye kalanları toplamaktı. Çift değerlerin ikilik sayı sisteminde 0’a denk geldiğini hatırlayalım.
Bu yöntem ile Mısır çarpması birbirine bir çok açıdan benzemektedir. Sadece aralarında küçük bir fark vardır. Rus çarpımının ilk ne zaman kullanılmaya başladığı belirsiz olduğu için ilk kimin fikri olduğunu kesin bilemeyiz. Ancak kişisel fikrim ilk Mısır çarpmasının olduğudur.

Mısır Çarpması Nasıl Yapılır?
Bildiğiniz gibi matematik başlangıçta pratik problemlere çözüm aracı olarak kullanılmaya başlanmıştır. M.Ö. 1600 yıllarından kalma Rhind papirüsü, antik Mısır’dan günümüze ulaşmış en kapsamlı matematiksel dokümandır. İçinde arazi alan ölçümü, mali hesaplamalar ve belli sayıdaki ekmeği belli sayıdaki insan arasında bölüştürme gibi konular içeren 84 problem bulunmaktadır.
Mısırlılar bu problemlerini cümleler ile ifade etmişlerdi. Sonuçta ellerinde bugün sahip olduğumuz ayraçlar, eşit işaretleri ya da x’ler gibi sembolik araçlar olmadığı için problemleri deneme yanılma yöntemi ile çözüyorlardı. Onların matematiksel bilgileri hakkında bildiklerimizin çoğunu bu papirüsten öğrendik. Bu çarpma işlemi de aynı kaynakta yer almaktadır.
Bir kere daha sayıları iki sütun halinde düşünceyiz. Ancak bu sefer ilk sütun 1 ile, ikinci sütun ise ikinci çarpanla başlayacak. Sonra yapmamız gereken şey aslında çok basit. Her iki sütundaki sayının da sırasıyla iki katını almalıyız. Aşağıdaki çarpma işlemini inceleyelim. Tabloda da gördüğünüz gibi ikiye katlama işlemini sol sütunda sayıya en yakın ama sayıdan küçük olan katı bulduğumuz zaman durdurmamız gerekiyor.

Neden ikinin bazı kuvvetleri kırmızı bazıları yeşil renkte diye merak edebilirsiniz. Fark ettiyseniz ikinin sadece çift kuvvetleri kırmızı. Bu kuvvetlerin toplamı da yani 85 = 1 + 4 + 16 + 64 bizim ilk çarpanımızı oluşturuyor. Diğer bir deyişle, 85 sayısının (1010101)2 biçiminde iki tabanında gösterimine karşılık geliyor. Sonuç olarak yapmamız gereken tek şey karşılarındaki sayıları toplamak.

Sonuç olarak;
Eski insanlar da yaşadıkları dönemde bizim gibi matematik yapmak zorundaydılar. Ancak bunun için bizim sahip olduğumuz araçlara sahip değildiler. Günümüzde okullarda öğrendiğimiz çarpma yöntemi parçalara ayırma, sonradan birleştirme gibi bir çok adım içerir. Oysa ki yarıya bölme ve ikiye katlama çarpım tablosu bilmeyen biri için ideal bir yöntemdir. Okullarda bir şekilde bu yöntemin de mutlaka gösterilmesi gerektiğini düşünüyoruz.
Kaynaklar ve ileri okumalar:
- The Russian Way to Multiply Is So Much Cooler Than Ours; yayınlanma tarihi: 6 kasım 2020; Bağlantı: https://www.popularmechanics.com/
- Russian Multiplication – Numberphile; Yayınlanma tarihi: 4 Şubat 2020; Bağlantı: https://www.youtube.com/
- Egyptian Multiplication; Bağlantı: https://www.cut-the-knot.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel