Hareket halindeki bir aracın penceresinin dışına baktığınızda, size yakın konumda olan nesnelerin hızlı bir şekilde ancak uzaktaki nesnelerin daha yavaş hareket ettiğini fark ettiniz mi? Buna paralaks etkisi denir. Paralaks, bakış açısı değiştiğinde, daha uzak bir arka plan nesnesine göre ön plan nesnesinin konumundaki belirgin değişikliktir. Bu tanım kafa karıştırıcı geliyorsa, şu basit deneyi yapın.
İşaret parmağınızı burnunuzdan yaklaşık 6 cm uzakta tutun. Şimdi sol gözünüzü kapatın ve parmağınızın arka plandaki nesnelere göre nasıl hizalandığına dikkat edin. Sonra sol gözünüzü açın ve sağı kapatın. Ne oldu? Muhtemel arka planın göreceli konumu sola kaymıştır.

Gözlemlediğiniz bu açısal değişiklik, paralaks sonucunda olur. Paralaks, parmağınızla burnunuz arasındaki mesafe ve gözlerinizin arasındaki mesafeyle doğru orantılıdır. Örneğin, parmağınızı burnunuzdan bir kol uzunluğuna kadar ileriye doğru uzatırsanız paralaks kayması miktarı azalacaktır.
Paralaks İle Gökcisimlerinin Uzaklığı Arasındaki İlişki Nedir?
Günümüzün güçlü teleskoplarının kullanılmasından çok uzun zaman önce gökyüzü gözlemcileri hesaplamalarını matematiksel yöntemleri temel alarak yaparlardı. Ancak astronomlar için en önemli sorun uzaklıkları ölçmekti. Buna bir çözüm olarak da uzunca bir süre bilim insanları geometriden faydalanan bir hesaplama yöntemini yani paralaks yöntemini kullanacaktı.

ve özdevinimlerini bulmaya adamıştır. . 1830’larda teleskopların gücündeki iyileşmelerle birlikte, yıldız paralaksının ilk doğru ölçümünü yapma yarışı başlayacak ve ipi ilk göğüsleyen de o olacaktı.
Paralaksı kullanarak yakındaki yıldızların uzaklığını ölçmenin olanaklı olabileceği düşüncesi çok uzun süre boyunca bilinse de bu yöntemi kullanarak bir yıldızın uzaklığını doğru ölçen ilk astronom ise1838’de Friedrich Bessel olacaktı.
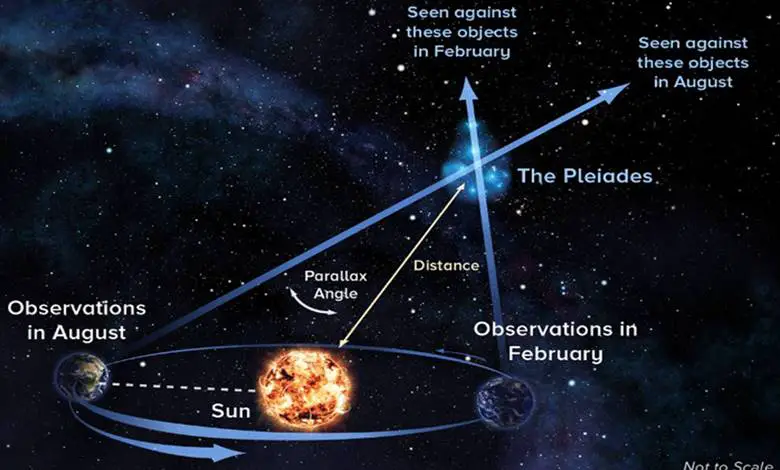
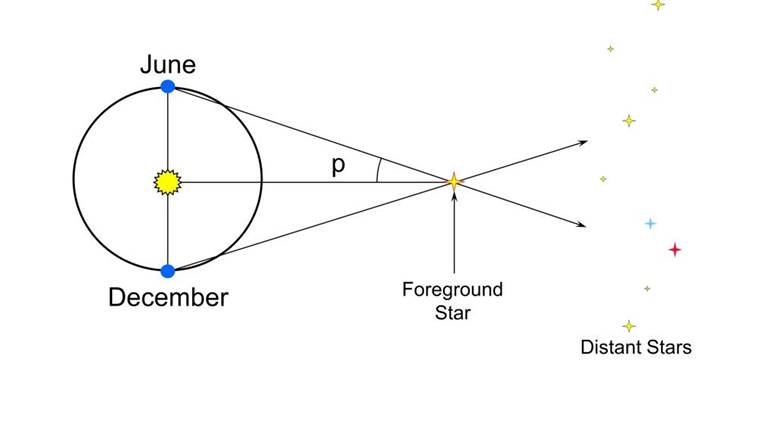
Bu fenomene göre yakındaki yıldızlar, Dünya kendi yörüngesinde dönerken daha uzak yıldızlara göre konumlarını değiştiriyormuş gibi görünmelidirler. Bunu daha iyi anlamak için aşağıdaki görsele göz atınız. Paralaks etkisi nedeniyle yakındaki bir yıldızın arkasında yer alan yıldızlara göre görünür konumu, Hazirandaki 1 noktasından Aralıktaki 2 noktasına hareket eder. Bu sayede gökbilimciler yakındaki yıldızlara olan mesafeyi oldukça doğru bir şekilde hesaplar.
Paralaks Nasıl Hesaplanır?
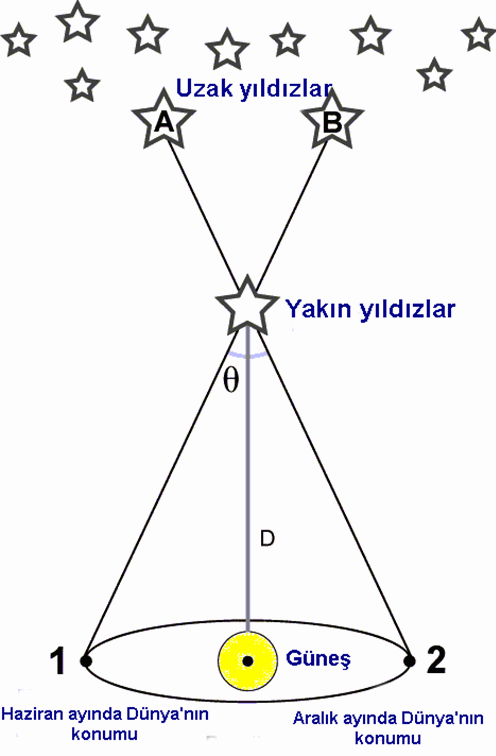
Ancak bu hesaplamayı yapabilmek için bir gökbiliminin bazı kesin ölçümlere ihtiyacı olacaktır. Bunun için ilk olarak, bir gökbilimci bir yıldızın gece gökyüzündeki konumunu not eder. 6 ay sonra aynı yıldızın konumunu tekrar ölçer. Bu iki konumun karşılaştırılması sonucunda da paralaks açısı bulunabilir.
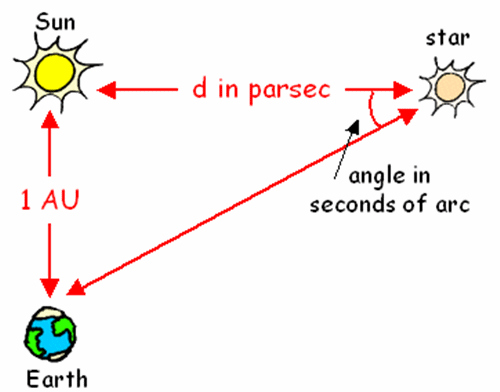
Paralaks formülü, p = 1 / d biçimindedir. P, yıldızın gökyüzünde görülen açısal kaymasını ( ark saniye cinsinden) ve d ise yıldıza olan uzaklığı (parsek cinsinden) ifade eder. Bir parsek paralaksı 1 olan bir gökcisminin uzaklığına denktir ve yaklaşık 3,26 ışık yılına eşdeğerdir.
Aslında bu hesaplama basit bir trigonometri hesabıdır. Bunun için şekli yanlamasına düşünelim. Yıldıza olan mesafeyi hesaplamak için Güneş’in konumundan yıldıza dik bir çizgi çizelim. Dünya’dan Güneş’e olan mesafeyi sonucunda biliyoruz. Bu sayede dik üçgenler yardımı ile paralaks açısını buluruz.
Uzaktaki Gökcisimlerinin Uzaklığının Hesaplanması
Güneş sistemimize en yakın yıldız, dört ışık yılı uzaklıktaki Alpha Centauri’dir. Ancak, en yakın yıldız bile Güneş’imizden 1 parsek uzaktadır. Dolayısıyla, bir yıldıza olan uzaklığı saptamak için gökbilimcilerin yıldızlardaki bu yer değiştirmeleri 1 ark saniyeden daha küçük bir birim kullanarak ölçmesi gerekir.
Ancak yıldız ne kadar uzakta olursa, altı aylık konumundaki değişimi ölçmek o kadar zorlaşır. Paralaks yöntemi bu nedenle yalnızca 100 parsekten daha yakın yıldızlar için işe yarar. Ancak çoğu yıldız bu aralığın dışında kalır.
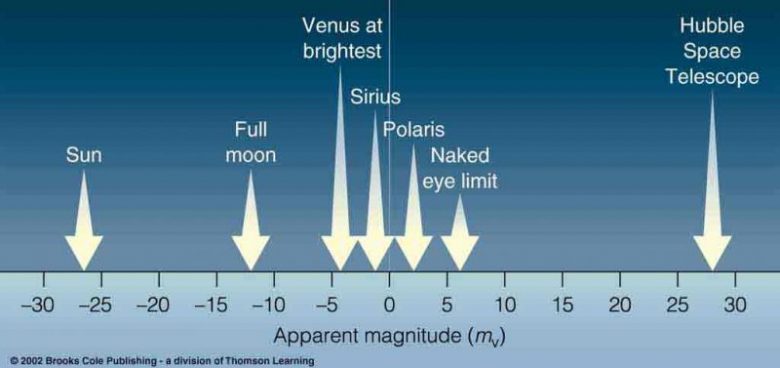
Bir yıldızın en önemli özelliklerinden biri parlaklığıdır. Gökyüzüne baktığınızda da bazı yıldızlar diğerlerinden çok daha parlak görünür. MÖ 150’de Yunan gökbilimci Hipparchus bunu fark etmiş ve yıldızları parlaklıklarına göre sınıflandırmaya çalışmıştı.
Hipparchus her yıldızı altı büyüklük sınıfından birine atamıştı. En parlak 20 yıldıza 1, sonraki en parlak gruptaki yıldızlara 2 olacak biçimde bir derecelendirme sistemi geliştirmişti. Bugün hala, Hipparchus’un geliştirdiği sistemin genişletilmiş halini kullanıyoruz.
Renk / Büyüklük İlişkisi
Bununla birlikte, bu ölçek de yanıltıcı olabilir. Çok parlak, ancak gerçekten uzak bir yıldız varsa, o zaman sönük gözükecektir. Dünya’ya daha yakın olan ise daha parlak olacaktır. Bu nedenle yıldızların farklı parlaklıkları, görünür büyüklüklerle değil, mutlak büyüklüklerle ölçülür.
İki büyüklüğü karşılaştırarak, yıldızın bizden ne kadar uzakta olabileceğine dair bir tahmin yapabiliriz. Bunu şöyle düşünün. Size doğru giden bir araba hayal edin. Farın gerçek parlaklığını biliyorsanız, size doğru gelen ışığın ne kadar parlak göründüğüne bağlı olarak arabanın sizden uzaklığını kolayca anlayabilirsiniz.
Ancak son bir sorunumuz daha vardır. Bir yıldızın mutlak büyüklüğünün ne olduğunu belirlemenin mükemmel bir yolu yoktur. İşte bu noktada da yıldızların renklerini analiz ederiz. Yıldızlar beyaz, mavi, kırmızı ve hatta sarı renkli olabilmektedir.

Gökbilimciler yıldızların rengini, renk filtreleri sayesinde belirleyebilirler. Beyaz veya mavi yıldızlar genellikle sarı yıldızlardan, sarı yıldızlar da kırmızı yıldızlardan daha parlaktır. Temel olarak, bir yıldızın rengi yüzey sıcaklığını belirler.
Yukarıda açıklanan tüm bunların yanı sıra, gökbilimcilerin yıldız mesafelerini için başka ölçüm araçlarına da sahiptir. Periyot- parlaklık ilişkisi, Sefe değişen yıldızlarını kullanmak da bunlardan birisidir. Bu yöntem diğer yöntemlerle hesaplanamayacak kadar uzak olan nesnelerin mesafelerinin tespiti için inanılmaz derecede yararlıydılar. Bu yöntemin detaylarını öğrenmek için bu yazımıza göz atabilirsiniz: Bize Evrensel Bir Cetvel Veren Henrietta Leavitt İle Tanışın
Kaynaklar ve İleri Okumalar:
- Adam Frank; Astronomy At Play İn Cosmos; W. Norton, Inc.; ISBN 978-0-393-93522-6
- How can I measure the distance of a star? (Beginner); http://curious.astro.cornell.edu/physics
- How are astronomers able to measure how far away a star is?; https://science.howstuffworks.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





