Monty Hall Problemi, adını Amerikan yarışma programı Let’s Make a Deal’ın sunucusu Monty Hall’dan alır. Problem, Parade dergisinde yayımlanan bir köşe yazısında verilen yanıtın ardından geniş çapta tartışma konusu hâline gelmiştir.

Bu problemde yarışmacılara üç kapıdan birini seçme hakkı tanınır. Kapıların birinin arkasında otomobil gibi son derece cazip bir ödül bulunurken, diğer iki kapının arkasında keçi gibi daha az değerli ödüller yer alır.
Monty Hall problemi, filmlerden televizyon dizilerine, hatta şarkılara kadar uzanarak popüler kültüre de sızmıştır. Bu problem, sezgi ile olasılık arasındaki ilişkinin her zaman basit olmadığını hatırlatır. İçerdiği mantıksal ve istatistiksel akıl yürütme ile ilk bakışta paradoksal görünen sonucu, Monty Hall problemini dünya genelinde olasılık ve istatistik derslerinin en sevilen konularından biri hâline getirmiştir.

Monty Hall Problemi Nedir?
Kendinizi bu yarışma programında hayal edin. Sizden üç kapıdan birini seçmeniz istenir (bunları Kapı 1, Kapı 2 ve Kapı 3 olarak adlandıralım). Seçiminizi yaptıktan sonra (örneğin Kapı 1’i seçtiğinizi varsayalım), kapıların arkasında ne olduğunu bilen sunucu, sizin seçmediğiniz kapılardan birini (örneğin Kapı 3’ü) açar ve arkasında bir keçi olduğunu gösterir.
Ardından size yeni bir seçenek sunulur. İlk kararınıza sadık kalabilir (bu durumda Kapı 1’de kalırsınız) ya da kapalı kalan diğer kapıya (Kapı 2) geçebilirsiniz. Burada önemli bir nokta vardır. Sunucu her zaman sizin seçmediğiniz ve arkasında keçi bulunan bir kapıyı açar. Bu, oyundaki gerilimi artırmak için yapılan bilinçli bir tercihtir.
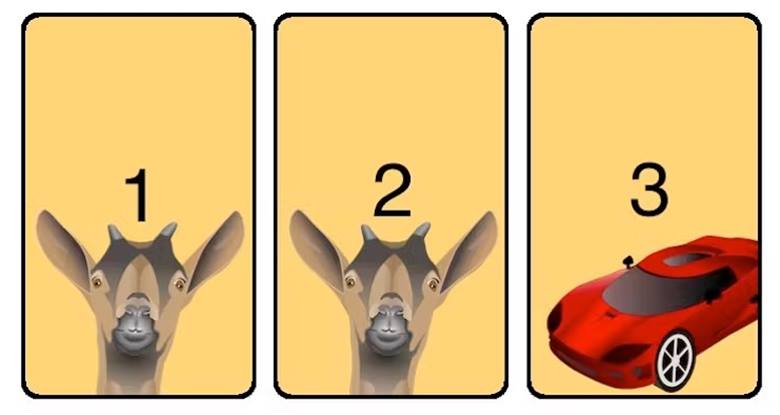
Monty Hall probleminin sorduğu temel soru şudur. İlk seçiminizde mi kalmalısınız, yoksa kapalı kalan diğer kapıya mı geçmelisiniz?
İlk bakışta, otomobili kazanma olasılığının ilk seçiminizde kalmanızla kapı değiştirmeniz arasında aynı olduğu düşünülebilir. Sonuçta açılmamış yalnızca iki kapı kalmıştır. Bu da her bir kapının arkasında otomobil olma ihtimalinin %50 olduğu izlenimini verir. Ancak bu sezgisel değerlendirme yanlıştır.
Parade dergisindeki köşesinde Marilyn vos Savant, olasılığın her iki seçenek için de %50 olmadığını; kapı değiştiren yarışmacının otomobili kazanma şansının daha yüksek olduğunu savunmuştur. Çok sayıda itiraz almasına rağmen, bu yanıt dikkatli biçimde incelendiğinde geçerliliğini korumaktadır.

Monty Hall Probleminin Çözümü Nedir?
Yarışmacı ilk kapıyı seçtiğinde, otomobilin bu kapının arkasında olma olasılığı 3’te 1’dir. Buna karşılık, otomobilin seçilmeyen diğer iki kapıdan birinin arkasında olma olasılığı 3’te 2’dir. Sunucu, arkasında keçi bulunan bir kapıyı açarak ek bilgi sunsa da bu temel olasılıklar değişmez. Yalnızca otomobilin nerede olmadığı göstermiş olur.
Dolayısıyla yarışmacı ilk seçiminde kalırsa, otomobili kazanma olasılığı 3’te 1 olarak kalır. Buna karşılık kapı değiştirildiğinde, otomobili kazanma olasılığı 3’te 2’ye yükselir. Kapı değiştirmek, diğer iki kapıyı birlikte seçmek anlamına gelir ve bu da kazanma ihtimalini iki katına çıkarır.
Bu sonucun nasıl ortaya çıktığını daha iyi anlamak için durumu adım adım inceleyelim:
- Otomobil Kapı 1’in arkasındaysa ve siz Kapı 1’i seçip kararınızı değiştirmezseniz, otomobili kazanırsınız. Bu durumun gerçekleşme olasılığı 3’te 1’dir.
- Otomobil Kapı 2’nin arkasındaysa ve siz başlangıçta Kapı 1’i seçtiyseniz, sunucu arkasında keçi bulunan Kapı 3’ü açar. Bu durumda Kapı 2’ye geçerseniz otomobili kazanırsınız. Bu olasılık 3’te 2’dir.
- Otomobil Kapı 3’ün arkasındaysa ve siz başlangıçta Kapı 1’i seçtiyseniz, sunucu bu kez arkasında keçi bulunan Kapı 2’yi açar. Eğer Kapı 3’e geçerseniz otomobili kazanırsınız. Bu durumun gerçekleşme olasılığı da 3’te 2’dir.
Bu değerlendirmeden görülebileceği üzere, Monty’nin açmadığı kapıya geçildiğinde otomobili kazanma olasılığı 3’te 2, ilk seçime sadık kalındığında ise 3’te 1’dir.
Bu olasılıkların ortaya çıkmasında sunucunun bilgisi ve davranışları belirleyici bir rol oynar. Eğer sunucu kapıların arkasında ne olduğunu bilmiyor olsaydı ya da rastgele bir kapıyı açsaydı, kazanma olasılıkları gerçekten de %50–%50 olurdu.
Çünkü bu durumda sunucu yanlışlıkla otomobilin bulunduğu kapıyı da açabilirdi. Ancak Monty her zaman sizin seçmediğiniz ve arkasında keçi bulunan bir kapıyı açtığı için, olasılıklar kapı değiştirme lehine kayar.
Monty Hall Problemini Daha iyi Anlamak İçin
Monty Hall problemi, sezgilerimizle çelişiyor gibi göründüğü için kavranması zordur. İnsan beyni karmaşık durumları basitleştirme eğilimindedir ve açılmamış iki kapı kaldığında, her iki seçeneğin de kazanma olasılığının %50 olduğu varsayımına kolayca düşer. Ancak Monty Hall problemi, olasılıkların doğru biçimde anlaşılmasının dikkatli bir değerlendirme ve mantıksal bir çözümleme gerektirdiğini açık biçimde ortaya koyar.
Monty Hall problemini kavramakta hâlâ zorlanıyorsanız, onu uygulamalı olarak görmek faydalı olabilir. Çevrim içi pek çok simülasyon, Monty Hall oyununu defalarca oynamanıza imkân tanır. Zamanla, kapı değiştirmenin gerçekten de yaklaşık 3’te 2 oranında kazandırdığını gözlemleyebilirsiniz.

Monty Hall probleminin tarihçesi, sanılanın aksine 1960’lı yıllardan çok daha öncesine uzanmaktadır. Bu problemin temelinde, Üç Kutu Paradoksu olarak bilinen klasik bir olasılık sorusu yer alır. Söz konusu paradoks, Fransız matematikçi Joseph Louis François Bertrand (1822–1900) tarafından ortaya atılmıştır.
Paradoks, Monty Hall problemine oldukça benzer bir kurguya sahiptir. Başlangıçta içerikleri bilinmeyen üç kutu ile başlar. Her kutunun iki çekmecesi vardır. Kutulardan birinin iki çekmecesinde de birer altın bulunmaktadır. İkinci kutunun her iki çekmecesinde ise birer gümüş para yer alır. Üçüncü kutuda ise bir çekmecede altın, diğer çekmecede gümüş para bulunmaktadır.
Rastgele bir kutu seçildikten sonra, bu kutudan rastgele bir çekmece açıldığını ve içinden altın çıktığını varsayalım. Bu durumda, aynı kutudaki diğer çekmecede de altın bulunma olasılığı nedir? Görüldüğü gibi bu soru, yapısal olarak Monty Hall problemine oldukça yakındır ve benzer sezgisel hatalara yol açar.
Sonuç olarak
Monty Hall problemi, olasılığın zaman zaman sezgiye aykırı olabileceğini çarpıcı biçimde gösteren bir örnektir. Defalarca tartışılmış, analiz edilmiş ve doğrulanmış olmasına rağmen hâlâ merak uyandırmaya ve kafa karıştırmaya devam etmektedir. Bu problem açık bir ders sunar: Olasılık söz konusu olduğunda sezgiler her zaman güvenilir değildir.
Kaynaklar ve ileri okumalar:
- A Point of View: Why embracing change is the key to happiness. Yayınlanma tarihi: 8 Ekim 2013. Bağlantı: A Point of View: Why embracing change is the key to happiness2
- Myths of maths: The Monty Hall problem; yayınlanma tarihi: 23 mart 2020. Bağlantı: Myths of maths: The Monty Hall problem/
- Here’s the easiest way to understand the Monty Hall problem. The mathematics puzzle about goats that even PhD-holders get wrong; Yayınlanma tarihi: 3 Aralık 2016. Bağlantı: Here’s the easiest way to understand the Monty Hall problem. The mathematics puzzle about goat/
Matematiksel