
Cebir, sayıları temsil etmek için x ve y gibi sembollerin kullanıldığı denklemlerin dilidir. Ancak “Hangi sayının karesi -1 yapar?” ya da cebirsel olarak ifade edersek x2=-1 sorusunu sorarsak bunun reel sayılarda bir karşılığı yoktur. Çünkü bu sorunun cevabının -1’in karekökü diğer deyişle x=√ -1 biçiminde olur. Bu da bizi sanal sayılar fikrine götürecektir.
Sanal (imaginary) sayılar adı, filozof ve matematikçi Rene Descartes tarafından 1637 yılında verildi. Devamında da Euler bu sayılara bir kimlik kazandırdı. Bu sayede de √-1 , “i” olarak gösterilmeye başlandı.

Sanal sayılar işin içine karıştığı zaman karşımıza yeni bir sayı sistemi çıkar. Bu sistemin adı karmaşık sayı sistemidir. Artık yeni sistemimizde 1, 2 gibi sayıların yanı sıra 1+2i, -3+i gibi sayılar da vardır. Ancak karmaşık sayılar sadece matematiksel araçlar olarak kalsaydı, muhtemel çok fazla kişinin ilgisini çekmezdi. Neyse ki öyle olmadı. ( Bu arada biraz detay öğrenmek isterseniz: Karmaşık Sayılar Nedir ve Neden Öğrenmemiz Gerekir?)
Sanal Sayılar Sadece Matematikçilerin Değil Fizikçilerin de İlgisini Çeker
Karmaşık sayılar ve sanal sayıları öğrenen öğrencilerin aklına çoğu zaman bu benim ne işime yarayacak sorusu gelir. Aslında bir yerde de haklıdırlar. Sonucunda gündelik hayatımızda sanal sayılar ile fazla karşılaşmayız. Aslına bakarsanız karşılaşsak bile bunun farkında olmayız.
Oysa ki Michael Faraday 1830’larda alternatif akımı keşfedince de karmaşık sayılar fiziksel bir gerçekliğe bürünecekti. Sonrasında da bilimsel ilerlemeler neticesinde, matematiğin ve fiziğin başka alanlarında da karşımıza çıkmaya başladı. Günümüzde parçacık fiziği, elektrik mühendisliği gibi birçok bilimsel alan karmaşık sayılara güvenir hale geldi.
Sanal sayılar, uzun zamandır kuantum mekaniğinin en önemli denklemlerinde karşımıza çıkıyor. Sonuçta kuantum mekaniğinin temel denklemi olan Schrödinger dalga denklemi de aşağıda gördüğünüz gibi sanal sayı içeriyor. ( Biraz detay incelemek isterseniz: Schrödinger’in Kedisi Deneyi Neden Yapılmıştı? Schrödinger Denklemi Neyi Kanıtladı?)
Karmaşık sayılar kesinlikle faydalı araçlardır ancak kuantum mekaniğinde karşımıza çıkması aslında bazı fizikçileri rahatsız eder. Matematik tarihine meraklı olanların hatırlayacağı gibi sanal sayılar bir zamanlar matematikçileri de rahatsız etmişti.
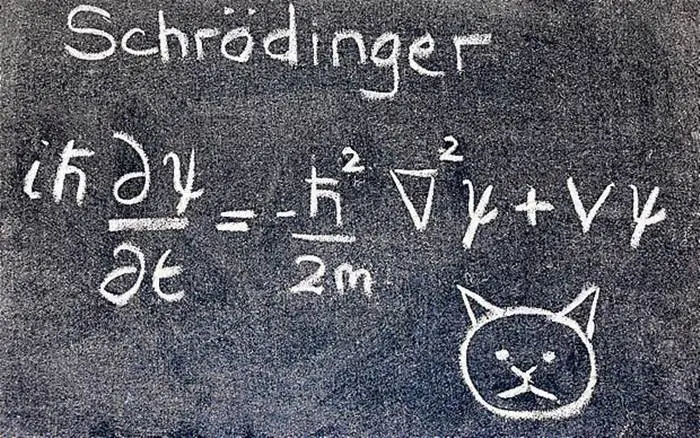
Sanal Sayılar İle Fizikçilerin Sıkıntısı Nedir?
Fizikçi Schrödinger de denklemlerinde karmaşık sayıları kullanmaktan hiç mutlu olmamıştı. Bu sorunu ortadan kaldırmak için de denklemini sadece gerçek sayılarla ifade etmenin alternatif yollarını buldu. Daha sonrasında bazı fizikçiler, “gerçek kuantum mekaniği” adı verilen versiyonlarla sanal sayılardan kaçınarak yani sadece gerçek sayıları kullanarak kuantum teorisi oluşturmaya çalıştılar.
Ancak karmaşık kuantum mekaniğini simüle etmek için gerçek sayıları kullanmak zaman içinde hantal bir çalışma alanı oluşturacaktı. Tamamen gerçek bileşenlerden oluşan denklemler, deneysel anlamda bazı beklenen sonuçları vermeyince sanal sayıların kuantum fiziğinde gerçekten gerekli olup olmadığı veya sadece yararlı bir hesaplama aracı olup olmadığı sorusu kaldı.
Sonucunda gözlemlemesi mümkün olan nicelikler ve olasılık dağılımları, gerçek sayılarla ifade edilmektedir. Ancak temeldeki dalga fonksiyonları ve kuantum durumları genellikle fiziksel olmayan i sayısını, -1’in karekökü içerir. Aynı şekilde işe yarayan tamamen gerçek sayılardan oluşan bir formül bulmak mümkün olabilir mi?

Bu sorunun cevabı ise Bell testi ile cevaplanacaktı. Bu test, 1964’te fizikçi John Bell tarafından kuantum dolanıklığının kuantum teorisi için gerekli olduğunu kanıtlamak için önerilmişti. Bell test deneyinde, dolanık parçacıklar, iki fizikçiye ( A ve B diyelim) gönderilmektedir. Bu kişiler parçacıkları ölçerler ve ölçümleri karşılaştırdıktan sonra, sonuçların ilişkili olup olmadığına bakarlar. ( Detaylar: Nobel Ödülüyle Adını Duyduğumuz Kuantum Dolanıklık Nedir??
Kuantum Fiziği İçin Sanal Sayılar Zorunlu Gibi Gözüküyor
Son önemde yapılan çalışmalar sonucunda kuantum mekaniğinde karmaşık sayılardan kaçış olmadığını kanıtladı. Bell testinin son versiyonunda, işin içine ikinci bir çift parçacık karıştı. Bu ikinci çiftte B’ye ve üçüncü bir kişiye diyelim ki C’ye gönderildi.
Evren, karmaşık sayılara dayalı standart bir kuantum mekaniği ile tanımlansaydı, A ve C’ye ulaşan fotonların dolanık olması gerekmezdi. Ama gerçek sayılara dayalı bir kuantum teorisinde öyle olmalıydı. Araştırmacılar, fotonların durumlarına bakarak, A ve C dedektörlerine ulaşan fotonların durumlarının dolanık olmadığını gördüler. Bu durum da yalnızca karmaşık sayıları kullanan bir kuantum teorisi ile açıklanabilirdi.
Sonuç olarak sanal sayılardan kaçışımız yok gibi gözüküyor. En iyisi direnmek vazgeçmek ve bu gerçeği kabul etmek. Ayrıca göz atmak isterseniz: Kuantum Fiziği Hakkında Yanlış Anlaşılan 7 Şey
Kaynaklar ve ileri okumalar için:
- Imaginary numbers could be needed to describe reality, new studies find; Yayınlanma tarihi: 21 Aralık 2021; Bağlantı: https://www.livescience.com/
- A Visual, Intuitive Guide to Imaginary Numbers; Bağlantı: https://betterexplained.com/
- Imaginary Numbers May Be Essential for Describing Reality; https://www.wired.com/
- Renou, MO., Trillo, D., Weilenmann, M. et al. Quantum theory based on real numbers can be experimentally falsified. Nature 600, 625–629 (2021). https://doi.org/10.1038/s41586-021-04160-4
- Zheng-Da Li, Ya-Li Mao, Mirjam Weilenmann, Armin Tavakoli, Hu Chen, Lixin Feng, Sheng-Jun Yang, Marc-Olivier Renou, David Trillo, Thinh P. Le, Nicolas Gisin, Antonio Acín, Miguel Navascués, Zizhu Wang (王子竹), and Jingyun Fan, Phys. Rev. Lett. 128, 040402 – Published 24 January 2022
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel











Herkese nasip olmayan bir konum ve atmosferde siniz, ben 65 yaşında bir kişiyim imkansızlıklar ve yokluklar la hayatımı geçirdim, eğer dünyaya bir kez daha gelme olanağı olsaydı,hayatımın son gününe kadar matematik ve müzik. den başka hiç bir şeyle uğraşmazdım; bu bilim denizinde ispatlarla
anılmanız temennisi ile saygılar sevgiler.