Herhangi bir haritayı iki rengin birbirine değmeyeceği şekilde boyamak için kullanabileceğiniz en az renk sayısı nedir? Bu soru ilk bakışta oldukça önemsiz bir soru gibi görünecektir. Ancak bu sorunun matematik için inanılmaz derecede önemli teorik ve pratik sonuçları olmuştur. Bu yazıda öncelikle dört renk teoremine sonrasında da sonuçlarına bakacağız.

Dört renk teoreminin ne olduğuna geçmeden önce Sudoku oyununun, bir davette oturma düzenin ve radyo istasyonlarına frekans atamanın ortak noktasının ne olduğunu soralım. Cevap bunların hepsi kendilerine özgü haritalar ile bir biçimde birbirine bağlı olmasıdır. Bu nedenle de hepsi temelinde dört renk teoremi ile ilgilidir.
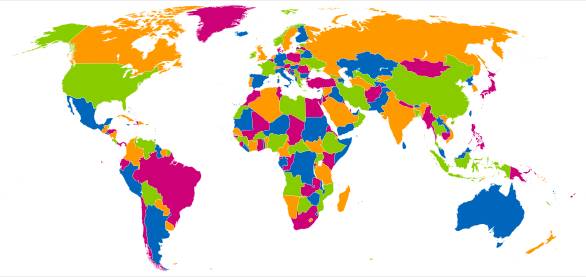
Dört renk teoremi bize herhangi bir haritayı renklendirmek için dörtten fazla renk gerekmeyeceğini söyler. Düzlemsel olmak kaydıyla hangi haritayı boyarsanız boyayın, sadece dört renk yeterli olacaktır. Sadece dört rengi kullanarak, birbirine bitişik bölgelerin farklı renkte olmasını sağlayabilirsiniz. Bunun bir örneğini aşağıdaki dünya haritasında görüyorsunuz.
Dört Renk Teoremi İle Nasıl Tanıştık?
Uzun ve dolambaçlı yolculuk aslında basit bir soru ile başladı. Soru, 23 Ekim 1852’de, Güney Afrikalı bir matematikçi ve botanikçi Francis Guthrie’nin aklına geldi. Kendisi İngiltere haritasını renklendirmeye çalışırken sadece dört farklı renge ihtiyaç duyulduğu fark etmişti. O sırada Guthrie’nin erkek kardeşi de, Londra Üniversitesi’nde ünlü matematikçi August De Morgan’ın öğrencisiydi. Doğal olarak bu soru sonrasında da ona ulaştı.

Ancak mantık konusundaki çalışmaları nedeniyle kendi alanında ünlü biri olan De Morgan bile, soruyu cevaplayamadı. O da soruyu İrlandalı bir matematikçi olan William Hamilton’a sordu. Fakat sorunun cevabını Hamilton da bilmiyordu. Francis Guthrie’nin sorusu şuydu. Her türlü haritanın en fazla dört renk ile boyanacağını ispat etmek mümkün mü?
Dört Renk Teoremini İspat Etme Girişimleri
Zaman içinde bu soru diğer matematikçilerin de ilgi odağına girdi. Francis Galton’un el atmasıyla sorunun şöhreti daha da arttı. Ancak hiç kimse önemli bir ilerleme kaydetmedi. 1878’de, Arthur Cayley (1821-1895), soru ile ilgilenmeye başladı. 1879’da haritaların renklendirilmesi üzerine kısa bir makale yayınladı. Ancak makalesinde bir ispat vermekten ziyade ispat etmenin neden zor olduğunu açıkladı.

Bir ara Cayley’in öğrencisi Alfred Bray Kempe de bir ispat denemesine girişti. Aslında başardı ancak ispatı çok uzundu. Birkaç kişi ikna olsa da genel kabul görmedi. Zaten 10 yıl gibi bir zaman içinde de Percy Heawood, Kempe’nin argümanında bir hatayı bulunca problemin çözüldüğüne dönük hayaller rafa kalktı. Ancak kanıtı yine de ustacaydı ve nihai kanıt için gerekli olan anahtar fikirleri içeriyordu.
Kısacası matematikçiler çok denediler. Çizdikleri her haritayı 4 renge boyayabiliyorlardı. Ama bunu matematiksel olarak kanıtlayamıyorlardı. Aslında bunu yapabilmeleri için 80 yılın daha geçmesi ve süper bilgisayarların yardımı gerekecekti. Ancak ne yazık ki o sıralarda onların bunu bilmesi mümkün olamazdı.
Dört Renk Teoreminin Çözümü Matematik Camiasını Karıştıracaktı
Sonunda Guthrie’nin sorusunu sormasından 124 yıl sonra sorunun çözümü yapıldı. Çözüm 1976 yılında, Illinois Üniversitesi’nde matematikçi olan Kenneth Appel ve Wolfgang Haken’den geldi. Ancak bir sorun vardı. Bu sorunun cevabını IBM 370 bilgisayarlarının yardımıyla bulmuşlardı. Appel ve Hakel yüzlerce sayfa süren bir kanıtla, bu çözüme ulaşmışlardı.
Soru çözülmüştü ama matematikçiler çok da mutlu değildi. Bunun temel nedeni sorunun bir bilgisayar tarafından çözülmesiydi. Bu çözüm geleneksel matematiksel ispat biçiminin dışında kalıyordu. Ayrıca “Kontrol edilebilirlik” sorununu doğuyordu. Sonucunda bu ispatın dayandığı binlerce satırı kimsenin kontrol etmesi olası değildi. Bilgisayar kodlarında hata olağan bir durumdu. Ve böyle bir hata tüm ispatı geçersiz kılabilirdi.
Ancak bu bahanenin arka planında başka temel başka bir neden daha vardı. Matematikçileri cezbeden şey işin bilinmez kısmıydı. Ancak bir makinenin çıkıp size sadece evet cevabını vermesinin güzelliği ve estetiği yoktur. Bugüne kadar dört renk problemini bilgisayar kullanmadan kanıtlayabilen çıkmadı. Matematik dünyası dört renk problemi için hala daha kısa ve geleneksel yapıda bir matematikçinin ispatını bekliyor. Peki ama bunu deneme yanılma yapmadan nasıl başarabiliriz?
Dört Renk Teoremi Çizge Teorisi İle İlişkilidir
Boş bir Türkiye haritanız olduğunu ve bunu elinizdeki renkli kalemler ile boyamak istediğinizi düşünelim. Birbirine karışmaması için her ili farklı renkler ile boyamak isterseniz. Eğer böyle yapmazsanız illerin sınırları birbirine karışacaktır.
Bu problemin nasıl çözüldüğüne anlamak için etraftaki tüm gereksiz bilgiyi kaldırmanız gerekecektir. Yani haritamızdaki illerin isimlerini ve sınırlarını kullanmayalım. Bunun yerine haritadaki her ili bir nokta ile gösterelim. Ve eğer iki il birbirine komşu ise bu illere ait noktalar arasında düz çizgiler çizelim. Bu çizgiler de kenarlarımız olsun. Matematiğe yabancı olmayanlar elde etmek istediğimiz sonucun ne olduğunu anlayacaktır. Çünkü sorumuz harita renklendirme probleminden uzaklaştı. Matematikçilerin “graph theory”i yani graf / çizge teorisi dediği şey ile artık bağlantılı.
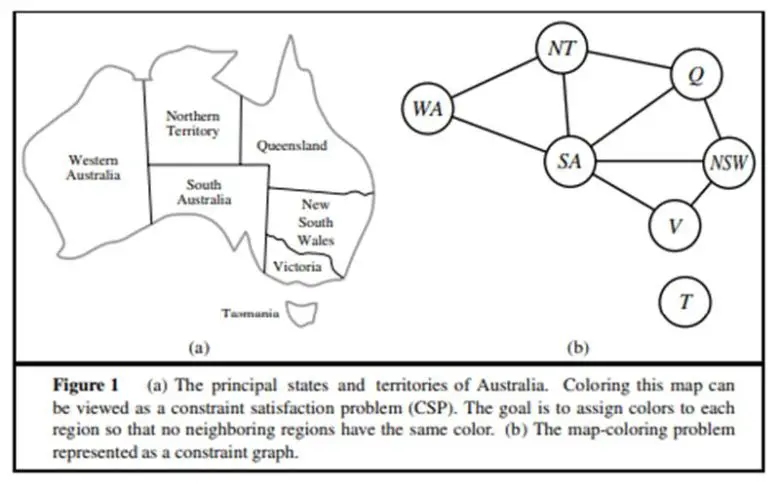
Bu durumda artık sorumuz da değişti. Yeni sorumuz “komşu köşelerin ( illerin) aynı renk olmaması için grafiği dört veya daha az renk ile renklendirebilir miyiz?” biçiminde. Bu durumda nesneler arasındaki ilişkileri incelememize yarayan çizge teorisi yardımı ile soruyu daha kolay bir biçimde ele alabiliriz.
Matematikte graf ya da çizge, düğümler ve bu düğümleri birbirine bağlayan kenarlardan oluşan bir tür ağ yapısıdır. Daha basit konuşmak gerekirse bir graf, köşeler adı verilen sonlu bir nokta kümesinden ve noktaları birleştiren kenarlar adı verilen doğru parçalarından oluşur. Sosyal ağlar, ulaşım ağları veya internet gibi ağlarla çevrili olduğumuz için graf teorisi modern matematikte önemli bir rol oynar.

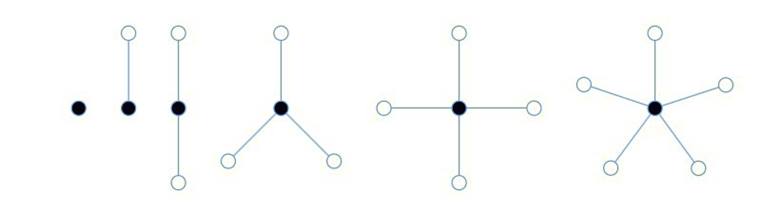
Dört renk teoremi kapsamında da önemli bir sonucu elde ederiz. Hangi harita ile çalışırsak çalışalım bu mantık bize yukarıdaki görselde gördüğünüz gibi eşdeğer şekiller verecektir. Bu mantık ile hareket eden Kempe önemli bir sonuca ulaşmıştı. Ne kadar karmaşık olursa olsun tüm haritalarda 0,1,2,3,4 ya da 5 komşusu olan en az bir bölge bulunuyordu. Kempe, bu fikirden yola çıkarak herhangi bir haritanın dört renkle boyanacağını kanıtladığını sanacaktı.
Sonuç Olarak
Kempe’in kanıtının yanlış olmasına karşın bu kanıtta kullandığı yöntemi teoremin sonunda kanıtlanmasına neden oldu. Ancak yine de Kempe her haritanın beş veya daha az renkle renklendirilebileceğini bizlere göstermişti. Bu önemli bir adımdı ancak 1968 yılına kadar elimizde tam bir kanıt yoktu. Guthrie’nin sorunu ortaya atmasından 124 yıl sonra, 1976’daki bir konferansta Wolfgang Haken, Kenneth Appel ile işbirliği yaparak ve yüksek lisans öğrencisi John Koch’un da yardımıyla bir kanıt duyurdu.

Bu kanıt temel ağ yapılarının tüm kombinasyonlarının ( 1.936 tane) kontrol edilmesi ile yapılmıştı. Bunun için de yaklaşık 1000 saat bir bilgisayardan yardım almışlardı. Bu sayede de sonrasında tartışmalara neden olsa da bilgisayar yardımıyla kanıtlanan ilk matematik teoremi olacaktı.
Kaynaklar ve ileri okumalar:
- The Colorful Problem That Has Long Frustrated Mathematicians. Yayınlanma tarihi: 29 Mart 2023. Kaynak site: Quantamagazine. Bağlantı: The Colorful Problem That Has Long Frustrated Mathematicians
- Myths of maths: The four colour theorem; Yayınlanma tarihi: 23 Mart 2020; Bağlantı: https://plus.maths.org
Matematiksel