Hiçlikten Elde Edilen Sıfır Sayısının Kısa Tarihi

Bir huş ağacı kabuğunun üzerindeki küçük bir nokta, matematik tarihinin en önemli dönüm noktalarından birine işaret ediyor. Bu kabuk, Bakhshali El Yazması olarak bilinen eski bir Hint matematik metnine ait. Üzerindeki küçük nokta ise, sıfır kavramının bilinen ilk yazılı kullanımı olarak kabul ediliyor. Bu yazıda, başlangıçta bir sayı olarak bile görülmeyen, kimi zaman uğursuz sayılan, kimi zaman hayranlık uyandıran sıfırın ilginç tarihini anlatacağız.

Bilgi birikimimizde bazı unsurlar vardır ki, onları sorgulamadan kabul ederiz. Günlük hayatımızda sık sık kullanırız ve yaşamımızı sürdürebilmemizde son derece başarılı olmuşlardır. Sıfırı içeren sayı sistemi de bunlardan biridir. Ancak sıfır her zaman var olmamıştı. Bu kavram, insanlık saymayı öğrendikten sonra geliştirdiği dahiyane bir icattır.

Sıfırın Tarihi Sıfıra ihtiyaç Duyulmayan Bir Dünyada Başladı

Bugün sıfır olmadan matematiği düşünmek neredeyse imkânsız. Kullandığımız ondalık sistem gibi konumlu sayı sistemlerinde, bir rakamın bulunduğu yer büyük önem taşır. Örneğin, 100 ile 1.000.000 arasındaki gerçek fark, 1 rakamının nerede durduğuyla ilgilidir ve bu ayrımı mümkün kılan şey sıfırın varlığıdır.

Ancak binlerce yıl boyunca insanlar sıfır olmadan yaşadı. Antik Sümerli katipler, bir şeyin yokluğunu belirtmek için boşluklar kullanıyordu. Babilliler ise büyüklükleri ayırt etmek için iki küçük kamadan oluşan bir işaret kullanıyordu (tıpkı bugün ondalık sistemimizde sıfırları kullanarak onlar, yüzler gibi değerleri ayırt ettiğimiz gibi). Mayalar da takvimlerinde benzer şekilde bir boşluk belirteci kullanmışlardı.

Ancak tüm bu uygarlıklar sıfırı bir yer tutucu olarak düşünmüşlerdir. Beşinci yüzyılda Hindistan’ın sayı sistemi, sıfırı bir sayı olarak kullanan ilk sistem oldu. Hindistan’ın Gwalior kentindeki bir tapınağın duvarında bulunan ve bir sıfırı andıran daire şekli, dünyanın bilinen en eski sıfır temsili olarak kabul edilir.

MS 628’de, Rajasthan’daki bir dağda yaşayan bir Hintli bilge, dünyanın en önemli matematiksel keşiflerinden birini yaptı. Büyük matematikçi Brahmagupta (598-670), hiçlik ve boşluk hakkındaki Hint felsefi fikirlerini araştırdı ve sıfır kavramını tanımlayan bir inceleme ortaya koydu.

Sıfır, onun döneminde zaten var olan bir kavramdı. Ancak Brahmagupta, sıfırı yalnızca bir sembol ya da boşluk olarak değil, bağımsız bir sayı olarak ele aldı ve ona matematiksel bir kimlik kazandırdı. Sıfır ile işlem yapma kurallarını ilk kez sistematik olarak tanımladı.

Sıfır Matematik Tarihine Neden Bu Kadar Geç Girdi?

Sıfırın matematik tarihine geç gelmesi, kısmen bazı kültürlerin “hiçlik” kavramına duyduğu olumsuz bakış açısının bir yansımasıydı. Batı felsefesi uzun süre boyunca hiçlik kavramı ve dilin mistik gücü konusunda ciddi yanlış anlamalarla uğraştı. MÖ 5. yüzyılda yaşayan Yunan filozof Parmenides, “hiçlik” diye bir şey olamayacağını, çünkü bir şeyden söz edebilmenin, onun var olması gerektiği anlamına geldiğini ileri sürdü. Bu Parmenidesçi bakış açısı, yüzyıllar boyunca birçok düşünürü meşgul etti.

Hristiyanlığın ortaya çıkışından sonra ise, Avrupa’daki dini liderler, Tanrı’nın her şeyde mevcut olduğuna inandıkları için, “hiçlik” kavramını şeytani bir unsur olarak gördüler. İnsanı şeytandan koruma adına sıfır kavramı yasaklandı. Ancak buna rağmen, tüccarlar sıfırı gizlice kullanmaya devam etti.

Buna karşılık Budizm’de “hiçlik” kavramı, şeytani bir anlam taşımaz. Tam tersine, nirvanaya ulaşma yolunda derinlemesine incelenmesi gereken merkezi bir fikir olarak kabul edilir. Bu bakış açısıyla, “hiçliği” matematiksel olarak temsil edecek bir sembol oluşturmak, herhangi bir sorun teşkil etmedi. Zaten İngilizce’deki “zero” kelimesi de, kökenini Sanskritçe ve Hintçedeki “sunyata” kelimesinden alır. Sunyata, “hiçlik” anlamına gelir ve Budist felsefenin temel kavramlarından biridir.

Sıfır Sayısının Dünyaya Yayılışı

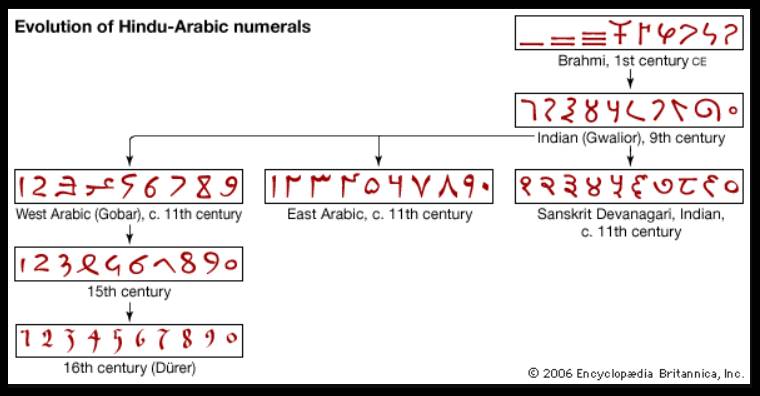
8. yüzyılda İslam, Hindistan’ın bazı bölgelerine yayılmıştı. Bu durum, Hintli matematikçilerin sıfır kavramı da dahil olmak üzere bilgilerini Arap dünyasındaki alimlerle paylaşmalarına zemin hazırladı. MS 9. yüzyılın başlarında El-Harizmi, Bağdat’taki ünlü Bilgelik Evi’nde baş astronom ve kütüphaneci olarak görev yapıyordu.

Burada eski Yunanlılar ve Hindulara ait bilimsel ve matematiksel el yazmaları üzerinde çalıştı. Daha sonra yazdığı “Hindistanlıların Hesap Sanatı” adlı eserinde, 10 rakama dayanan Hint sayı sistemini ayrıntılı biçimde tanımladı.

Orta Çağ’da Avrupalılar hâlâ Roma rakamlarını kullanarak işlemlerini yürütüyordu. Ancak İpek Yolu gibi ticaret yolları sadece baharat ve kumaş taşımadı. Aynı zamanda bilgiyi de Batı’ya aktardı. İtalyan bir tüccarın oğlu olan Fibonacci, babasının işi nedeniyle sık sık seyahat etti. Kuzey Afrika’da bulunduğu sırada, Arap tüccarların 1’den 9’a kadar rakamlar ve sıfırla çalışan çok daha pratik bir muhasebe sistemi kullandıklarını keşfetti.

Fibonacci, bu yeni sayı sisteminin Avrupa’da defter tutma ve muhasebeyi köklü biçimde geliştirebileceğini hemen fark etti. 1202 yılında, bu sistemi tanıtmak amacıyla Liber Abaci (Hesap Kitabı) adlı eserini yayımladı.

Sıfır Sayısının İcadı Kolay Kabul Görmedi

Ancak Roma rakamlarıyla büyümüş olan Avrupa halkı, sıfır kavramına karşı temkinlilik gösterdi. Brçok kişi, sıfırı hem pratik hem de felsefi açıdan şüpheyle karşıladı.

Örneğin, 1299 yılında İtalya’nın Floransa kentinde Arap rakamlarının, özellikle de sıfırın kullanımı yasaklanmıştı. Bu yasak, ticarette alışılmadık rakamların kullanımının kargaşaya neden olabileceği endişesiyle getirilmişti.

1500’lü yıllarda bile bu durum değişmedi. İtalyan bilgin Gerolamo Cardano, sıfır kullanmadan ikinci dereceden ve kübik denklemleri çözüyordu. Avrupalılar ancak 1600’lü yıllarda, İngiliz matematikçi John Wallis’in sıfırı sayı doğrusuna dahil etmesiyle sıfırı kabul etmeye başladı.

Sıfırın icadı, kesirleri tanımlamak için yeni ve çok daha hassas bir yöntem de sağladı. Bir sayının sonuna sıfır eklemek, büyüklüğünü artırırken; ondalık noktasının soluna sıfır eklemek, büyüklüğünü azaltır. Ondalık noktasının sağına sonsuz sayıda basamak eklemek ise sonsuz bir hassasiyet sağlar.

Bu tür bir hassasiyet, 17. yüzyılda Isaac Newton ve Gottfried Leibniz’in sürekli değişimi inceleyen kalkülüsü geliştirmeleri için tam da ihtiyaç duydukları şeydi. Sonuç olarak, modern matematiğin temelleri, aslında “hiçlik” için geliştirilmiş bir gösterim biçiminin ürünüdür.

Kaynaklar ve İleri okumalar:

• Who invented the zero? Yayınlanma tarihi: 22 Ocak 2014; Kaynak site: History. Bağlantı: Who invented the zero?
• Who Invented Zero?; yayınlanma tarihi: 18 Eylül 2017; Kaynak site: Live Science. Bağlantı: Who Invented Zero?
• Aczel M, Aczel D and Ville M (2019) Hero From the East. How Zero Came to the West. Front. Young Minds. 7:128. doi: 10.3389/frym.2019.00128
• Nothing matters: how the invention of zero helped create modern mathematics. Yayınlanma tarihi:20 Eylül 2017. Kaynak site: Conversation. Bağlantı: Nothing matters: how the invention of zero helped create modern mathematics

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel